(1) The degree of p(λ) is exactly n.
(2) p(λ) has at most n roots.
Assume, further, that p(λ) factors in the following form:
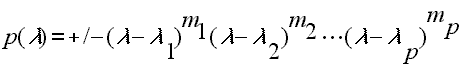
where the λi's are distinct. [Recall, mi is called the multiplicity of λi.]
The Big Eigenvalue - Eigenvector Theorem
Definition: An nxn matrix A is said to be diagonalizable if there exists an nxn diagonal matrix D and an nxn invertible matrix P such that A = PDP-1 .
Theorem: An nxn matrix A is diagonalizable if and only if Rn has a basis of eigenvectors of A, and, in fact, when this happens, if we set P to be the matrix whose columns are these eigenvectors and D the diagonal matrix whose entries are the corresponding eigenvalues, then A = PDP-1 .
Theorem: [The Big Eigenvalue - Eignevector Theorem]
Let A be an nxn matrix.
Let p(λ) = det (A - λI). That is, p(λ) is the characteristic polynomial of A.
Then λ
(1) The degree of p(λ) is exactly n.
(2) p(λ) has at most n roots.
Assume, further, that p(λ) factors in the following form:
where the λi's are distinct. [Recall, mi is called the multiplicity of λi.]
Then
(3) m1 + m2 + ... + mp = n
(4) p = n if and only if each mi = 1, and in this case A is diagonalizable. In fact, if vi is an eigenvector of λi, and if we set P to be the nxn matrix whose columns are these vi's and if we set D to be the nxn diagonal matrix whose diagonal entries are the λi's, then, A = PDP-1. [Recall, that if a collection of eigenvectors have distinct eigenvalues, then they are linearly independent.]
(5) dim {v | Av = λiv } < mi, for each i. [Recall: {v | Av = λiv } is called the eigenspace of vi.]
(6) A is diagonalizable
if and only if
dim (eigenspace of vi ) = mi for EACH i.
if and only if
the sum of the dimension of the eigenspaces of A = n
AND, in this case a basis of Rn which are eigenvectors for A can be constructed by finding a basis for each eigenspace of A and combining (taking the union of) these eigenvectors to form one large set. Furthermore, the P and D in the formula A = PDP-1 are found as follows: P is the matrix whose columns are that basis of eigenvectors of Rn and D is the diagonal matrix which has m1 copies of λ1, , m2 copies of λ2, ...., mp copies of λp.
A Useful formula: If a matrix is triangular (that is, is either filled with zeros below the main diagonal or filled with zeros above the main diagonal) then its determinant is the product of the diagonal entries of this matrix.