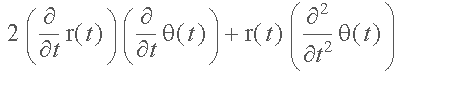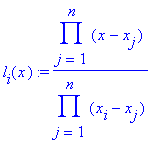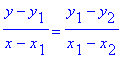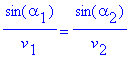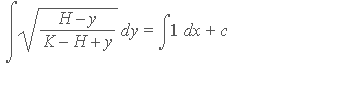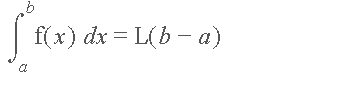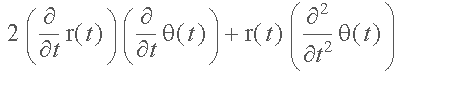Special Problems

How to Write These Up: Carefully!  That is: use those helper words: Let, so, but, thus, so we know, now we prove, we must show, it thus follows from, etc.  REMEMBER: you are to take the position that you have discovered something and are tell me (an intelligent reader!) what the solution is.  But, I'm not clairvoyant, so you need to work hard and write carefully so that I can understand your argument. NOTE: I've renumbered these.

SP #1: This problem is motivated by the Paint Paradox:  Recall, in that problem, that one of the steps was to show that the area under y=1/x from 1 to infinity was infinite.  This problem asks you to figure out what happens when y=1/x is replaced by y=1/x^r for various r real numbers r.  [Of course, r is the exponent of x, using the convention that "^" means "raise to."]  Specifically, show the following:

  Theorem: Let y=1/x^r, where r is a real number.  Then

    (a) If r > 1, then the area under y=1/x^r from 1 to infinity is finite.  [Actually find this area in terms of r.]

    (b) If r < 1, then the area under y=1/x^r from 1 to infinity is infinite.

  COMMENTS:

(1) Of course, by the area from 1 to infinity, one means the limit as t approaches infinity of the area from 1 to t. 

(2) We will see an application of this theorem when we do Chapter 11, Infinite Series.  There is a test, called the Integral Test, that uses this result.

SP #2: I forgot.  Maybe it was to prove the reduction formula #74 at the back of the book.

SP# 3: In the proof of Theorem B in the section on numerical integration, we were trying to show that f(b)=f(a)+f '(a)(b-a)+f ''(c)/2 [b-a]^2 for some c in (a,b).  To this end, we defined L by the equation: f(b)=f(a)+f '(a)(b-a)+L[b-a]^2 and defined p(t)=f(b)-f(t)-f '(t)(b-t)-f ''(c)/2 [b-t]^2.  In SP #2, you are to: 
     (a) Show p(a)=0
     (b) Show p(b)=0
     (c) Use the Mean Value Theorem applied to p(t) and (a) and (b) above to find L.

SP #4: Show Theorem B + Theorem C implies Theorem A of the numerical integration section.  Hint: Write f(x)=f(a)+f '(a)(x-a)+f ''(c(x))/2 [x-a]^2 (which follows is just Theorem B), and integrate this from a to b and then use Theorem C to help evaluate one of the integrals you get.

SP #5: In the Gaussian Quadrature section, let (x₁, y₁), (x₂, y₂), .... (x_n, y_n) be points in the plane with the x_i's all disctinct real numbers.  Define l_i(x) as the product below, where the products are taken over all j except j=i.  Notice that each  l_i(x) is a polynomial in x of degree n-1.

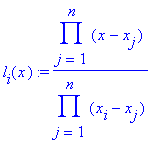
A. Show l_i(x_j)= 1 if i=j and 0 otherwise

B. Set P(x) = y₁l₁(x) + ... + y_nl_n(x).  Show P(x) is a polynomial of degree < n-1 which passes through each of the n points (x₁, y₁), (x₂, y₂), .... (x_n, y_n).

C.  Show that if Q(x) is any other polynomial of degree <  n-1 passing through these same n points, then P(x)=Q(x), so that P(x) is the UNIQUE polynomial of degree < n-1 passing through these n points. [HINT: you'll need the result that a polynomial of degree n has at most n roots.  Also, recall, we said in class that a polynomial of degree n with complex  (or real) coefficients has exactly n roots, if they are counted "properly."  MORE HINT: Let H(x)=P(x)-Q(x) and show H(x)=0 by showing it has more roots than it "should."]

D.  If n=2, show that P(x) becomes the following two-point formula for the equation of a line:

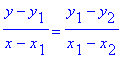
SP #6 [Thanks to Victor].  How can Simpson's rule give the exact answer for lines (it is actually supposed to give the exact answer  for cubic and lower degree polynomials) when it approximates functions by parabolas and a line is straight?  Suggestion:  Look at the line y=mx and the interval [a,b].   Find the parabola passing through the three points [a,ma], [(a+b)/2), m(a+b)/2], and [b, mb] and discover why the area under this parabola is indeed the area under the line [from x=a to x=b].

SP #7 Open that Maple worksheet [that I e-mailed you already] called gauss.mws [you may have to SHIFT-CLICK to let you save it to disk] and use it to look at the roots various different Legrendre polynomials, and make then some guesses (conjectures) about the location (distribution) of these roots.

SP #8A Snell's Law.  In the picture below, show that the value of x that minimizes the time for an object to travel from point P to point Q such that 

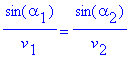
where a₁ and a₂ are the angles between the vertical yellow line and the green and red lines, respectively, and v₁ and v₂ are the velocities above and below the blue line, respectively.

 P

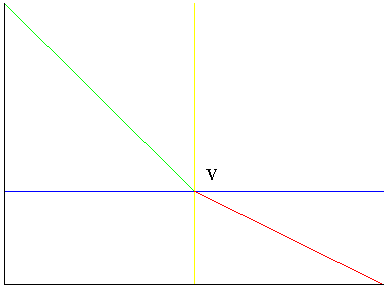
                                               x                                             Q

HINT: Find, in terms of x, the the total time to travel from P to Q through V by finding (in terms of x), the time to travel from P to V and adding to that the time to travel from V to Q.  Call that function T(x). Then use calculus to find a condition for T(x) to be a minimum.  When you do, out will pop Snell's Law.

SP #8B: [The Brachistochrone Problem: This is the end of the argument that a bead sliding down a frictionless wire from a point (0,H) does so in minimal time when the shape of the curve it is sliding down is a cycloid.

We had derived a differential equation for y=f(x), the equation of this path of least time and found that:

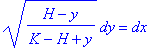for some constant K.

In this problem, you will integrate this expression and then recognize it (somehow) as a cycloid).

A.  First, integrate both sides, getting

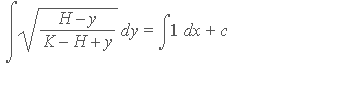
and then make two changes of variables: First, set v=H-y and then set
tan (f) = sqrt(v/(K-v).  [You'll need to show that v = K sin² (f) to find dv.]

B. Then do the integral [it will be one with respect to f.] you get and show
K(f - (1/2) sin 2f) = -x + C₁, where C₁ is another constant.

C.  Use the fact that tan (f) = sqrt(v/(K-v), and v=H-y and the fact that the curve passes through the point (0,H) to show that the constant C₁ equals 0.

D.  Use the fact that v = K sin² (f) and v=H-y to show y=H-(K/2)[1-cos 2(f)]

E.  Replace (2f) with q to conclude (show why) that a parametric equation for the curve we are looking for is

x = L (q  - sin(q)) and
y= H - L (1 - cos(q )), for some constant L >0.

F.  Show why THAT is indeed a cycloid.  [You'll need to understand what the "H" is doing in the equation for y and what that minus sign is doing there.]  HINT: Do an example to see what is going on here.  Specifically, you know that

x = t
y = t²

is a parabola.   Now graph

x = t
y = 3 - t²

and see what happens.

SP #9:  Consider the circle in polar form r=2cos(q) and show that the slope of the tangent line to this curve at the point (r,q,) as computed by the formula on page 665 gives the same result as when one first finds the slope of line joining the center of the circle, (1,0), with the the point (r,q) [you'll need to change this to rectangular coordinates to find that slope] and then taking the negative reciprocal of that slope.

SP #10: Assume we have n vectors ·  in n-space which satisfy:

(1) v_i · v_i= 1 for i=1,...n..

(2) v_i · v_j = 0  if i does not equal j.

 

[Recall that this means that the vectors  v₁, ._.. ,v_n are a "coordinate system," in that each has unit length and that are perpendicular.  Recall, further, that the "dot" product of two vectors is the sum of the products of their coordinates.  That is:
(u₁, ..., u_n) · (v₁, ..., v_n) = u₁v₁+... +u_nv_n ]

 

Now, let F=(x₁, ..., x_n) be any vector in n-space.

 

Show:   F= (F · v₁)v₁ +(F· v₂)v₂.... + (F · v_n)v_n

 

NOTE: Recall the following definitions of vector addition and scalar multiplication.

 

(a)  (u₁, ..., u_n) + (v₁, ..., v_n) = (u₁+v₁, ..., u_n+v_n)

(b) K (u₁, ..., u_n) = (Ku₁, ..., Ku_n), for any constant (scalar) K.

NOTE: What this problem does is to give a formula for the coordinates of a vector F with respect to a new coordinate system.

 

SUGGESTION:  Do the case n=2 first.

 

RECALL: We needed this result to find the components of gravity in the r-direction and the theta-direction.  Here is the Maple worksheet that used this idea:

kepler_for_class.mws.

 

HINTS:

A.  You may find useful the following properties of dot product.  You may simply use them but it would be better if you were to prove them:

(1) If u, v and w are vectors in n-space, then u·(v+w) = u·v + u·w

(2) If u and v are vectors in n-space and K is a number, then u·(Kv) = K (u·v)

(3) If u is a vector in n-space and if v₁, ._.. ,v_n are as in this problem and
      if u·v_i = 0 for i=1, 2, ..., n, then u = 0. 

[Comment: (1) and (2) are easy to prove but (3) is not so easy.  The proof of (3) is usually given in a linear algebra class such as Math 203 or 322 (or 321?)]

 

B.  This problem really approached two ways: 

(1) A PARTIAL SOLUTION: Show that if F = c₁v₁ +c₂v₂.... + c_nv_n then c_i=F· vi for each i. [This part is "straightforward" and does not use Hint A (3), above.]  [The point is that we actually have no a priori reason to thing that F is a combination of the v_i's, but if we assume it is, then it is not so hard to find out those coefficients, c_i.

 

(2) A FULL SOLUTION: Show that 
F - [ (F · v₁)v₁ +(F· v₂)v₂.... + (F · v_n)v_n ]=0 by a direct application of Hint A (3) above.

SP #11:  Let f(x) be a function.

Assume there exists a constant, L, such that for all real number a and b, we have:

 

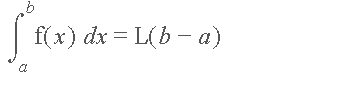
Show: f(x) = L (that is, that f(x) is the constant function L)

 

HINT:  Apply the hypothesis with a=a and b=t, with t a variable.  The differentiate both sides and use the Fundamental Theorem of Calculus.

 

NOTE: Of course, the converse is true:  if f(x) does = L, then that integral formula is certainly true.

 

NOTE: We needed this fact to show that r(t)² dq/dt is constant and we needed THIS to show that the  q-component of gravity (below) equals 0, and THIS was the case because the derivate of  r(t)² dq/dt had to be 0 (since it is constant) and this derivative is this q-component of gravity time r(t), but r(t) is not zero so the q-component of gravity is zero (whew!!).