Image compression is made possible using the concept of orthogonality. Using a process called the discrete cosine transform, one can carry out a least squares approximation on an image, thus reducing the number of bits needed to store it. This process is known as lossy compression, and therefore results in some loss of clarity, but it is generally kept to a threshold that is either imperceptible or considered tolerable to the human eye.
Considering this project involved JPEG compression, I figured this was a great opportunity to play with an image of one of my favorite artists, JPEGMAFIA. (JPEG, or Peggy, for short.)


Problem 3 called for manipulating a black and white image, leaving manipulation of color images for later problems. First, I read in the the file using imread and converted it to double type for increased accuracy. Next, I found an 8x8 square to use for initial testing. One speed bump I ran into was initially choosing a square that had too little going on. It was mostly dark-colored squares, so compressing it yielded an almost totally black image with little progression between different levels of compression. I found that a square in the patch of grass on JPEG's left worked best.
1234567% Problem 3
x = imread('peggy_bw.jpeg');
x=double(x);
%% part a
xb=x(500:507,600:607)
figure(1)
imagesc(xb);colormap(gray)
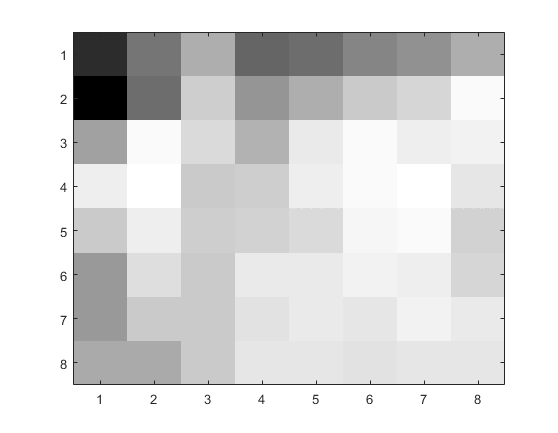
Next, I built the matrix and applied the 2D-DCT to the 8x8 section of the image and stored it as the matrix . Using this , I quantized the image using , dequantized the image, then applied the reverse 2D-DCT to reconstruct the image. I repeated this process for values of 2 and 4.
1234567891011121314151617181920212223%% part b: apply the 2d-dct
n=8
for i=1:n
for j=1:n
C(i,j)=cos((i-1)*(2*j-1)*pi/(2*n));
end
end
C=sqrt(2/n)*C;
C(1,:)=C(1,:)/sqrt(2);
xb = xb-128;
Y=C*xb*C';
%% parts c and d
% p=1
p=1; % changed to 2 and 4, respectively, for other two trials
Q=p*8./hilb(8);
Yq=round(Y./Q)
% dequantization step
Ydq=Yq.*Q;
Xdq=C'*Ydq*C; % inverse dct
Xe=Xdq+128;
Xf=uint8(Xe);
figure(2)
imagesc(Xf);colormap(gray)
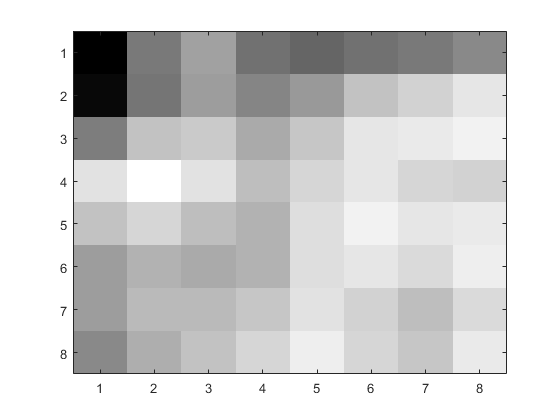
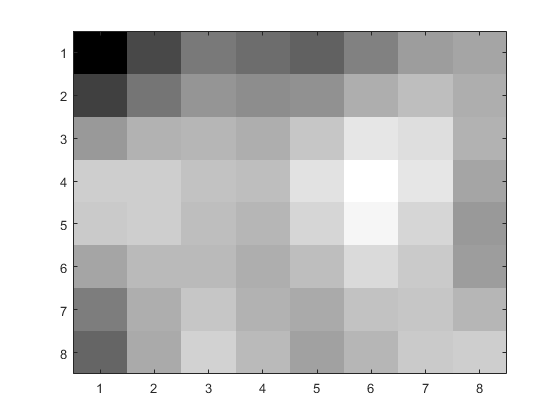
Once I did that for the single 8x8 block, I repeated the process for the whole image.
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657%% part e
p1mat = zeros(640,640);
p2mat = zeros(640,640);
p4mat = zeros(640,640);
for row=1:8:639
for col=1:8:639
xb=x(row:row+7,col:col+7);
%% part b: apply the 2d-dct
n=8;
for i=1:n
for j=1:n
C(i,j)=cos((i-1)*(2*j-1)*pi/(2*n));
end
end
C=sqrt(2/n)*C;
C(1,:)=C(1,:)/sqrt(2);
xb = xb-128;
Y=C*xb*C';
%% parts c and d
% p=1
p=1;
Q=p*8./hilb(8);
Yq=round(Y./Q);
% dequantization step
Ydq=Yq.*Q;
Xdq=C'*Ydq*C; % inverse dct
Xe=Xdq+128;
Xf=uint8(Xe);
p1mat(row:row+7,col:col+7)=Xf;
% p=2
p=2;
Q=p*8./hilb(8);
Yq=round(Y./Q);
% dequantization step
Ydq=Yq.*Q;
Xdq=C'*Ydq*C; % inverse dct
Xe=Xdq+128;
Xf=uint8(Xe);
p2mat(row:row+7,col:col+7)=Xf;
% p=4
p=4;
Q=p*8./hilb(8);
Yq=round(Y./Q);
% dequantization step
Ydq=Yq.*Q;
Xdq=C'*Ydq*C; % inverse dct
Xe=Xdq+128;
Xf=uint8(Xe);
p4mat(row:row+7,col:col+7)=Xf;
end
end
figure(1)
imagesc(p1mat);colormap(gray)
figure(2)
imagesc(p2mat);colormap(gray)
figure(3)
imagesc(p4mat);colormap(gray)



Problem 4 called for essentially the same process as Problem 3 but using the JPEG-suggested matrix for quantizing and using . Put another way, I did the same thing as Part E in the last problem, except with a constant matrix instead of computing it during the quantization phase.
1234567891011121314151617181920212223242526272829303132333435363738% Problem 4
Q = [
16 11 10 16 24 40 51 61;
12 12 14 19 26 58 60 55;
14 13 16 24 40 57 69 56;
14 17 22 29 51 87 80 62;
18 22 37 56 68 109 103 77;
24 35 55 64 81 104 113 92;
49 64 78 87 103 121 120 101;
72 92 95 98 112 100 103 99;
];
p1mat = zeros(640,640);
for row=1:8:639
for col=1:8:639
xb=x(row:row+7,col:col+7);
n=8;
for i=1:n
for j=1:n
C(i,j)=cos((i-1)*(2*j-1)*pi/(2*n));
end
end
C=sqrt(2/n)*C;
C(1,:)=C(1,:)/sqrt(2);
xb = xb-128;
Y=C*xb*C';
% p=1
p=1;
Yq=round(Y./Q);
% dequantization step
Ydq=Yq.*Q;
Xdq=C'*Ydq*C; % inverse dct
Xe=Xdq+128;
Xf=uint8(Xe);
p1mat(row:row+7,col:col+7)=Xf;
end
end
figure(4)
imagesc(p1mat);colormap(gray)

Problem 5 called for the same steps as Problem 3 except with a color image instead of a black and white one. While the process is much the same, using RGB instead of a simple black/white value means I had to process the R, G, and B values individually and recombine them into a single image in the end.
First, like in Problem 3, I imported the image and focused on an 8x8 square. This time, however, I also had to separate the imported matrix into separate R, G, and B matrices.
12345x=imread('peggy.jpeg');
x=double(x);
%% part a
xb=x(500:507,600:607,:);
r=xb(:,:,1);g=xb(:,:,2);b=xb(:,:,3);
Next, the process was again much the same as in Problem 3, just that the process done for just xb before then had to be done for R, G, and B.
1234567891011121314151617181920212223242526272829303132333435363738394041%% part b: apply the 2d-dct
n=8
for i=1:n
for j=1:n
C(i,j)=cos((i-1)*(2*j-1)*pi/(2*n));
end
end
C=sqrt(2/n)*C;
C(1,:)=C(1,:)/sqrt(2);
r = r-128;
g = g-128;
b = b-128;
Yr=C*r*C'
Yg=C*g*C'
Yb=C*b*C'
%% parts c and d
% p=1
p=1;
Q=p*8./hilb(8);
Yqr=round(Yr./Q)
Yqg=round(Yg./Q)
Yqb=round(Yb./Q)
% dequantization step
Ydqr=Yqr.*Q;
Ydqg=Yqg.*Q;
Ydqb=Yqb.*Q;
Xdqr=C'*Ydqr*C; % inverse dct
Xdqg=C'*Ydqg*C; % inverse dct
Xdqb=C'*Ydqb*C; % inverse dct
Xer=Xdqr+128;
Xeg=Xdqg+128;
Xeb=Xdqb+128;
Xfr=uint8(Xer);
Xfg=uint8(Xeg);
Xfb=uint8(Xeb);
figure(4)
imagesc(Xfr);colormap(autumn)
figure(5)
imagesc(Xfg);colormap(summer)
figure(6)
imagesc(Xfb);colormap(winter)
Finally, like before, I extended this process to the entire image.
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677 %% part e
rmat = zeros(640,640);
gmat = zeros(640,640);
bmat = zeros(640,640);
for row=1:8:639
for col=1:8:639
xb=x(row:row+7,col:col+7,:);
r=xb(:,:,1);g=xb(:,:,2);b=xb(:,:,3);
%% part b: apply the 2d-dct
n=8;
for i=1:n
for j=1:n
C(i,j)=cos((i-1)*(2*j-1)*pi/(2*n));
end
end
C=sqrt(2/n)*C;
C(1,:)=C(1,:)/sqrt(2);
r = r-128;
g = g-128;
b = b-128;
Yr=C*r*C';
Yg=C*g*C';
Yb=C*b*C';
%% parts c and d
% p=1
p=8;
Q=p*8./hilb(8);
Yqr=round(Yr./Q)
Yqg=round(Yg./Q)
Yqb=round(Yb./Q)
% dequantization step
Ydqr=Yqr.*Q;
Ydqg=Yqg.*Q;
Ydqb=Yqb.*Q;
Xdqr=C'*Ydqr*C; % inverse dct
Xdqg=C'*Ydqg*C; % inverse dct
Xdqb=C'*Ydqb*C; % inverse dct
Xer=Xdqr+128;
Xeg=Xdqg+128;
Xeb=Xdqb+128;
Xfr=uint8(Xer);
Xfg=uint8(Xeg);
Xfb=uint8(Xeb);
rmat(row:row+7,col:col+7)=Xfr;
gmat(row:row+7,col:col+7)=Xfg;
bmat(row:row+7,col:col+7)=Xfb;
end
end
% rgb images
r=x(:,:,1);g=x(:,:,2);b=x(:,:,3);
% figure(1)
% imagesc(r);colormap(autumn)
% figure(2)
% imagesc(g);colormap(summer)
% figure(3)
% imagesc(b);colormap(winter)
% figure(4)
% imagesc(rmat);colormap(autumn)
% figure(5)
% imagesc(gmat);colormap(summer)
% figure(6)
% imagesc(bmat);colormap(winter)
% complete images
rgb=zeros(640,640,3);
rgb(:,:,1)=r;
rgb(:,:,2)=g;
rgb(:,:,3)=b;
rgb=uint8(rgb);
figure(7)
imagesc(rgb);
rgbmat=zeros(640,640,3);
rgbmat(:,:,1)=rmat;
rgbmat(:,:,2)=gmat;
rgbmat(:,:,3)=bmat;
rgbmat=uint8(rgbmat);
figure(8)
imagesc(rgbmat);


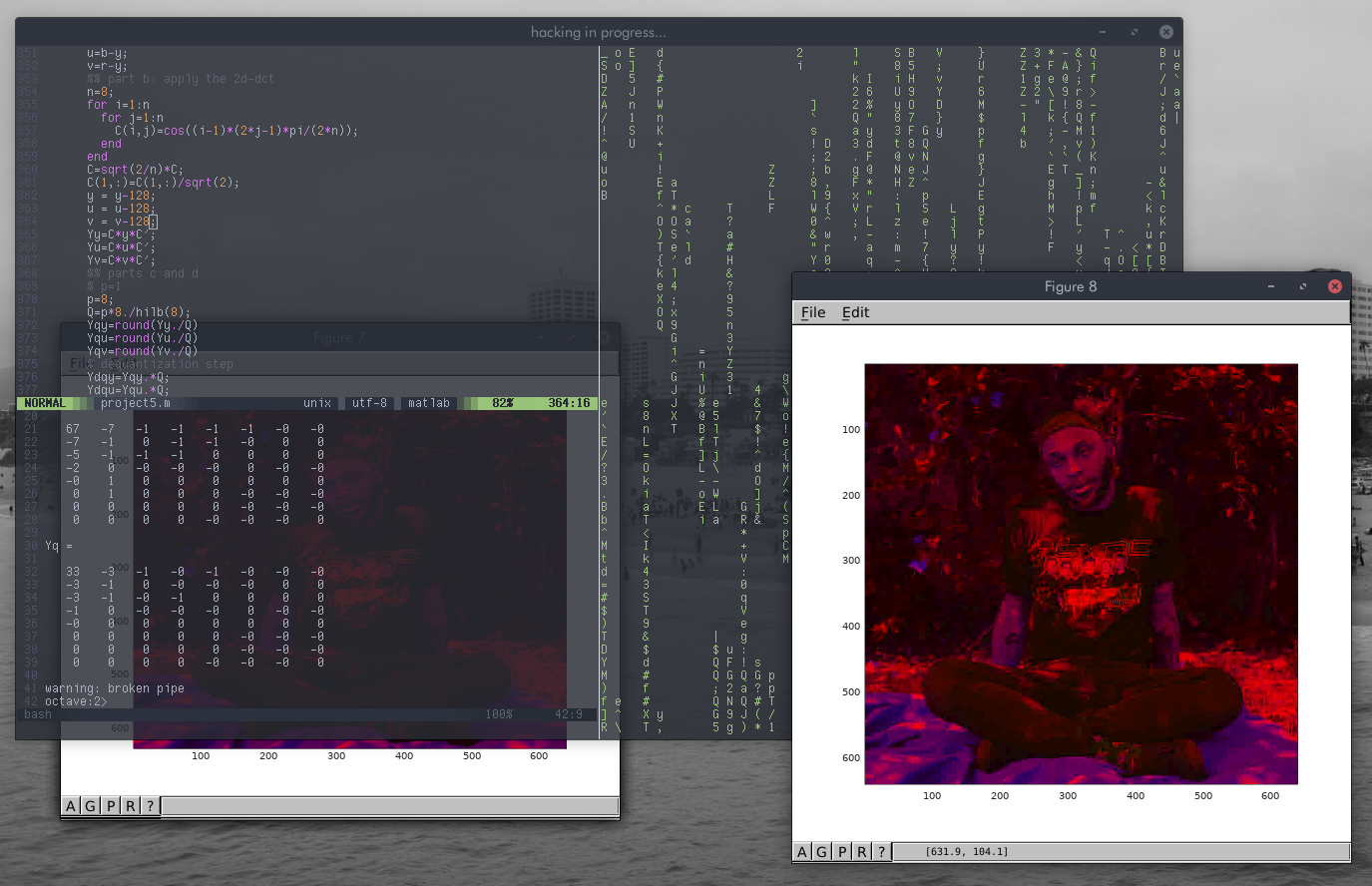
Problem 6 calls for much the same process as in Problem 5, except using YUV instead of RGB. Rather than referring to different levels of colors, YUV instead refers to luminance and color difference. Luminance is defined as , and the color differences are and . I used these values just as I used the RGB values in the last problem. In the end, however, I had to convert them back to RGB to get the proper image.
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139 % Problem 6
x=imread('peggy.jpeg');
x=double(x);
%% part a
xb=x(500:507,600:607,:);
r=xb(:,:,1);g=xb(:,:,2);b=xb(:,:,3);
y=0.299*r+0.587*g+0.114*b;
u=b-y;
v=r-y;
% figure(1)
% imagesc(y);
% figure(2)
% imagesc(u);
% figure(3)
% imagesc(v);
%% part b: apply the 2d-dct
n=8
for i=1:n
for j=1:n
C(i,j)=cos((i-1)*(2*j-1)*pi/(2*n));
end
end
C=sqrt(2/n)*C;
C(1,:)=C(1,:)/sqrt(2);
y = y-128;
u = u-128;
v = v-128;
Yy=C*y*C'
Yu=C*u*C'
Yv=C*v*C'
%% parts c and d
% p=1
p=1;
Q=p*8./hilb(8);
Yqy=round(Yy./Q)
Yqu=round(Yu./Q)
Yqv=round(Yv./Q)
% dequantization step
Ydqy=Yqy.*Q;
Ydqu=Yqu.*Q;
Ydqv=Yqv.*Q;
Xdqy=C'*Ydqy*C; % inverse dct
Xdqu=C'*Ydqu*C; % inverse dct
Xdqv=C'*Ydqv*C; % inverse dct
Xey=Xdqy+128;
Xeu=Xdqu+128;
Xev=Xdqv+128;
Xfy=uint8(Xey);
Xfu=uint8(Xeu);
Xfv=uint8(Xev);
figure(4)
imagesc(Xfy);
figure(5)
imagesc(Xfu);
figure(6)
imagesc(Xfv);
%% part e
ymat = zeros(640,640);
umat = zeros(640,640);
vmat = zeros(640,640);
for row=1:8:639
for col=1:8:639
xb=x(row:row+7,col:col+7,:);
r=xb(:,:,1);g=xb(:,:,2);b=xb(:,:,3);
y=0.299*r+0.587*g+0.114*b;
u=b-y;
v=r-y;
%% part b: apply the 2d-dct
n=8;
for i=1:n
for j=1:n
C(i,j)=cos((i-1)*(2*j-1)*pi/(2*n));
end
end
C=sqrt(2/n)*C;
C(1,:)=C(1,:)/sqrt(2);
y = y-128;
u = u-128;
v = v-128;
Yy=C*y*C';
Yu=C*u*C';
Yv=C*v*C';
%% parts c and d
% p=1
p=8;
Q=p*8./hilb(8);
Yqy=round(Yy./Q)
Yqu=round(Yu./Q)
Yqv=round(Yv./Q)
% dequantization step
Ydqy=Yqy.*Q;
Ydqu=Yqu.*Q;
Ydqv=Yqv.*Q;
Xdqy=C'*Ydqy*C; % inverse dct
Xdqu=C'*Ydqu*C; % inverse dct
Xdqv=C'*Ydqv*C; % inverse dct
Xey=Xdqy+128;
Xeu=Xdqu+128;
Xev=Xdqv+128;
Xfy=uint8(Xey);
Xfu=uint8(Xeu);
Xfv=uint8(Xev);
ymat(row:row+7,col:col+7)=Xfy;
umat(row:row+7,col:col+7)=Xfu;
vmat(row:row+7,col:col+7)=Xfv;
end
end
% rgb images
r=x(:,:,1);g=x(:,:,2);b=x(:,:,3);
y=0.299*r+0.587*g+0.114*b;
u=b-y;
v=r-y;
% figure(1)
% imagesc(y);
% figure(2)
% imagesc(u);
% figure(3)
% imagesc(v);
% figure(4)
% imagesc(ymat);
% figure(5)
% imagesc(umat);
% figure(6)
% imagesc(vmat);
% complete images
rgb=zeros(640,640,3);
rgb(:,:,1)=v+y;
rgb(:,:,2)=(y-0.299*r-0.114*b)/(0.587);
rgb(:,:,3)=u+y;
rgb=uint8(rgb);
figure(7)
imagesc(rgb);
rgbmat=zeros(640,640,3);
rgbmat(:,:,1)=vmat+ymat;
rgbmat(:,:,2)=(ymat-0.299*r-0.114*b)/(0.587);
rgbmat(:,:,3)=umat+ymat;
rgbmat=uint8(rgbmat);
figure(8)
imagesc(rgbmat);


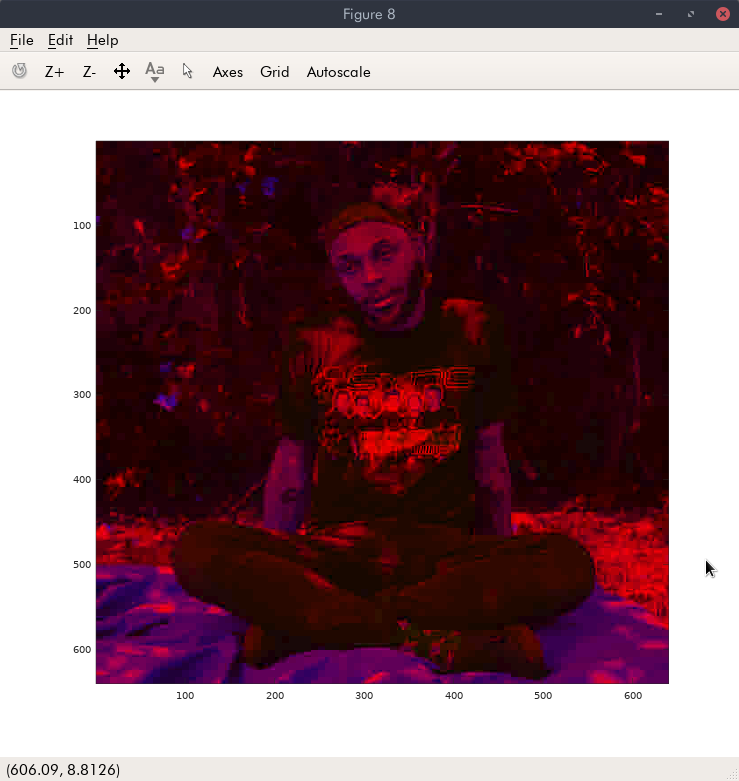
Displaying the YUV directly:
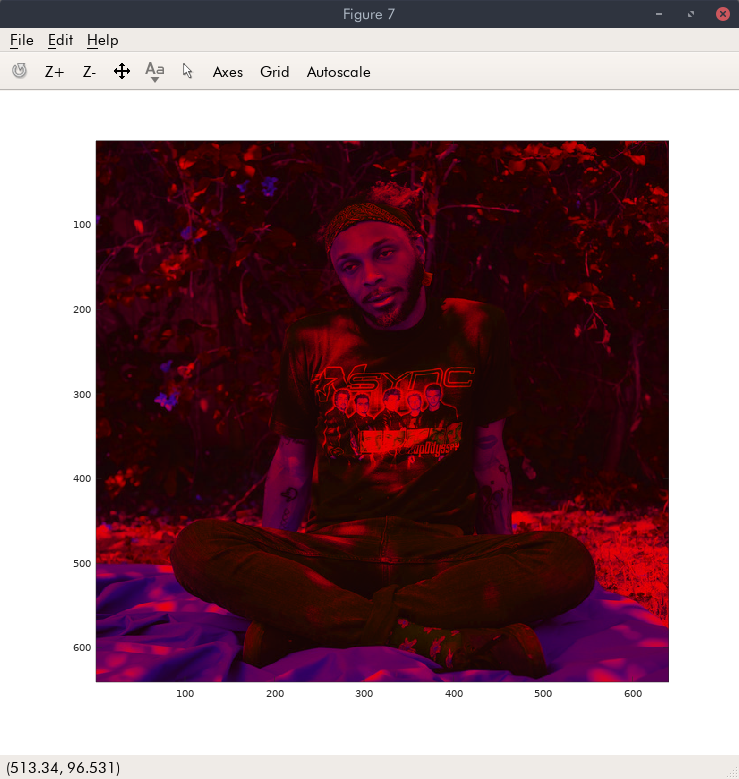
The YUV compressed using :
hack the world