Project 1: Kinematics of the Stewart Platform

Matthew Herman, Mark Schools, and John Wilson

Background

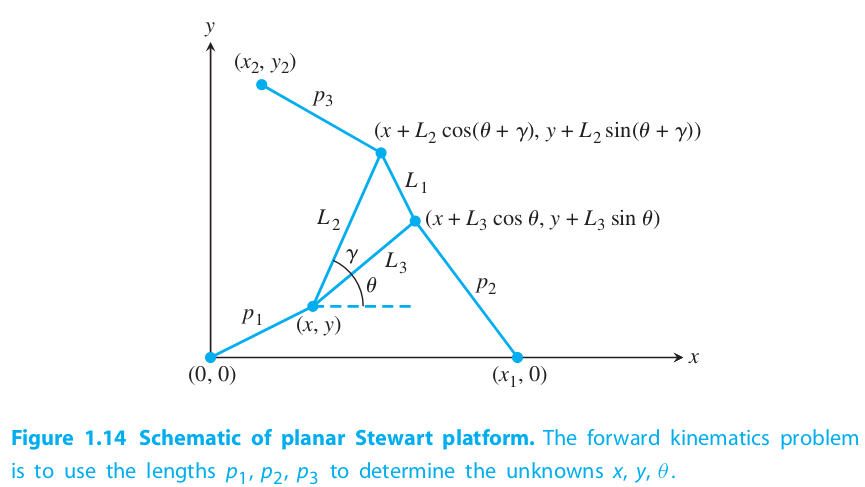
In this project, we simulated a simplified version of a Stewart platform. In our version, as opposed to six variable-length struts, we only account for three, which elevate and maneuver a triangular platform. The main goal of this project was to find the position of the platform, given the three strut lengths, by solving the forward kinematics problem. In this instance, this meant computing (x,y)(x,y) and .theta.theta for p1,p2,p3p_1, p_2, p_3.

To start, we were given formulas for p12,p22,p32p_1^2, p_2^2, p_3^2, derived using simple trigonometry: p12=x2+y2p_1^2 = x^2 + y^2,  p22=(x+A2)2+(y+B2)2\space p_2^2 = (x + A_2)^2 + (y + B_2)^2,  p32=(x+A3)2+(y+B3)2\space p_3^2 = (x + A_3)^2 + (y + B_3)^2. In these formulas, A2=L3cos⁡θ−x1A_2 = L_3 \cos \theta - x_1,  B2=L3sin⁡θ\space B_2 = L_3 \sin \theta,  A3=L2cos⁡(θ+γ)−x2=L2[cos⁡θcos⁡γ−sin⁡θsin⁡γ]−x2\space A_3 = L_2 \cos (\theta + \gamma) - x_2 = L_2 [ \cos \theta \cos \gamma - \sin \theta \sin \gamma ] - x_2, and  B3=L2sin⁡(θ+γ)−y2=L2[cos⁡θcos⁡γ+sin⁡θsin⁡γ]−y2\space B_3 = L_2 \sin (\theta + \gamma) - y_2 = L_2 [ \cos \theta \cos \gamma + \sin \theta \sin \gamma ] - y_2.

Multiplying out the equations for p22p_2^2 and p32p_3^2, substituting the first, then solving for xx and yy yields x=N1D=B3(p22−p12−A22−B22)−B2(p32−p12−A32−B32)2(A2B3−B2A3)x = \frac{N_1}{D} = \frac{B_3 (p_2^2 - p_1^2 - A_2^2 - B_2^2) - B_2(p_3^2 - p_1^2 - A_3^2 - B_3^2)}{2(A_2 B_3 - B_2 A_3)} and y=N2D=−A3(p22−p12−A22−B22)+A2(p32−p12−A32−B32)2(A2B3−B2A3)y = \frac{N_2}{D} = \frac{-A_3 (p_2^2 - p_1^2 - A_2^2 - B_2^2) + A_2(p_3^2 - p_1^2 - A_3^2 - B_3^2)}{2(A_2B_3 - B_2A_3)}, as long as D=2(A2B3−B2A3)≠0D = 2(A_2 B_3 - B_2 A_3) \neq 0.

Substituting these expressions for xx and yy into the equation for p12p_1^2 and multiplying by D2D^2 yields an expression f(θ)=N12+N22−p12D2=0f(\theta) = N_1^2 + N_2^2 - p_1^2D^2 = 0. Finding the roots of f(θ)f(\theta) we can easily determine the corresponding xx and yy values using the equations previously stated.

Part 1

Part 1 of this project called for simply translating the formulas listed above into MATLAB code:

12345678910111213141516function [out,n1,n2,n3] = f1(theta,x,y2,L,gamma,p)
  A2 = L(3) * cos(theta) - x(1);
  B2 = L(3) * sin(theta);
  A3 = L(2) * cos(theta + gamma) - x(2);
  B3 = L(2) * sin(theta + gamma) - y2;

  N1 = B3 .* (p(2).^2 - p(1).^2 - A2.^2 - B2.^2) - B2.* (p(3).^2 - p(1).^2 - A3.^2 - B3.^2);
  N2 = -A3.* (p(2).^2 - p(1).^2 - A2.^2 - B2.^2) + A2.* (p(3).^2 - p(1).^2 - A3.^2 - B3.^2);
  D = 2 * (A2.*B3-B2.*A3);

  out=N1.^2+N2.^2-p(1).^2*D.^2;

  n1 = [N1/D,N2/D];
  n2 = [n1(1) + L(3)*cos(theta), n1(2) + L(3)* sin(theta)];
  n3 = [n1(1) + L(2)*cos(theta+gamma), n1(2) + L(2)* sin(theta + gamma)];
end

To test this code, we set the parameters L1=2,L2−L3−2,γ=π/2,p1=p2=p3=5L_1 = 2, L_2 - L_3 - \sqrt{2}, \gamma = \pi / 2, p_1 = p_2 = p_3 = \sqrt{5}, then substituted θ=−π/4\theta = -\pi / 4 and ensured that f(θ)=0f(\theta) = 0:

12345678910111213141516171819L1 = 2;
L2 = sqrt(2);
L3 = L2;
L = [L1 L2 L3];

gamma = pi/2;

p1 = sqrt(5);
p2 = p1;
p3 = p1;
p= [p1 p2 p3];

x1 = 4;
y1 = 0;

x2 = 0;
y2 = 4;

x = [x1,x2];

Part 2

For Part 2, we plotted f(θ)f(\theta) on the interval [−π,π][-\pi, \pi], ensuring that there were roots at ±π/4\pm \pi / 4 as a check of our work:

123456789101112xint = -pi:0.1:pi;
out = @f1;
out1 = out(xint,x,y2,L,gamma,p);

figure(1)
plot(xint,out1)
hold on
grid
p2roots1 = secant_method(0,1,10,x,y2,L,p,gamma)
p2roots2 = secant_method(-1,0,10,x,y2,L,p,gamma)
plot([p2roots1 p2roots2],[0 0],'bo')
hold off

Running this code yielded the following:

12345678p2roots1 =

    0.7854


p2roots2 =

   -0.7808

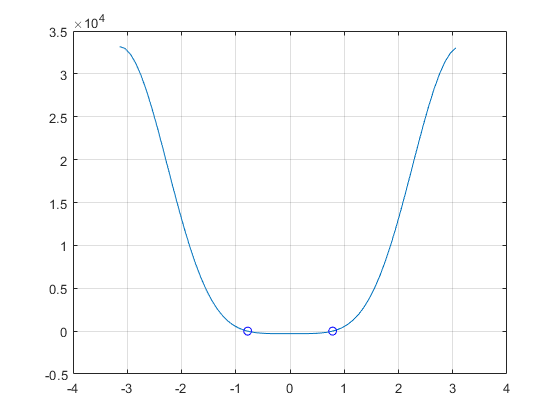
The roots returned by our code and displayed on the graph are equivalent to ±π/4\pm \pi / 4, so our results were sound.

Part 3

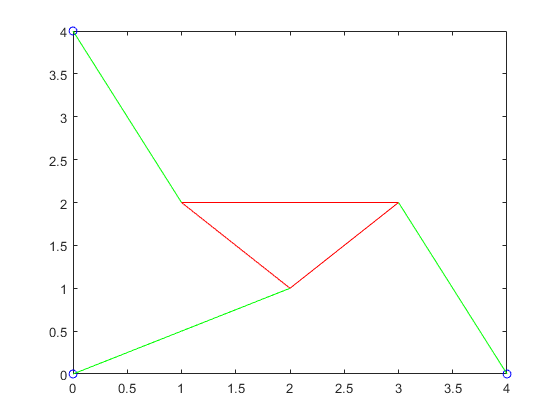
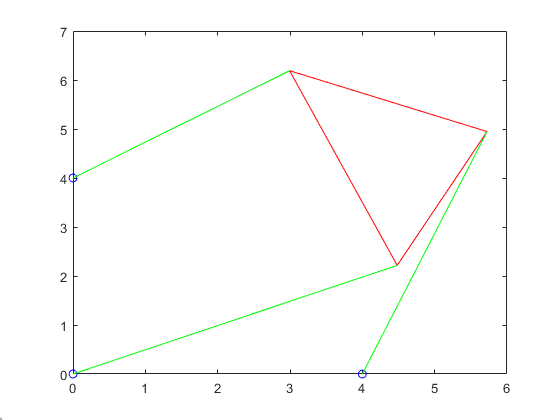
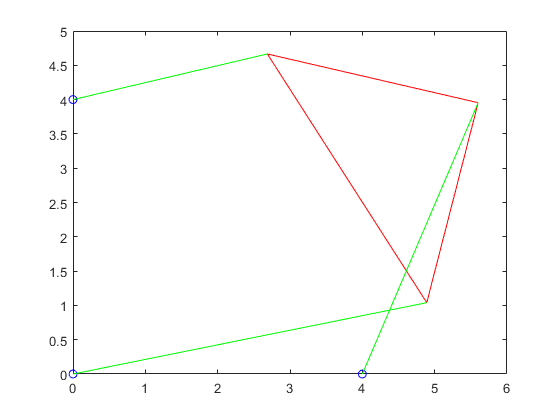
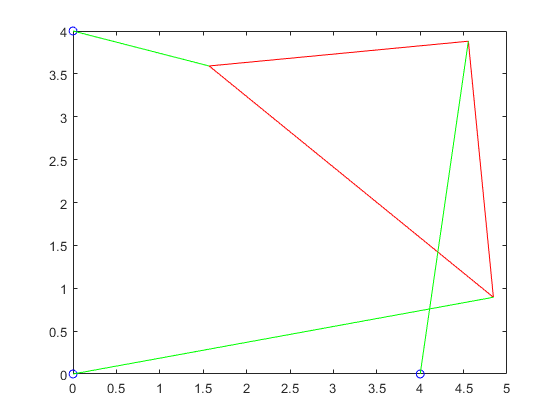
12p3struts1 = plotTriangle(p2roots1,x,y2,L,gamma,p,2)
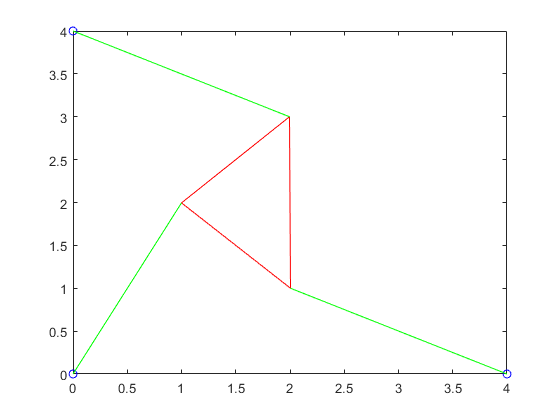
p3struts2 = plotTriangle(p2roots2,x,y2,L,gamma,p,3)

12345678910p3struts1 =

    2.2361    2.2361    2.2361
    2.2361    2.2361    2.2361


p3struts2 =

    2.2320    2.2320    2.2320
    2.2361    2.2361    2.2361

Part 4

1234567891011121314151617181920212223242526272829303132function out=secant_method(theta0,theta1,i,x,y2,L,p,gamma)
y = @f1;
for(j=1:i)
theta2 = theta1 - ((y(theta1,x,y2,L,gamma,p) * (theta1 - theta0)) / ...
(y(theta1,x,y2,L,gamma,p) - y(theta0,x,y2,L,gamma,p)));
theta0 = theta1;
theta1 = theta2;
end out=theta1;
end

x = [5 0];
y2 = 6;
L = [3 (3*sqrt(2)) 3];
gamma = pi/4;
p = [5.0 5.0 3.0];

figure(4)
hold on
grid
out4 = out(xint,x,y2,L,gamma,p);
plot(xint,out4)
p5roots1 = secant_method(-.8,-.6,5,x,y2,L,p,gamma)
p5roots2 = secant_method(-.4,-.2,5,x,y2,L,p,gamma)
p5roots3 = secant_method(2,2.6,5,x,y2,L,p,gamma)
p5roots4 = secant_method(1,1.2,5,x,y2,L,p,gamma)
plot([p5roots1 p5roots2 p5roots3 p5roots4],[0 0 0 0],'bo')
hold off

p5struts1 = plotTriangle(p5roots1,x,y2,L,gamma,p,5)
p5struts2 = plotTriangle(p5roots2,x,y2,L,gamma,p,6)
p5struts3 = plotTriangle(p5roots3,x,y2,L,gamma,p,7)
p5struts4 = plotTriangle(p5roots4,x,y2,L,gamma,p,8)

123456789101112131415161718192021222324252627282930313233343536373839404142p5roots1 =

   -0.7209


p5roots2 =

   -0.3310


p5roots3 =

    2.1159


p5roots4 =

    1.1437


p5struts1 =

    5.0000    5.0000    3.0000
    5.0000    5.0000    3.0000


p5struts2 =

    5.0000    5.0000    3.0000
    5.0000    5.0000    3.0000


p5struts3 =

    5.0000    5.0000    3.0000
    5.0000    5.0000    3.0000


p5struts4 =

    5.0000    5.0000    3.0000
    5.0000    5.0000    3.0000

Part 5

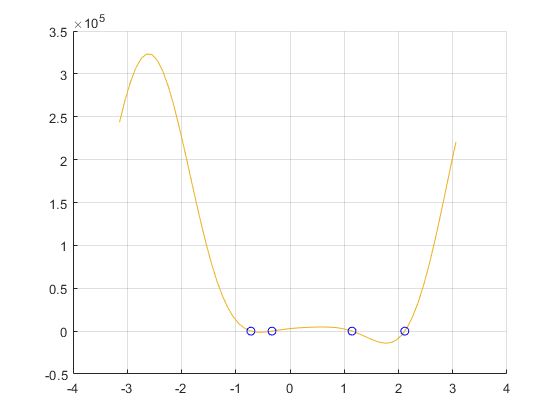
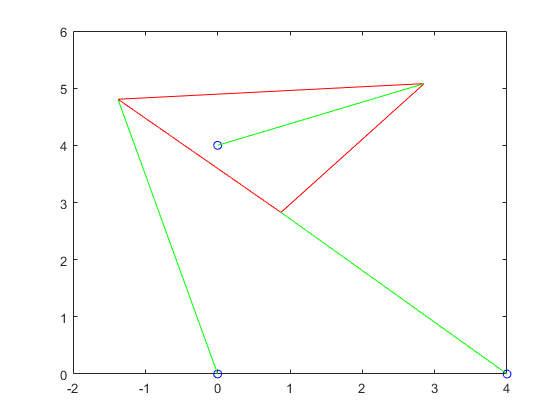
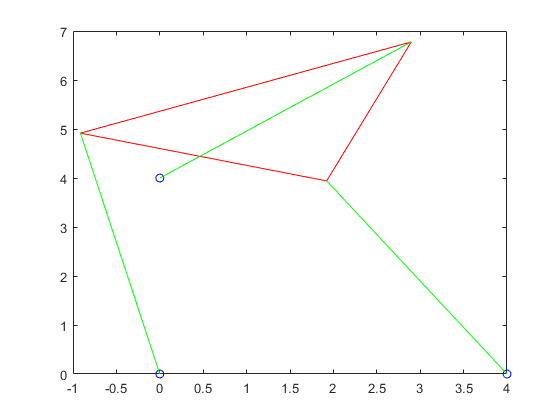
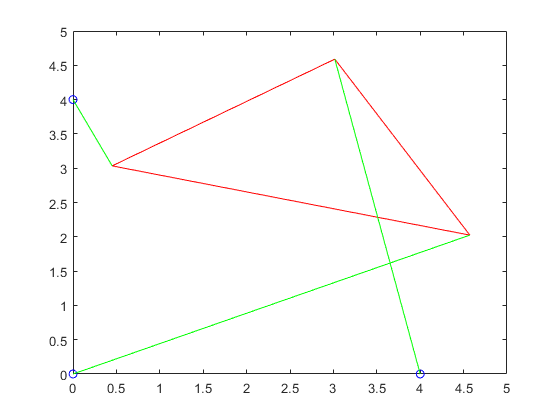
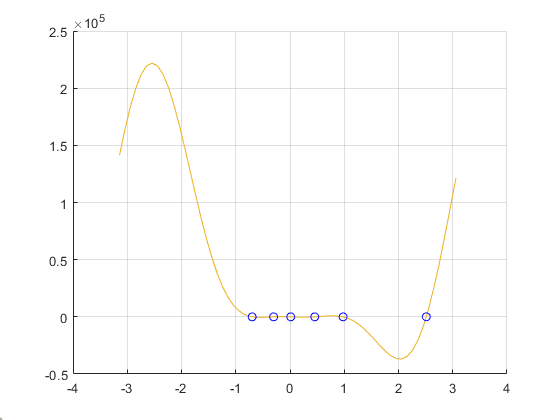
For this one, the functions are all the same as the previous ones, the only differences being that the structs that were hard coded in are changed, making 6 roots in stead of the 4 we saw in part 4.

123456789101112131415161718192021p(2) = 6.99;
figure(9)
hold on
grid
out5 = out(xint,x,y2,L,gamma,p);
plot(xint,out5)
p5roots1 = secant_method(-.8,-.6,5,x,y2,L,p,gamma)
p5roots2 = secant_method(-.4,-.2,5,x,y2,L,p,gamma)
p5roots3 = secant_method(-.2,.2,5,x,y2,L,p,gamma)
p5roots4 = secant_method(.3,.5,5,x,y2,L,p,gamma)
p5roots5 = secant_method(2,2.6,5,x,y2,L,p,gamma)
p5roots6 = secant_method(1,1.2,5,x,y2,L,p,gamma)
plot([p5roots1 p5roots2 p5roots3 p5roots4 p5roots5 p5roots6],[0 0 0 0 0 0],'bo')
hold off

p5struts1 = plotTriangle(p5roots1,x,y2,L,gamma,p,10)
p5struts2 = plotTriangle(p5roots2,x,y2,L,gamma,p,11)
p5struts3 = plotTriangle(p5roots3,x,y2,L,gamma,p,12)
p5struts4 = plotTriangle(p5roots4,x,y2,L,gamma,p,13)
p5struts5 = plotTriangle(p5roots5,x,y2,L,gamma,p,14)
p5struts6 = plotTriangle(p5roots6,x,y2,L,gamma,p,15)

12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364p5roots1 =

   -0.6970


p5roots2 =

   -0.3035


p5roots3 =

    0.0139


p5roots4 =

    0.4560


p5roots5 =

    2.5128


p5roots6 =

    0.9780


p5struts1 =

    5.0000    6.9900    3.0001
    5.0000    6.9900    3.0000


p5struts2 =

    5.0000    6.9900    3.0000
    5.0000    6.9900    3.0000


p5struts3 =

    5.0000    6.9900    3.0000
    5.0000    6.9900    3.0000


p5struts4 =

    5.0000    6.9900    3.0000
    5.0000    6.9900    3.0000


p5struts5 =

    5.0000    6.9900    3.0000
    5.0000    6.9900    3.0000


p5struts6 =

    5.0000    6.9900    3.0000
    5.0000    6.9900    3.0000

Part 6

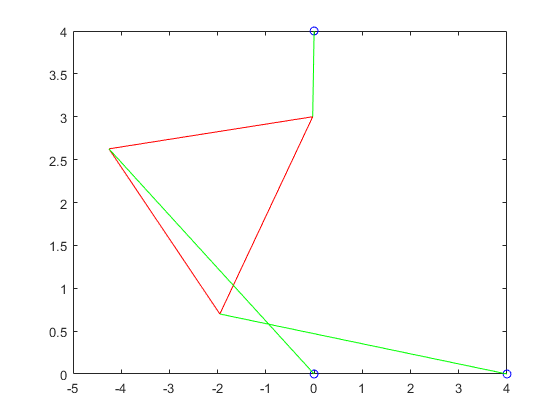
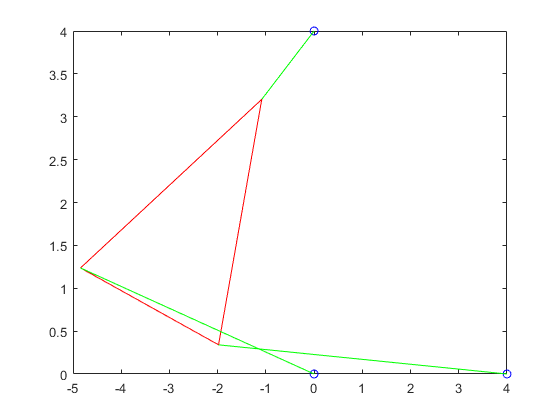
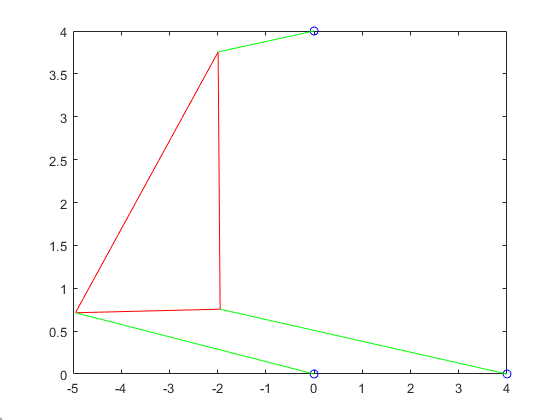
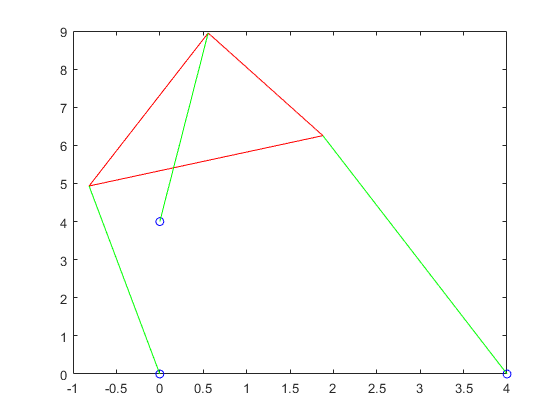
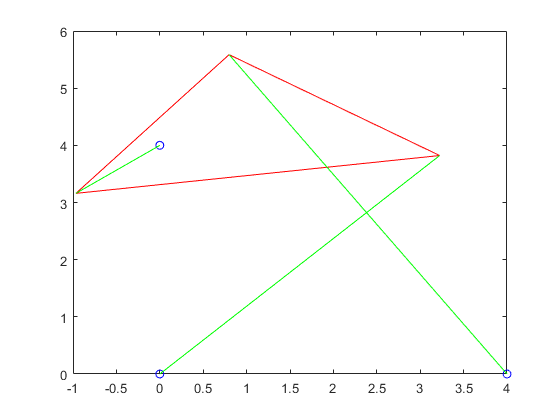
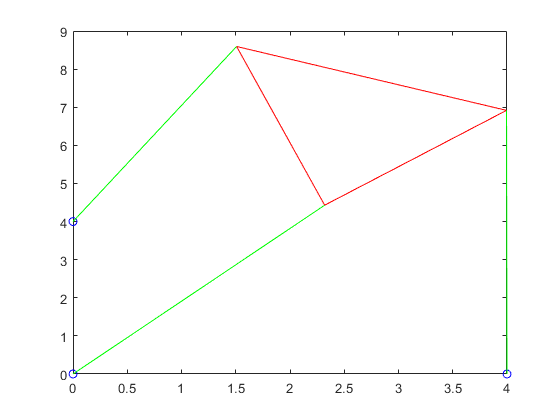
For this part, we had had to rewrite the function from part 1 to instead graph the possible p2p_2s instead of the possible values for θ\theta same goes all the other fuctions.

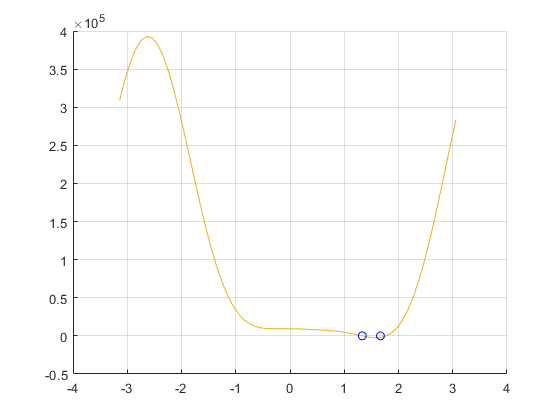
123456789101112p(2) = 4;
figure(16)
hold on
grid
out6 = out(xint,x,y2,L,gamma,p);
plot(xint,out6)
p6roots1 = secanat_method(1,1,5,5,x,y2,L,p,gamma)
p6roots2 = secanat_method(1,5,2,5,x,y2,L,p,gamma)
plot([p6roots1 p6roots2], [0 0], 'bo')
hold off
p6struts1 = plotTriangle(p6roots1,x,y2,L,gamma,p,17)
p6struts2 = plotTriangle(p6roots2,x,y2,L,gamma,p,18)

References

Sauer, T. (2018). Numerical Analysis (3rd ed.) Boston: Pearson.