Google Page Rank eigen vectors
Group members: James Aviles
Contents
Summary
Googles page rank is defined by using the eigenvalues of a matrix which is defined by the connections a website has TO and FROM itself (also known as a node network.
By defining the probabilty of being on a given node as the inverse of the sum of its connections and then multiplying this matrix with the original matrix we achieve the google page rank matrix (which is a matrix of the proportions of time spent at a given node.)
We then compute and pull the eigenvector corresponding to eigen value = 1 from the set of eigenvectors retrieved using matlabs eig() function
Example
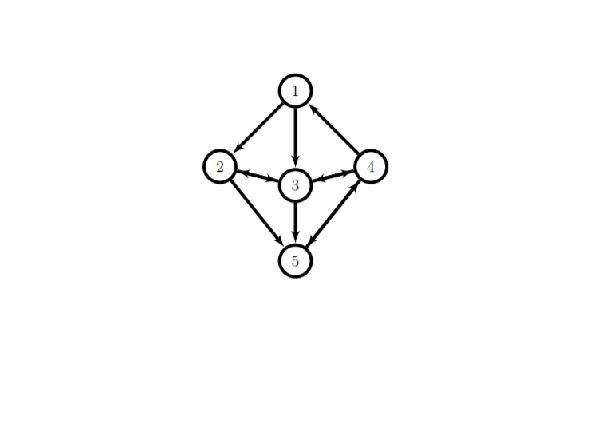
imshow('1.png') example =[0 0 0 1 0 % here we define the network according to connections 1 0 1 0 0; % F R O M 1 1 0 1 0; % T 0 0 1 0 1; % O 0 1 1 1 0] %
example =
0 0 0 1 0
1 0 1 0 0
1 1 0 1 0
0 0 1 0 1
0 1 1 1 0
D = diag(sum(example,1))% Define matrix D as the sum of a nodes connections G=example*inv(D) % Define Google rank matrix as the the node matrix % multiplied by the inverse of the Sum of nodes % matrix (which defines the probability) [eigvec,eigval]=eig(G) % extract the eigen vectors and values from G v=eigvec(:,1) % Take the eigen vector corresponding to eigen value of 1 v=v/sum(v) % Normalize that vector to represent probabilities
D =
2 0 0 0 0
0 2 0 0 0
0 0 3 0 0
0 0 0 3 0
0 0 0 0 1
G =
0 0 0 0.3333 0
0.5000 0 0.3333 0 0
0.5000 0.5000 0 0.3333 0
0 0 0.3333 0 1.0000
0 0.5000 0.3333 0.3333 0
eigvec =
Columns 1 through 4
0.2175 + 0.0000i 0.0353 - 0.4315i 0.0353 + 0.4315i -0.3122 + 0.0000i
0.2610 + 0.0000i -0.4689 + 0.1415i -0.4689 - 0.1415i 0.3660 + 0.0000i
0.4567 + 0.0000i -0.3074 + 0.0000i -0.3074 - 0.0000i -0.3484 + 0.0000i
0.6525 + 0.0000i 0.6149 + 0.0000i 0.6149 + 0.0000i 0.6968 + 0.0000i
0.5002 + 0.0000i 0.1262 + 0.2901i 0.1262 - 0.2901i -0.4021 + 0.0000i
Column 5
0.2209 + 0.0000i
0.4417 + 0.0000i
-0.7730 + 0.0000i
-0.2209 + 0.0000i
0.3313 + 0.0000i
eigval =
Columns 1 through 4
1.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0386 + 0.4718i 0.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i 0.0386 - 0.4718i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.7438 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i
Column 5
0.0000 + 0.0000i
0.0000 + 0.0000i
0.0000 + 0.0000i
0.0000 + 0.0000i
-0.3333 + 0.0000i
v =
0.2175
0.2610
0.4567
0.6525
0.5002
v =
0.1042
0.1250
0.2188
0.3125
0.2396
In the example case, the fourth node is ranked the highest
Problem 1
We have summarized the above code into the function 'prank'
We must now solve for the google page rank of the following matrix
imshow('2.png')
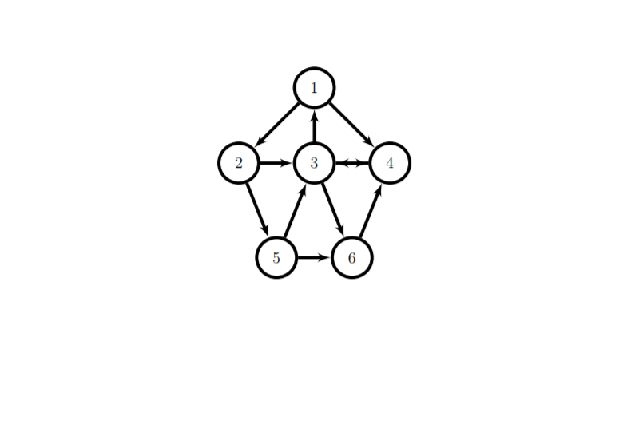
problem1=[0 0 1 0 0 0 % define the matrix 1 0 0 0 0 0; 0 1 0 1 1 0; 1 0 1 0 0 1; 0 1 0 0 0 0; 0 0 1 0 1 0] prank(problem1) % Solve for the google page rank
problem1 =
0 0 1 0 0 0
1 0 0 0 0 0
0 1 0 1 1 0
1 0 1 0 0 1
0 1 0 0 0 0
0 0 1 0 1 0
v =
0.1176
0.0588
0.3529
0.3088
0.0294
0.1324
ans =
0.1176
0.0588
0.3529
0.3088
0.0294
0.1324
For problem 1, the third node is ranked the highest
Problem 2
Do the same for this next network
imshow('3.png')
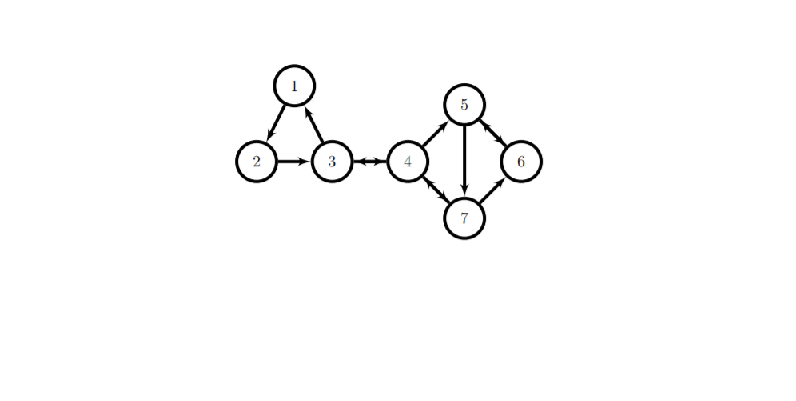
problem2=[0 0 1 0 0 0 0
1 0 0 0 0 0 0;
0 1 0 1 0 0 0;
0 0 1 0 0 0 1;
0 0 0 1 0 1 0;
0 0 0 0 1 0 1;
0 0 0 1 1 0 0]
prank(problem2)
problem2 =
0 0 1 0 0 0 0
1 0 0 0 0 0 0
0 1 0 1 0 0 0
0 0 1 0 0 0 1
0 0 0 1 0 1 0
0 0 0 0 1 0 1
0 0 0 1 1 0 0
v =
0.0455
0.0455
0.0909
0.1364
0.2727
0.2273
0.1818
ans =
0.0455
0.0455
0.0909
0.1364
0.2727
0.2273
0.1818
For problem 2, the fifth node is ranked highest
the following network is of my own creation
imshow('4.png')
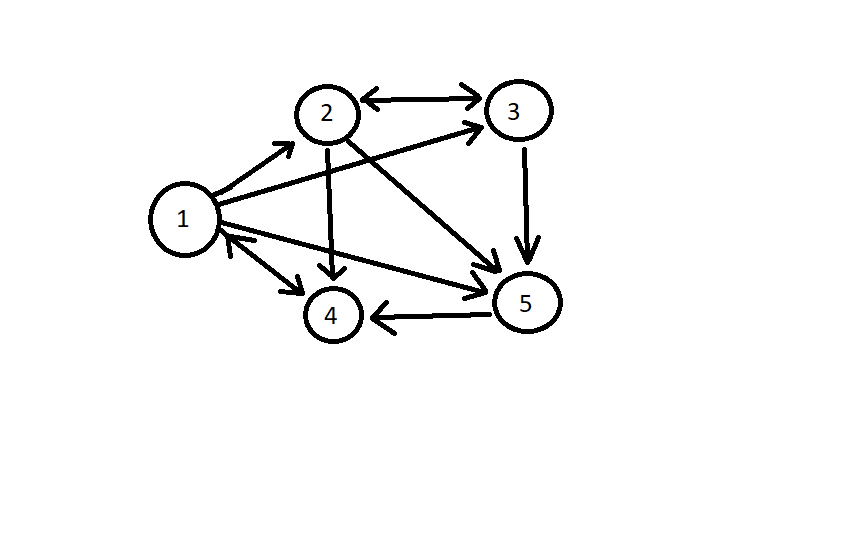
problem3=[0 0 0 1 0
1 0 1 0 0;
1 1 0 0 0;
1 1 0 0 1;
1 0 1 0 0]
prank(problem3)
problem3 =
0 0 0 1 0
1 0 1 0 0
1 1 0 0 0
1 1 0 0 1
1 0 1 0 0
v =
0.2857
0.1429
0.1429
0.2857
0.1429
ans =
0.2857
0.1429
0.1429
0.2857
0.1429
I had initially planned on checking the case for the page rank of node 1 when it was connected to all nodes but no nodes were connected to it. however this was throwing an error because node 1 would have a page rank value of 0
upon connecting node 5 to 4, and node 4 to 1, every node then obtained a value which allowed the program to continue.
interestingly node 4 and 1 have the same page rank, because node 4 needs only to connect to node 1 in order to piggy back off of its connections to increase its page rank.