Celestial Mechanics
Group Member: James Aviles, Michael Belete, Faysal Shaikh
Assignment following 'Clestial Mechanics' on Timothy Sauer's Website
Initial Code for 'Orbit.m' Provided here
Contents
Computer Problem 9
In this section we adapt the provided orbit.m file to solve the two body problem with initial conditions:
mass 1 = 0.03, mass 2 = 0.3
x1,y1 (position) = (2,2)
x1',y1' (velocity) = (0.2,-0.2)
x2, y2 (2nd mass position) = (0,0)
x2',y2' (2nd mass velocity) = (-0.02,0.02)
Click Here to view orbit for 2 body function
% initial condition list entered in following order: % x1 pos, x1 vel, y1 pos, y1 vel, x2 pos, x2 vel, y2 pos, y2 vel ic1 = [2 0.2 2 -0.2 0 -0.02 0 0.02]; % initial conditions ma = [0.03 0.3]; % masses inter1 = [0 500]; %interval on which it is plotted n1 = 50000; % for step size h=0.01 n2 = 500000; % for step size h=0.001 % orbit2body(inter1,ic1,n1,10,ma); will create first video
Computer Problem 10
Using the code in Computer Problem 9 examine these initial conditions:
initial conditions: [0 0.1 1 -0.1 -2 -0.01 -1 0.01]
interval [0,500]
% masses: % (a) m1 = 0.03, m2 = 0.3 % (b) m1 = 0.05, m2 = 0.5 % (c) m1 = 0.08, m2 = 0.8 % % using step size h = 0.01 and 0.001 for each set of masses % ic1 = [0 0.1 1 -0.1 -2 -0.01 -1 0.01]; %initial conditions ma = [0.03 0.3]; % part a masses mb = [0.05 0.5]; % part b masses mc = [0.08 0.8]; % part c masses inter1 = [0 500]; % interval n1 = 50000; % value for h = 0.01 n2 = 500000; % value for h = 0.001 % orbit2body(inter1,ic1,n1,10,ma); first video (masses a, h=0.01) % orbit2body(inter1,ic1,n2,10,ma); second video (masses a, h=0.001) % orbit2body(inter1,ic1,n1,10,mb); third video (masses b, h=0.01) % orbit2body(inter1,ic1,n2,10,mb); fourth video (masses b, h=0.001) % orbit2body(inter1,ic1,n1,10,mc); fifth video (masses c, h=0.01) % orbit2body(inter1,ic1,n2,10,mc); sixth video (masses c, h=0.001)
ma = [0.03 0.3], h = 0.01
ma = [0.03 0.3], h = 0.001
mb = [0.05 0.5], h = 0.01
mb = [0.05 0.5], h = 0.001
mc = [0.08 0.8], h = 0.01
mc = [0.08 0.8], h = 0.001
QUESTION: Do you believe the Trapezoid Method is giving reliable estimates of the trajectories? Are there particular points in the trajectories that cause problems?
ANSWER: The trapezoid method is giving a reliable estimate of the trajectories when looking at the smaller step size used. When looking at the larger step size the trapezoid method appears to be very unreliable.
Computer Problem 11
Repeat Computer Problem 10 with the following Conditions:
ic1 = [0 0.2 1 -0.2 -2 -0.2 -1 0.2]; %initial conditions ma = [2 2]; % part a masses mb = [1 1]; % part b masses mc = [0.5 0.5]; % part c masses inter1 = [0 500]; %interval n1 = 50000; % value for h = 0.01 % orbit2body(inter1,ic1,n1,10,ma); first video (masses a, h=0.01) % orbit2body(inter1,ic1,n1,10,mb); second video (masses b, h=0.01) % orbit2body(inter1,ic1,n1,10,mc); third video (masses c, h=0.01)
ma = [2,2] h = 0.01
mb = [1,1] , h = 0.01
mc = [0.5 0.5], h = 0.01
QUESTION: Do you believe the Trapezoid Method is giving reliable estimates of the trajectories? Are there particular points in the trajectories that cause problems?
ANSWER: For the smaller masses used in parts c and b the Trapezoid method is giving pretty reliable estimates of the trajectories but even in our small interval you can see how unreliable the trapezoid method is for the trajector with a larger mass.
Computer Problem 12
Adapt orbit to solve the 3 body problem
Click here to see Code for 3 bodies
Use the following innitial conditions in Computer Problem 12
ic1 = [2 0.2 2 -0.2 0 0 0 0 -2 -0.2 -2 0.2]; %initial conditions part a ic2 = [2 0.20001 2 -0.2 0 0 0 0 -2 -0.2 -2 0.2]; %slight change in x1 vel ma = [0.03 0.3 0.03]; %masses inter1 = [0 500]; %interval n1 = 50000; %h=0.01 % orbit2body(inter1,ic1,n1,10,ma); first video (x1 vel = 0.2) % orbit2body(inter1,ic2,n1,10,ma); second video (x1 vel = 0.20001)
with regular initial conditions
with x1' = 0.20001 a slight change in the initial velocity of one body made the orbits chaotic
Computer Problem 13
Add a third body to the two bodies from Computer Problem 10 with the following initial conditions
ic1 = [0 0.1 1 -0.1 -2 -0.01 -1 0.01 4 -0.2 3 0]; %initial conditions (adding third body to #10) ma = [0.03 0.3 0.0001]; % part a masses mb = [0.05 0.5 0.0001]; % part b masses mc = [0.08 0.8 0.0001]; % part c masses inter1 = [0 500]; %interval n1 = 50000; % h=0.01 n2 = 500000; % h=0.001 % third body is black with green tail. % orbit2body(inter1,ic1,n1,10,ma); first video (masses a, h=0.01) % orbit2body(inter1,ic1,n2,10,ma); second video (masses a, h=0.001) % orbit2body(inter1,ic1,n1,10,mb); third video (masses b, h=0.01) % orbit2body(inter1,ic1,n2,10,mb); fourth video (masses b, h=0.001) % orbit2body(inter1,ic1,n1,10,mc); fifth video (masses c, h=0.01) % orbit2body(inter1,ic1,n2,10,mc); sixth video (masses c, h=0.001)
ma = [0.03 0.3 0.0001], h = 0.01
ma = [0.03 0.3 0.0001], h = 0.001
mb = [0.05 0.5 0.0001], h = 0.01
mb = [0.05 0.5 0.0001], h = 0.001
mc = [0.08 0.8 0.0001], h = 0.01
mc = [0.08 0.8 0.0001], h = 0.001
QUESTION: Does the original trajectory from Computer Problem 10 change appreciably?
ANSWER: As the step size and mass increase the trejctory of the original two bodies changes more drastically. The Orbit of the third bodie is very erratic and the third body often flies far away from the other two bodies.
Computer Problem 14
Investigate the three-body problem of a sun and two planets with the following initial conditions
ic1 = [0 0.6 2 0.05 0 -0.03 0 0 4 0 3 -0.5]; % initial conditions ma = [0.05 1 0.005]; % masses inter1 = [0 500]; % interval n1 = 50000; % h=0.01 n2 = 500000; % h=0.001 % sun is yellow with black tail (orbit), planets are red with blue tail (orbit). % orbit3body(inter1,ic1,n1,10,ma); first video (h=0.01) % orbit3body(inter1,ic1,n2,10,ma); second video (h=0.001)
h = 0.01
h = 0.001
QUESTION: Do you believe the Trapezoid Method is giving reliable estimates of the trajectories? Are there particular points in the trajectories that cause problems?
ANSWER: The trapezoid method appears to be giving unreliable estimates of the trajectories. The particular points of the trajectories that are causing the most problems are those further away from the sun that the outer planet is orbiting. Increasing the step size does not greatly alleviate these problems.
Computer Problem 15
Investigate the three-body problem of a sun, planet, and comet with the following initial conditions
ic1 = [0 0.6 2 0 0 -0.03 0 0 4 -0.2 3 0]; % initial conditions ma = [0.05 1 0.00001]; % masses inter1 = [0 500]; % interval n1 = 50000; % h=0.01 n2 = 500000; % h=0.001 % comet is green with black tail (orbit), sun is yellow with % black tail (orbit), planet is red with blue tail (orbit) % orbit3body(inter1,ic1,n1,10,ma); first video (h=0.01) % orbit3body(inter1,ic1,n2,10,ma); second video (h=0.001)
h = 0.01
h = 0.001
QUESTION: Do you believe the Trapezoid Method is giving reliable estimates of the trajectories? Are there particular points in the trajectories that cause problems?
ANSWER: The trapezoid method appears to be giving unreliable estimates of the trajectories. The particular points of the trajectories that are causing the most problems are the points along the trajectory of the comet when it is further away from the sun. Increasing the step size does not alleviate this problem.
Computer Problem 16
Observe the orbit of three bodies of equal mass chasing eachother along a single figure-eight and investigate the effect of small changes in the initial conditions by changing the x-velocity of the third body by 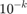 for
for 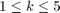
ic1 = [-0.970 -0.466 0.243 -0.433 0.970 -0.466 -0.243 -0.433 0 0.9320 0 0.8660]; %initial conditions icb1 = [-0.970 -0.466 0.243 -0.433 0.970 -0.466 -0.243 -0.433 0 0.9320+0.00001 0 0.8660]; %k=5 changing x3' by 10^(-k)) icb2 = [-0.970 -0.466 0.243 -0.433 0.970 -0.466 -0.243 -0.433 0 0.9320+0.0001 0 0.8660]; %k=4 icb3 = [-0.970 -0.466 0.243 -0.433 0.970 -0.466 -0.243 -0.433 0 0.9320+0.001 0 0.8660]; %k=3 icb4 = [-0.970 -0.466 0.243 -0.433 0.970 -0.466 -0.243 -0.433 0 0.9320+0.01 0 0.8660]; %k=2 icb5 = [-0.970 -0.466 0.243 -0.433 0.970 -0.466 -0.243 -0.433 0 0.9320+0.1 0 0.8660]; %k=1 ma = [1 1 1]; %masses inter1 = [0 500]; %interval n1 = 50000; %h=0.01 % orbit3body(inter1,ic1,n1,10,ma); first video % orbit3body(inter1,icb1,n1,10,ma); second video (k=5) % orbit3body(inter1,icb2,n1,10,ma); third video (k=4) % orbit3body(inter1,icb3,n1,10,ma); fourth video (k=3) % orbit3body(inter1,icb4,n1,10,ma); fifth video (k=2) % orbit3body(inter1,icb5,n1,10,ma); sixth video (k=1)
no changes
k=5
k=4
k=3
k=2
k=1