Math 447 Project 2

GPS, Conditioning, and Nonlinear Least Squares

Reference: T. Sauer, 2012, Numerical Analysis, p.238-241(Reality Check 4)

Step 1

Matlab code (Click here)

Results (Click here)

Step 2

Matlab code (Click here)

Results (Click here)

Step 4 (Four unbunched satellites)

Set up new satellite locations using spherical coordinates, and find the maximum error magnification factor for all small \(\Delta t_i=10^{-8}\).

1) Location of four satellites and transmission time

2) The Maximum Error Magnification Factor

Define the dimensionless error magnification factor as follow, using the change in position caused by \(\Delta t_i=10^{-8}\).

3) Matlab code (Click here)

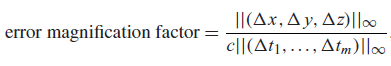
Followings are changed from Step1 code.

4) Results (Click here)

The maximum error magnification factor for all small \(\Delta t_i\) (condition number)

= 5.475302028519095.

Step 5 (Four bunched satellites)

Repeat Step 4 with a more tightly grouped set of satellites.

1) Location of four satellites and transmission time

From Step4, choose all \(\phi_i\) and \(\theta_i\) within 5 percent of one another.

2) Matlab code (Click here)

Only spherical coordinates of satellite positions were changed from Step4 code.

3) Results (Click here)

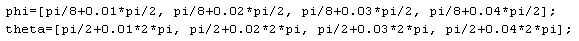
The maximum error magnification factor for all small \(\Delta t_i\) (condition number)

= 1.083912067236088e+05.

These tightly bunched satellites show larger condition number than the loosely bunched satellites in Step 4.

That is, tightly bunched satellites are less accurate than unbunched satellites.

Step 6 (Seven unbunched satellites)

Decide whether the GPS error and condition number can be reduced by adding satellites.

1) Location of four satellites and transmission time

Return to Step 4, and add three more satellites. Now assume that we know locations of seven satellites.

2) Matlab code (Click here)

Followings are changed from Step4 code. i) Seven satellite positions

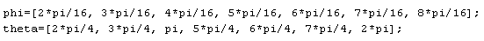
ii) Random 14 variations of the \(\Delta t_ią10^-8, i=1,..,7\) though possible combination is \(2^7\).

iii) Used Gauss-Newton iteration to solve the least squares system of seven equations in four variables (x, y, z, d).

3) Results (Click here)

The maximum error magnification factor for small \(\Delta t_i\) (condition number)

- The bunched satellites are less accurate than unbunched satellites.

- Adding more satellites does not provide more accurate position.