Optimal
Computing Budget Allocation (OCBA)
for
Efficient Simulation-based Decision Making Under Uncertainty
-- Simulation Optimization
by Professor
Chun-Hung Chen
This is Dr. Chen's current major research area. We have a state-of-the-art approach to intelligently allocate computing budget for efficient simulation optimization.
Simulation is a popular tool for designing large, complex, stochastic systems, since closed-form analytical solutions generally do not exist for such problems. While the advance of new technology has dramatically increased computational power, efficiency is still a big concern when using simulation for large system design, in which case many alternative designs must be simulated. To make the matter worse, multiple simulation runs must be performed for each design in order to catch stochastic behaviors in systems. How to dramatically reduce total computation time is the key issue in this topic.
A key component of our methodologies is our new control-theoretic simulation technique called Optimal Computing Budget Allocation (OCBA). The OCBA approach can intelligently determine the most efficient simulation replication numbers or simulation lengths for all simulated alternatives. The goal is to obtain the highest simulation decision quality using a fixed computing budget, or to attain a desired simulation decision quality using a minimum computing budget. Numerical testing shows that our approach can obtain the same simulation quality with only one-tenth the simulation effort.
OCBA is also ideal for stochastic simulation optimization. A primary reason that simulation optimization is difficult is the stochastic nature of evaluating the objective function, which means that there is a basic tradeoff between devoting computational effort on searching the space for new candidate solutions (exploration) versus getting more accurate estimates of the objective function at currently promising solutions (exploitation). In other words, how much of a simulation budget should be allocated to additional replications at already visited points and how much to replications at newly generated search points is a major consideration in terms of computational efficiency. In procedure, OCBA sequentially determines which design alternatives need more simulation and how many additional replications are needed.
Intuitively, to ensure that the best alternative is correctly selected, a larger portion of the computing budget should be allocated to those alternatives that are critical in the process of identifying the best alternative. In other words, a larger number of simulations must be conducted with those critical alternatives in order to reduce these critical estimators' variances. Overall simulation efficiency is improved as less computational effort is spent on simulating non-critical alternatives and more is spent on critical alternatives. The ideas are explained using the following simple example. Suppose we are performing simulations for 5 alternatives in order to determine an alternative with minimum mean delay. First of all, we conduct some preliminary simulation for all 5 alternatives. Figure 1-(a) gives an example of their 99% confidence intervals obtained from the preliminary simulation. Note that the uncertainty of estimation is due to the system's stochastic features and the use of Monte Carlo simulation.
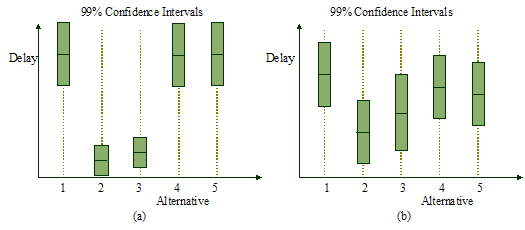
Figure
1. 99% confidence intervals
for five alternatives after some preliminary simulation in a (a) trivial case,
and (b) more common case.
As seen in Figure 1-(a), while there is uncertainty in the estimation of the performance for each alternative, it is obvious that alternatives 2 and 3 are much better than the other alternatives, if we intend to find an alternative with minimum mean delay. And so only alternatives 2 and 3 need to be further simulated to reduce estimation uncertainty in order to correctly identify the best alternative. By stopping simulations for alternatives 1, 4, and 5 earlier, we can save a lot of computation cost.
However, what actually happens in most cases is not as trivial as that shown in Figure 1-(a). It is more common to see cases like another example shown in Figure 1-(b), where some alternatives seem better, but are not clearly better than the others. It is not straightforward in such cases to determine which alternatives can be removed from the simulation experiment, and when they should be stopped. OCBA provides a systematic approach to address this problem and allocate simulation runs to alternatives in a way that the simulation efficiency is maximized.
To learn more about OCBA, the following two papers is a good starting point:
Theoretical
Foundation and Derivation of OCBA
Chen, C. H., J. Lin, E. Yücesan, and S. E. Chick, "Simulation Budget Allocation for Further Enhancing the Efficiency of Ordinal Optimization," Journal of Discrete Event Dynamic Systems: Theory and Applications, Vol. 10, pp. 251-270, July 2000. PDF
Introduction
of OCBA Ideas
Chen, C. H., and
Here are some more representative publications about the OCBA techniques.
Some Earlier Development of OCBA
Chen, C. H. "A Lower Bound for the Correct Subset-Selection Probability and Its Application to Discrete Event System Simulations," IEEE Transactions on Automatic Control, Vol. 41, No. 8, pp. 1227-1231, August 1996.
Chen, H. C., C. H. Chen, L. Dai, and
Chen, H. C., C. H. Chen, and E. Yücesan, "Computing Efforts Allocation for Ordinal Optimization and Discrete Event Simulation," IEEE Transactions on Automatic Control, Vol. 45, No. 5, pp. 960-964, May 2000.
OCBA for Selecting An Optimal Subset
of Top Designs (say top 5)
Chen, C. H., D. He, M. Fu, and L. H. Lee, "Efficient Simulation Budget Allocation for Selecting an Optimal Subset," to appear in Informs Journal on Computing, 2008.
OCBA for Selecting the Best
Alternative when Samples Are Correlated
Fu, M. C., J. Q. Hu, C. H. Chen, and X. Xiong, "Simulation Allocation for Determining the Best Design in the Presence of Correlated Sampling," Informs Journal on Computing, Vol. 19, No. 1, pp. 101111, 2007.
OCBA for Simulation and Optimization
Chen, C. H., D. He, M. Fu, and L. H. Lee, "Efficient Simulation Budget Allocation for Selecting an Optimal Subset," to appear in Informs Journal on Computing, 2008.
Shi, L. and C. H. Chen, "A New Algorithm for Stochastic Discrete Resource Allocation Optimization," Journal of Discrete Event Dynamic Systems: Theory and Applications, Vol. 10, pp. 271-294, July 2000.
Applications of OCBA
Hsieh, B. W., C. H. Chen, S. C. Chang, "Efficient Simulation-based Composition of Dispatching Policies by Integrating Ordinal Optimization with Design of Experiment," IEEE Transactions on Automation Science and Engineering, Vol. 4, No. 4, pp. 553-568, October 2007.
Romero, V. J., D. V. Ayon, C. H. Chen, "Demonstration of Probabilistic Ordinal Optimization Concepts to Continuous-Variable Optimization Under Uncertainty," Optimization and Engineering, Vol. 7, No. 3, pp. 343-365, September 2006.
Chen, C. H., and D. He, "Intelligent Simulation for Alternatives Comparison and Application to Air Traffic Management," Journal of Systems Science and Systems Engineering, Vol. 14, No. 1, pp. 37-51, March 2005.
Chen, C. H., K. Donohue, E. Yücesan, and J. Lin, "Optimal Computing Budget Allocation for Monte Carlo Simulation with Application to Product Design," Journal of Simulation Practice and Theory, Vol. 11, No. 1, pp. 57-74, March 2003.
Hsieh, B. W., C. H. Chen, and S. C. Chang,
"Scheduling Semiconductor Wafer Fabrication by Using Ordinal
Optimization-Based Simulation," IEEE
Transactions on Robotics and Automation, Vol. 17, No. 5, pp. 599-608, October 2001.
Chen, C. H., S. D. Wu, and L. Dai, "Ordinal
Comparison of Heuristic Algorithms Using Stochastic Optimization," IEEE Transactions on Robotics and Automation,
Vol. 15, No. 1, pp. 44-56, February 1999.
Association with Ordinal Optimization
Dai, L., C. H. Chen, and J. R. Birge, "Large Convergence Properties of Two-Stage Stochastic Programming," Journal of Optimization Theory and Applications, Vol. 106, No. 3, pp. 489-510, September 2000.
Ho, Y. C., C. G. Cassandras, C. H. Chen, and L. Dai, "Ordinal Optimization and Simulation," Journal of Operational Research Society, Vol. 51, No. 4, pp. 490-500, April 2000.
Dai, L. and C. H. Chen, "Rate of Convergence for Ordinal Comparison of Dependent Simulations in Discrete Event Dynamic Systems," Journal of Optimization Theory and Applications, Vol. 94, No. 1, pp. 29-54, July 1997.
Go to Professor Chun-Hung Chen's Page
