Project 2: GPS, Conditioning and Nonlinear Least Squares
Brad Strylowski,
Shamaila Malik
Introduction
The global position system (GPS) is a system of 24 satellites that orbit the Earth and provide location and time information anywhere on the Earth to a
receiver that is in the line of sight of four or more of those satellites. Each of the satellites sends a signal to the receiver that is then used to
calculate the difference between the times the signal was transmitted and received. The speed of the signal is the speed of light, c=299792.458 km/sec.
The GPS receivers use these times to determine accurate (x, y, z) coordinates of the receiver. The solution to the system of four equations (one for each
satellite) and four unknowns (x, y, z, d, where d is the difference between the satellite clocks and earth-bound receiver clock) can be visualized as the
solution to the intersection of four spheres.
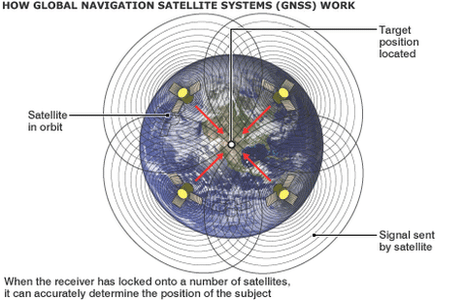
Source: BBC News Technology (http://www.bbc.co.uk/news/technology-17896353)
Solving for Location
For this project, we were asked to solve the system for the unknowns x, y, z, and d using two seperate methods. First we were asked to solve the system
using Multivariate Newtons Method and secondly by distilling the system into a single quadratic equation in terms of d and then solving using the
quadratic formula.
We were given the following positions for the four satellites (in km):
A= (15600, 7540, 20140)
B= (18760, 2750, 18610)
C= (17610, 14630, 13480)
D= (19170, 610, 18390)
And measured time intervals (in seconds):
t(A)= 0.07074
t(B)= 0.07220
t(C)= 0.07690
t(D)= 0.07242
Setting our initial vector to be (x0, y0, z0, d0)= (0, 0, 6370, 0) we created programs to solve the system using both
Multivariate Newton's Method (using the Jacobian matrix) and the
quadratic formula. In both cases we were able to confirm the expected solution of
(x, y, z)=(-41.77271, -16.78919, 6370.0596), and d=-3.201566x10^-3 seconds.
Introducing Error
Next, we redefined the satellites using polar coordinates, to allow us to readily specify the satellite's relative locations. We chose locations so that the satellites were
widely spread across the sky, and defined the user's location as x=0, y=0, z=6370, and d =.0001. Using our knowledge of the satellite's positions and the user's location,
we calculated the time for each signal to travel from the satellite to the user. After verifying our method by solving this system, we began introducing a 10^-8 second
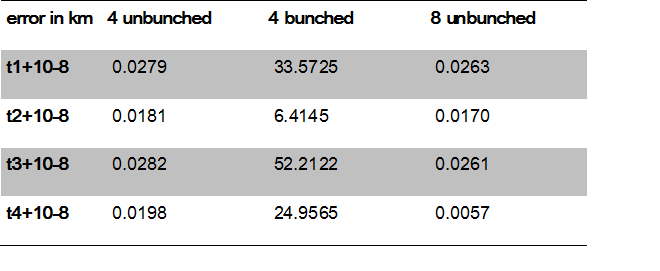
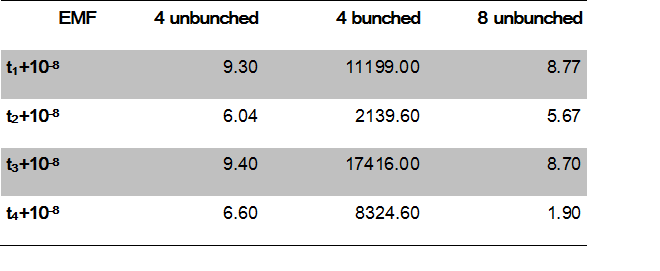
error in each of the satellites, and calculated the resulting error in the final solution and the problem's error magnification factor. For the unbunched satellites,
the EMF remained small, and all were less than 10. Our largest absolute error occurred when we added 10^-8 seconds to the time from the third satellite, and the error was
approximately 28 m. Judging by the magnitude of the various EMFs, the condition number for this system was probably close to 10.
Regrouped Satellites
We redefined the satellites' positions to a more tightly bunched configuration, with each satellite within 5% angular distance of each other. We solved the system both with
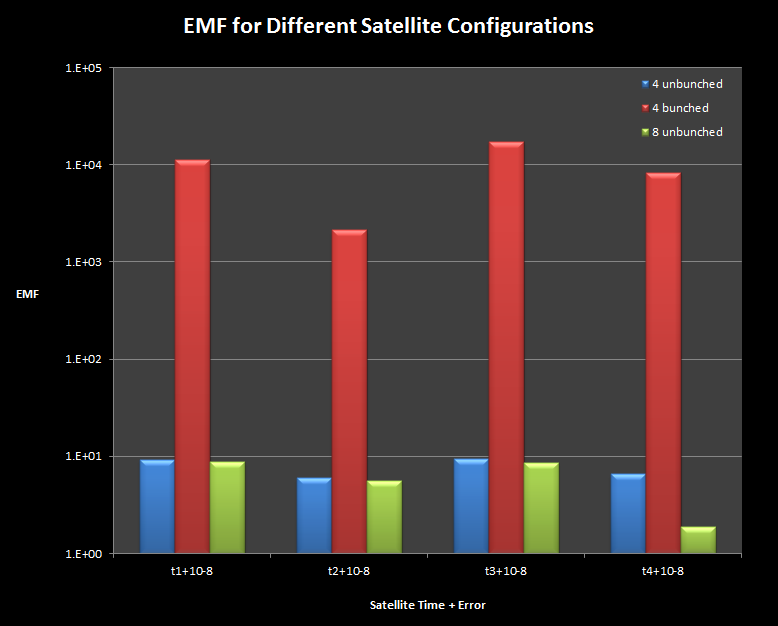
and without the errors introduced in the previous section. With tightly grouped satellites, both the position error and the EMF increased drastically, with EMFs on the order
of 10^3 or 10^4 and position errors as large as 52 km. Our estimate of the problem's condition number was 17500, much larger than the previous section's.
Additional Satellites
In an attempt to improve our solution by adding more information, we added four extra satellites to the system and returned them to the unbunched configuration. This required
rewriting our solution as a Gauss-Newton Iteration of a least squares system with more equations than unknowns. In the context of this problem, the most reasonable initial
position vector would be the same as the solution of the previous system, as GPS data must be updated continuously. When we reintroduced the error to the system, our EMF and
absolute error remained slightly less than the four unbunched satellites', with a maximum error of 26 m. The condition number of the least-squares system was about 9. Our
results demonstrated that unbunched satellites produced more reliable solutions with small errors, and with more than four satellites above the horizon, errors caused by
satellite signals should not affect the position by more than 1 km.
Data