Introduction: This project uses the Distrete Cosine
Function to compress images. We use it to change the number of bits
needed to show an image with minimal loss of clarity in the image. We
explore the effects of different quantization matrices,Q and Qy, and
scalars, p, to see how they affect the quality of the image. To
examine the influences of these parameters on a 256 x 256 pixel image, I
did computer problems 3-6 from Numerical Analysis.
3. a) First, I took an 8 by 8 pixel part of the whole image, and
displayed it in MATLAB.
b) In the next part, I took the 2D-DCT of the 8 by 8 pixel image, using dct.m and proj_5.m , and
compared it with the original 8 by 8 image.
c) Then, I quantize the 8 by 8 image with the matrix, Q,
using Quantization.m and differing values of
p (1,2, and 4).
d) We compared the compared the compressed image with the
original for each value of p.
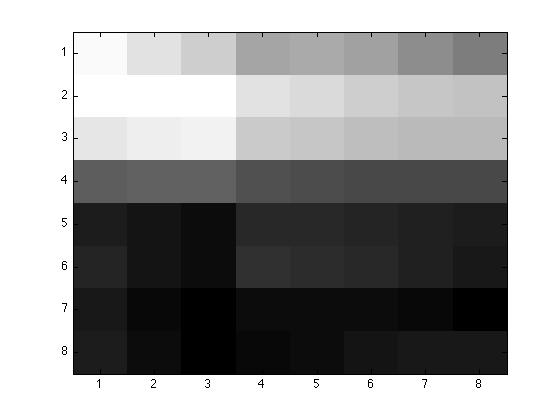
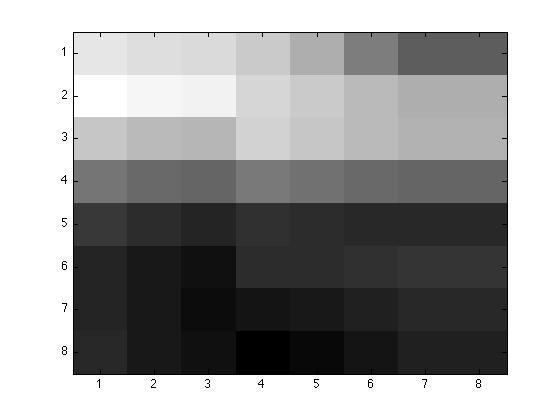
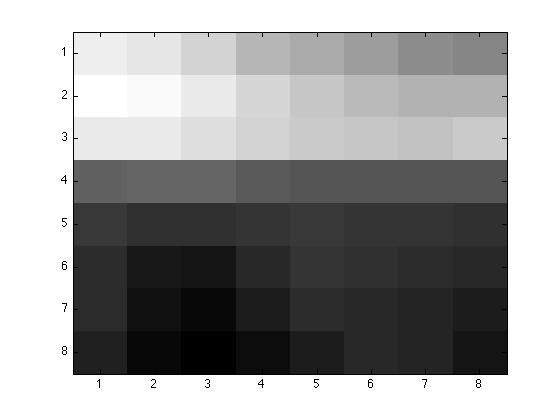
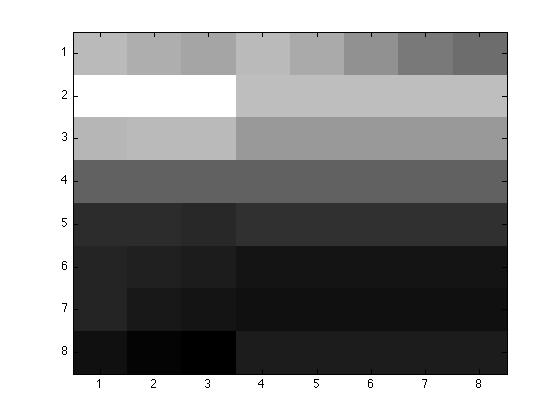Original 8 by 8 chunk, p=1, p=2, and p=4.
Original 8 by 8 chunk, p=1, p=2, and p=4.
e) Finally, we reconsitute the image for each value of p, and
compare with the original image.
Original image, p=1, p=2, and p=4.
Original image, p=1, p=2, and p=4.
4. In the next part, we quantize using a different quantization matrix,
Qy. We compare these results with the original image. Below are the
results for p = 1.
Original image, quantization with Qy matrix and p=1.
Original image, quantization with Qy matrix and p=1.
5. In the next part, I basically repeated the process from part 3, only I
performed the quantization on each of the three color layers of the image,
the red, green and blue colors, separately, and then recombined each 8 by
8 block into the original image. For this, I used the ColorQuantization.m code. I did this for
p values of 1, 2 and 4.
Original image, color-quantized image with p=1, p=2,
and p=4.
Original image, color-quantized image with p=1, p=2,
and p=4.
6. For the last part, I had to transform the RGB colors to luminance,Y,
and color difference coordinates U and V. After performing quantization
with luminance.m, I recombined the RGB parts
of the picture with different p values of 1, 2 and 4. Finally, I
compared these results with the original color image.
Original image, luminance quantization with p=1, p=2,
and p=4.
Original image, luminance quantization with p=1, p=2,
and p=4.
Conclusion: I was able to see how an image can be
compressed using different quantization methods and matrices, and see also
how small changes on the quantization matrix could have a significant
effect on the quality of the image being displayed.