Project 6: Google Page Rank and Eigenvectors
Aidan Curran
Contents
Background
Google page rank and eigenvectors Short Version
Eigenvalues and Singular Values Longer Version, Chapter 12 from Numerical Analysis textbook
**** This project is the shortened version ****
Problem 1
Find the adjacency matrix A and google matrix G for the following internet graph. Give the page rank vector, and rank all of the pages, from most to least important, according to page rank.
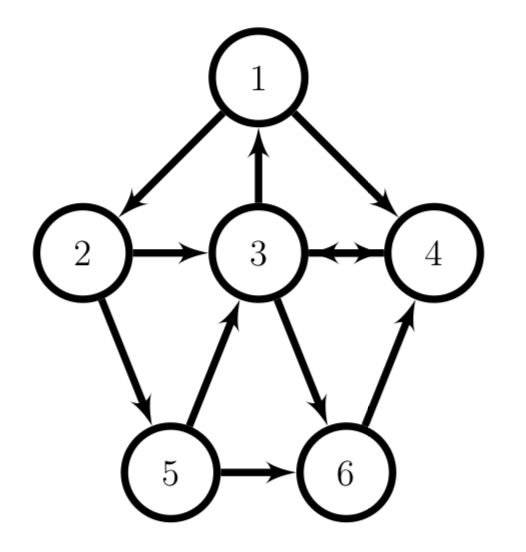
This is the adjacency matrix for the grpah above
A=[0 0 1 0 0 0 1 0 0 0 0 0; 0 1 0 1 1 0; 1 0 1 0 0 1; 0 1 0 0 0 0; 0 0 1 0 1 0]
A =
0 0 1 0 0 0
1 0 0 0 0 0
0 1 0 1 1 0
1 0 1 0 0 1
0 1 0 0 0 0
0 0 1 0 1 0
D=diag(sum(A,1))
D =
2 0 0 0 0 0
0 2 0 0 0 0
0 0 3 0 0 0
0 0 0 1 0 0
0 0 0 0 2 0
0 0 0 0 0 1
G=A*inv(D)
G =
0 0 0.3333 0 0 0
0.5000 0 0 0 0 0
0 0.5000 0 1.0000 0.5000 0
0.5000 0 0.3333 0 0 1.0000
0 0.5000 0 0 0 0
0 0 0.3333 0 0.5000 0
[eigvec,eigval]=eig(G)
eigvec = Columns 1 through 4 -0.2327 + 0.0000i -0.1695 - 0.2357i -0.1695 + 0.2357i -0.1440 + 0.2566i -0.1163 + 0.0000i -0.0582 + 0.1734i -0.0582 - 0.1734i 0.1955 + 0.3340i -0.6981 + 0.0000i 0.6914 + 0.0000i 0.6914 + 0.0000i -0.3357 + 0.0061i -0.6108 + 0.0000i -0.3463 + 0.3758i -0.3463 - 0.3758i -0.4187 - 0.2760i -0.0582 + 0.0000i 0.1101 - 0.0340i 0.1101 + 0.0340i 0.5089 + 0.0000i -0.2618 + 0.0000i -0.2274 - 0.2795i -0.2274 + 0.2795i 0.1940 - 0.3208i Columns 5 through 6 -0.1440 - 0.2566i -0.4106 + 0.0000i 0.1955 - 0.3340i 0.4488 + 0.0000i -0.3357 - 0.0061i 0.5634 + 0.0000i -0.4187 + 0.2760i -0.2368 + 0.0000i 0.5089 + 0.0000i -0.4906 + 0.0000i 0.1940 + 0.3208i 0.1258 + 0.0000i eigval = Columns 1 through 4 1.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.4634 + 0.6444i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.4634 - 0.6444i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.1921 + 0.3281i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i Columns 5 through 6 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.1921 - 0.3281i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.4574 + 0.0000i
v=eigvec(:,1)
v = -0.2327 -0.1163 -0.6981 -0.6108 -0.0582 -0.2618
v=v/sum(v)
v =
0.1176
0.0588
0.3529
0.3088
0.0294
0.1324
Page Ranks:
- Node 3 has the highest page rank
- node 4
- node 6
- node 1
- node 2
- node 5
Adding the vector values from v should equal 1
check = sum(v)
check =
1.0000
Problem 2
Same as Problem 1, for the following graph.
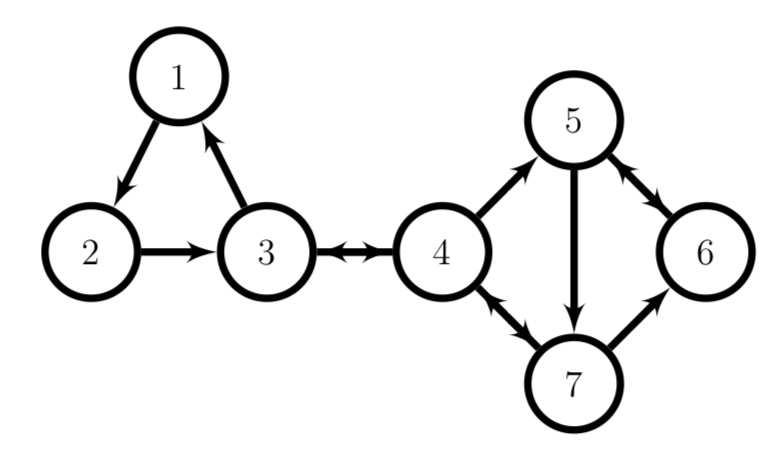
B=[0 0 1 0 0 0 0 1 0 0 0 0 0 0; 0 1 0 1 0 0 0; 0 0 1 0 0 0 1; 0 0 0 1 0 1 0; 0 0 0 0 1 0 1; 0 0 0 1 1 0 0]
B =
0 0 1 0 0 0 0
1 0 0 0 0 0 0
0 1 0 1 0 0 0
0 0 1 0 0 0 1
0 0 0 1 0 1 0
0 0 0 0 1 0 1
0 0 0 1 1 0 0
D=diag(sum(B,1))
D =
1 0 0 0 0 0 0
0 1 0 0 0 0 0
0 0 2 0 0 0 0
0 0 0 3 0 0 0
0 0 0 0 2 0 0
0 0 0 0 0 1 0
0 0 0 0 0 0 2
G=B*inv(D)
G =
0 0 0.5000 0 0 0 0
1.0000 0 0 0 0 0 0
0 1.0000 0 0.3333 0 0 0
0 0 0.5000 0 0 0 0.5000
0 0 0 0.3333 0 1.0000 0
0 0 0 0 0.5000 0 0.5000
0 0 0 0.3333 0.5000 0 0
[eigvec,eigval]=eig(G)
eigvec = Columns 1 through 4 -0.1043 + 0.0000i 0.2879 + 0.0000i -0.2144 - 0.3340i -0.2144 + 0.3340i -0.1043 + 0.0000i 0.3488 + 0.0000i -0.2208 + 0.4822i -0.2208 - 0.4822i -0.2085 + 0.0000i 0.4754 + 0.0000i 0.5941 + 0.0000i 0.5941 + 0.0000i -0.3128 + 0.0000i 0.1310 + 0.0000i -0.0583 - 0.3239i -0.0583 + 0.3239i -0.6255 + 0.0000i -0.5151 + 0.0000i -0.0862 - 0.1115i -0.0862 + 0.1115i -0.5213 + 0.0000i -0.4689 + 0.0000i 0.1245 + 0.0988i 0.1245 - 0.0988i -0.4170 + 0.0000i -0.2591 + 0.0000i -0.1390 + 0.1885i -0.1390 - 0.1885i Columns 5 through 7 -0.0108 + 0.0877i -0.0108 - 0.0877i -0.0458 + 0.0000i 0.0795 - 0.0956i 0.0795 + 0.0956i -0.2566 + 0.0000i -0.0544 - 0.1131i -0.0544 + 0.1131i -0.0164 + 0.0000i -0.0107 + 0.4270i -0.0107 - 0.4270i 0.7610 + 0.0000i 0.6301 + 0.0000i 0.6301 + 0.0000i -0.4044 + 0.0000i -0.3731 + 0.0996i -0.3731 - 0.0996i -0.3259 + 0.0000i -0.2607 - 0.4055i -0.2607 + 0.4055i 0.2881 + 0.0000i eigval = Columns 1 through 4 1.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.8255 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.4043 + 0.6298i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.4043 - 0.6298i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i Columns 5 through 7 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.5977 + 0.3839i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.5977 - 0.3839i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.1785 + 0.0000i
v=eigvec(:,1)
v = -0.1043 -0.1043 -0.2085 -0.3128 -0.6255 -0.5213 -0.4170
v=v/sum(v)
v =
0.0455
0.0455
0.0909
0.1364
0.2727
0.2273
0.1818
Page Ranks:
- Node 5 has the highest page rank
- node 6
- node 7
- node 4
- node 3
- node 1 and node 2
Adding the vector values from v should equal 1
check = sum(v)
check =
1
Problem 3
Make your own graph and find page ranks.
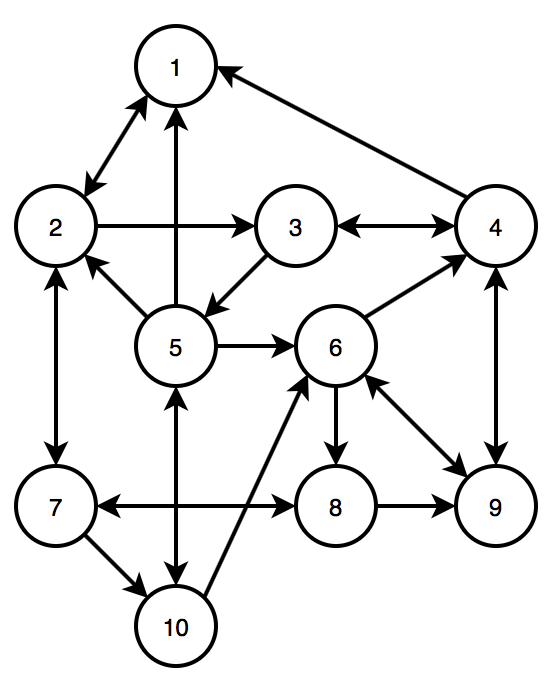
C=[0 1 0 1 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0; 0 1 0 1 1 0 0 0 0 0; 0 0 1 0 0 1 0 0 1 0; 0 0 1 0 0 0 0 0 0 1; 0 0 0 0 1 0 0 0 1 1; 0 1 0 0 0 0 0 1 0 0; 0 0 0 0 0 1 1 0 0 0; 0 0 0 1 0 1 0 1 0 0; 0 0 0 0 0 0 1 0 0 0]
C =
0 1 0 1 1 0 0 0 0 0
1 0 0 0 0 0 1 0 0 0
0 1 0 1 1 0 0 0 0 0
0 0 1 0 0 1 0 0 1 0
0 0 1 0 0 0 0 0 0 1
0 0 0 0 1 0 0 0 1 1
0 1 0 0 0 0 0 1 0 0
0 0 0 0 0 1 1 0 0 0
0 0 0 1 0 1 0 1 0 0
0 0 0 0 0 0 1 0 0 0
D=diag(sum(C,1))
D =
1 0 0 0 0 0 0 0 0 0
0 3 0 0 0 0 0 0 0 0
0 0 2 0 0 0 0 0 0 0
0 0 0 3 0 0 0 0 0 0
0 0 0 0 3 0 0 0 0 0
0 0 0 0 0 3 0 0 0 0
0 0 0 0 0 0 3 0 0 0
0 0 0 0 0 0 0 2 0 0
0 0 0 0 0 0 0 0 2 0
0 0 0 0 0 0 0 0 0 2
G=C*inv(D)
G =
Columns 1 through 7
0 0.3333 0 0.3333 0.3333 0 0
1.0000 0 0 0 0 0 0.3333
0 0.3333 0 0.3333 0.3333 0 0
0 0 0.5000 0 0 0.3333 0
0 0 0.5000 0 0 0 0
0 0 0 0 0.3333 0 0
0 0.3333 0 0 0 0 0
0 0 0 0 0 0.3333 0.3333
0 0 0 0.3333 0 0.3333 0
0 0 0 0 0 0 0.3333
Columns 8 through 10
0 0 0
0 0 0
0 0 0
0 0.5000 0
0 0 0.5000
0 0.5000 0.5000
0.5000 0 0
0 0 0
0.5000 0 0
0 0 0
[eigvec,eigval]=eig(G)
eigvec = Columns 1 through 4 -0.4218 + 0.0000i -0.3726 + 0.0000i -0.0200 + 0.0878i -0.0200 - 0.0878i 0.5855 + 0.0000i -0.4513 + 0.0000i -0.1129 - 0.0399i -0.1129 + 0.0399i -0.4218 + 0.0000i -0.3726 + 0.0000i -0.0200 + 0.0878i -0.0200 - 0.0878i 0.3547 + 0.0000i -0.4410 + 0.0000i -0.2154 - 0.0115i -0.2154 + 0.0115i 0.1776 + 0.0000i -0.2256 + 0.0000i 0.3027 - 0.0799i 0.3027 + 0.0799i -0.0196 + 0.0000i -0.2769 + 0.0000i -0.4233 - 0.2458i -0.4233 + 0.2458i -0.2863 + 0.0000i -0.2359 + 0.0000i 0.2374 - 0.2773i 0.2374 + 0.2773i 0.1154 + 0.0000i -0.1709 + 0.0000i -0.0283 + 0.3728i -0.0283 - 0.3728i -0.1918 + 0.0000i -0.3248 + 0.0000i 0.5018 + 0.0000i 0.5018 + 0.0000i 0.1080 + 0.0000i -0.0786 + 0.0000i -0.2218 + 0.1059i -0.2218 - 0.1059i Columns 5 through 8 -0.0482 + 0.0000i 0.0618 - 0.0440i 0.0618 + 0.0440i 0.0000 + 0.0000i 0.5036 + 0.0000i -0.1428 + 0.0590i -0.1428 - 0.0590i -0.3586 + 0.0000i -0.0482 + 0.0000i 0.0618 - 0.0440i 0.0618 + 0.0440i 0.2390 + 0.0000i 0.0354 + 0.0000i -0.3945 - 0.0186i -0.3945 + 0.0186i -0.3586 + 0.0000i -0.4967 + 0.0000i 0.5780 + 0.0000i 0.5780 + 0.0000i 0.7171 + 0.0000i 0.4397 + 0.0000i 0.3738 - 0.0108i 0.3738 + 0.0108i -0.0000 + 0.0000i -0.2981 + 0.0000i -0.2478 + 0.0332i -0.2478 - 0.0332i -0.0000 + 0.0000i -0.1610 + 0.0000i 0.0576 - 0.1594i 0.0576 + 0.1594i 0.2390 + 0.0000i -0.2657 + 0.0000i -0.3356 - 0.1462i -0.3356 + 0.1462i -0.2390 + 0.0000i 0.3392 + 0.0000i -0.0124 + 0.3308i -0.0124 - 0.3308i -0.2390 + 0.0000i Columns 9 through 10 0.0765 + 0.1475i 0.0765 - 0.1475i 0.3616 + 0.1988i 0.3616 - 0.1988i 0.0765 + 0.1475i 0.0765 - 0.1475i -0.5332 + 0.0000i -0.5332 + 0.0000i 0.2462 + 0.0422i 0.2462 - 0.0422i -0.1856 - 0.1462i -0.1856 + 0.1462i 0.2571 - 0.0483i 0.2571 + 0.0483i 0.0236 - 0.1345i 0.0236 + 0.1345i -0.4837 - 0.1457i -0.4837 + 0.1457i 0.1610 - 0.0613i 0.1610 + 0.0613i eigval = Columns 1 through 4 -0.8834 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 1.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.4525 + 0.2006i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.4525 - 0.2006i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i Columns 5 through 8 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.2930 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0428 + 0.2481i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0428 - 0.2481i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i -0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i Columns 9 through 10 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.4979 + 0.0897i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.4979 - 0.0897i
v=eigvec(:,2)
v = -0.3726 -0.4513 -0.3726 -0.4410 -0.2256 -0.2769 -0.2359 -0.1709 -0.3248 -0.0786
v=v/sum(v)
v =
0.1263
0.1530
0.1263
0.1495
0.0765
0.0939
0.0800
0.0579
0.1101
0.0267
Page Ranks:
- Node 2 has the highest page rank
- node 4
- node 1 and node 3
- node 9
- node 6
- node 7
- node 5
- node 8
- node 10
Adding the vector values from v should equal 1
check = sum(v)
check =
1