MATH 447 Project 5
A Simple Audio Codec
Instructions and background information for project 5
SimpleCodec without Windowing
SimpleCodec with Windowing
Script Problem 2
Script Problem 5
Ahmad Amin
Background information
For this reality check, a modified discrete cosine transform (MDCT) was used along with bit quantization in order to compress audio signals. The MDCT was applied
to a window of 2n signal values and and a frequency of n. Compression is performmed after bit quantization was performed in order to save space.
Problem 1.)
SimpleCodec No Windowing
For problem 1, the simplecodec file was run with a simple pure tone. Bits were initialized to b=4/window, window size was set to n=32, and
a random frequency was chosen between 100 and 1000 (h=600hZ). The initial tone was constructed with the input signal of (cos((1:2^(13))*2*pi*600/2^(13)))')
After creating the tone without a windowing effect, the RMSE was calculated to be 0.0270372104814203
The plot below plots the original and compressed output signals on the same plot.
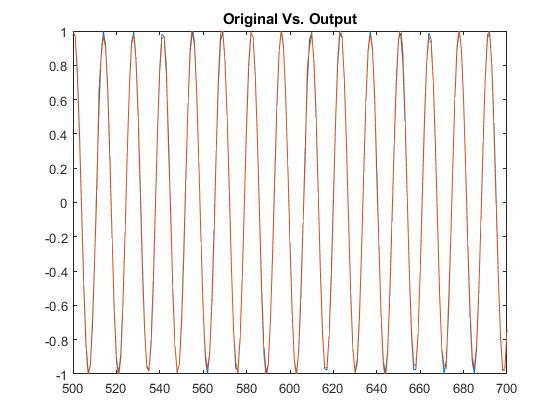
Problem 2.)
Script
For this problem, different chords were were constructed and evaluated (but they were not overlapped).
No Windowing and Octave (produced with a 2:1 ratio of frequencies):
\begin{array} {|l|l|}\hline
Quantization\ Bits & RMSE \\ \hline
1 & 0.171453028728139 \\ \hline
2 & 0.095169057262069 \\ \hline
3 & 0.055883355845638 \\ \hline
4 & 0.029438378517373 \\ \hline
5 & 0.013105562702497 \\ \hline
6 & 0.006503132531126 \\ \hline
7 & 0.003269422780384 \\ \hline
8 & 0.001572072434962\\ \hline
\end{array}
No Windowing and a Third (produced with a 1.25:1 ratio of frequencies):
\begin{array} {|l|l|}\hline
Quantization\ Bits & RMSE \\ \hline
1 & 0.247969412819361 \\ \hline
2 & 0.122835897068855 \\ \hline
3 & 0.063102417761673 \\ \hline
4 & 0.027013795252306 \\ \hline
5 & 0.013105562702497 \\ \hline
6 & 0.006416906268538 \\ \hline
7 & 0.003272901159013 \\ \hline
8 & 0.001600274409065 \\ \hline
\end{array}
No Windowing and a Fifth (produced with a 1.5:1 ratio of frequencies):
\begin{array} {|l|l|}\hline
Quantization\ Bits & RMSE \\ \hline
1 & 0.263637983106537\\ \hline
2 & 0.130067449441666\\ \hline
3 & 0.061591400911847\\ \hline
4 & 0.028237755817176\\ \hline
5 & 0.013113741879127\\ \hline
6 & 0.006439955089788\\ \hline
7 & 0.003248573156387\\ \hline
8 & 0.001597213157237\\ \hline
\end{array}
As Evident, each differnt constructed chord displays the same pattern where an increase in the number of quantized bits per window results in a decrease in RMSE. In general, it also appears that the compressed octave produces a relatively lower RMSE compared to a third and a fifth, and a fifth produces relatively higher RMSEs.
*Note: These RMSEs were calculated with a frequency of 600 hZ for a simple signal of (cos((1:2^(13))*2*pi*600*ratio/2^(13)))') where ratio was the ratio used to compute the different Octaves.
Problem 3.)
SimpleCodec With Windowing
For problem 3, a windowing fnction was applied to reduce codec error. This function scaled the input signal to smoothen the ends to eliminate the problem that the initial signal represented is not periodic over the window. In order to demonstrate the differences between windowing and no windowing, the same chords as above were reproduced, except this time with a windowing function.
No Windowing and Octave (produced with a 2:1 ratio of frequencies):
\begin{array} {|l|l|}\hline
Quantization\ Bits & RMSE \\ \hline
1 & 0.154167998730922 \\ \hline
2 & 0.065964093751279 \\ \hline
3 & 0.034512434394393\\ \hline
4 & 0.018623956663237\\ \hline
5 & 0.010809116454476\\ \hline
6 & 0.005570063986312\\ \hline
7 & 0.003080511379930\\ \hline
8 & 0.001595193440997\\ \hline
\end{array}
No Windowing and a Third (produced with a 1.25:1 ratio of frequencies):
\begin{array} {|l|l|}\hline
Quantization\ Bits & RMSE \\ \hline
1 & 0.111342389751106\\ \hline
2 & 0.055308323655447\\ \hline
3 & 0.028441834270263\\ \hline
4 & 0.015458434369766\\ \hline
5 & 0.008749156160073\\ \hline
6 & 0.004619631759946\\ \hline
7 & 0.002575399793014\\ \hline
8 & 0.001425964642907\\ \hline
\end{array}
No Windowing and a Fifth (produced with a 1.5:1 ratio of frequencies):
\begin{array} {|l|l|}\hline
Quantization\ Bits & RMSE \\ \hline
1 & 0.105055925786775\\ \hline
2 & 0.037323702127601\\ \hline
3 & 0.018680594896186\\ \hline
4 & 0.011771575474961\\ \hline
5 & 0.006405947103487\\ \hline
6 & 0.003684668355045\\ \hline
7 & 0.002125383951728\\ \hline
8 & 0.001202474415905\\ \hline
\end{array}
Plots below compare RMSE's between different chords and differing # of bits user per window for bit quantization for both windowing and no windowing:
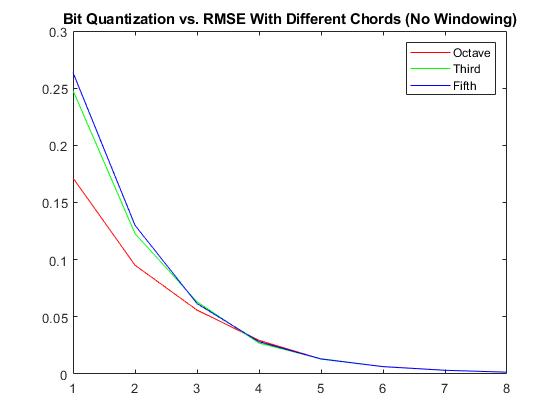
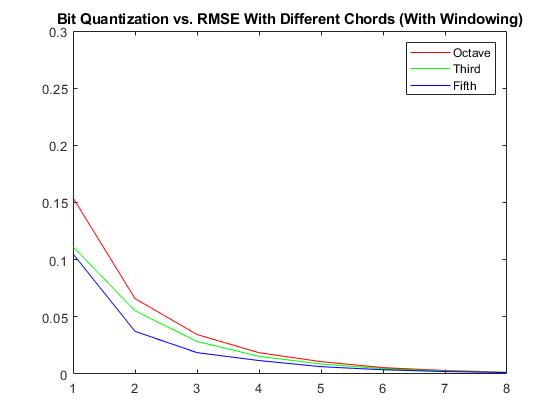
Problem 4.)
Windowing Function
Z1 and Z2 are 2n-vectors where the last half of Z1 overlaps with Z2.
Problem 5.)
SimpleCodec without Windowing
SimpleCodec with Windowing
Script Problem 5
For problem 5, I reconstructed the first few seconds of the Game of Thrones Theme Song by Ramin Djawadi. I did this by comparing the RMSE's of quantization bits of 1-8 for both simplecodec with and without the windowing function.
The initial audio I downloaded from the internet:
With a quantization bit of b=1, RMSE without windowing was 0.0878143936932681 and with windowing was 0.0822777373514979. The Plots below display the differences between original signal and produced signal for both windowing and non-windowing simpleCodec functions:
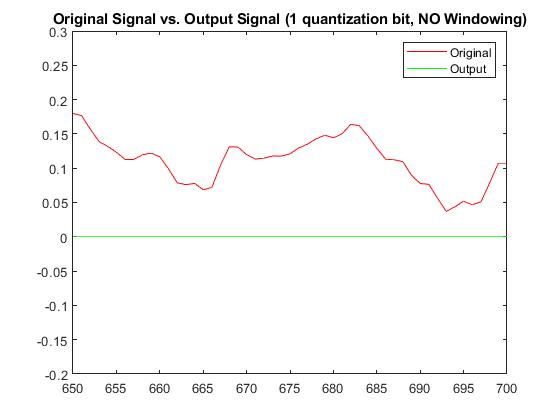
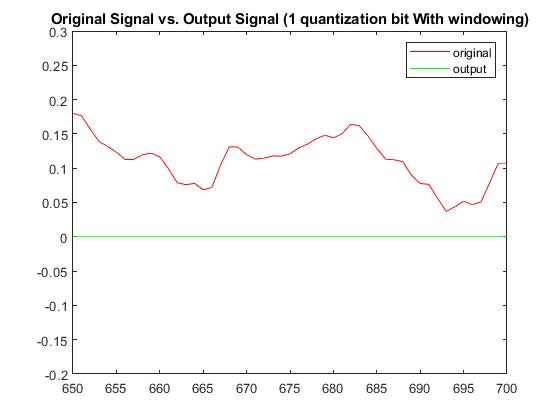
Audio (1-bit quantization; No-windowing):
Audio (1-bit quantization; With windowing):
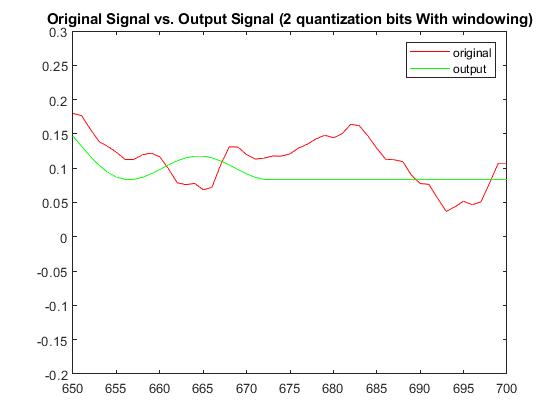
With a quantization bit of b=2, RMSE without windowing was 0.04715143878519 and with windowing was 0.0382730656893698. The Plots below display the differences between original signal and produced signal for both windowing and non-windowing simpleCodec functions:
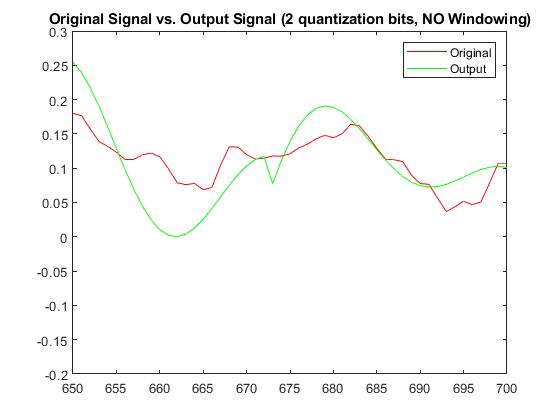
Audio (2-bit quantization; No-windowing):
Audio (2-bit quantization; With windowing):
With a quantization bit of b=3, RMSE without windowing was 0.029411931492528 and with windowing was 0.0207357744359836. The Plots below display the differences between original signal and produced signal for both windowing and non-windowing simpleCodec functions:
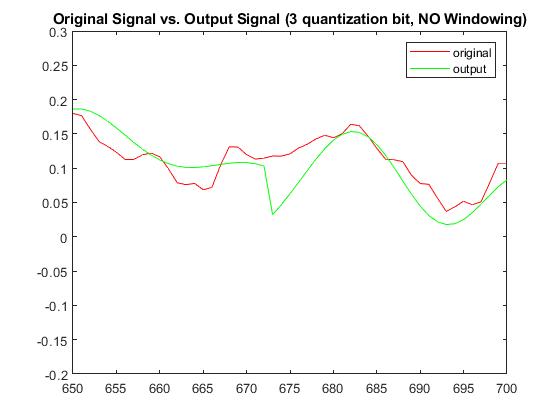
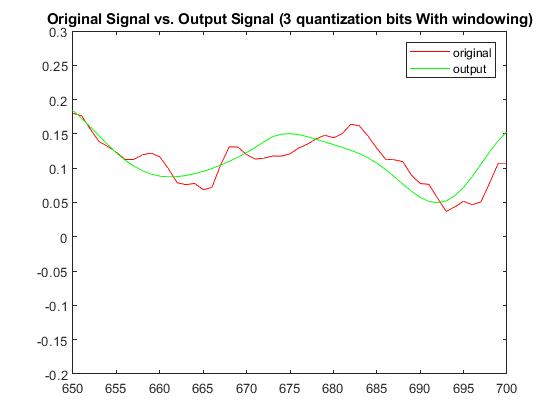
Audio (3-bit quantization; No-windowing):
Audio (3-bit quantization; With windowing):
With a quantization bit of b=4, RMSE without windowing was 0.0194151284490152 and with windowing was 0.0115127793439055. The Plots below display the differences between original signal and produced signal for both windowing and non-windowing simpleCodec functions:
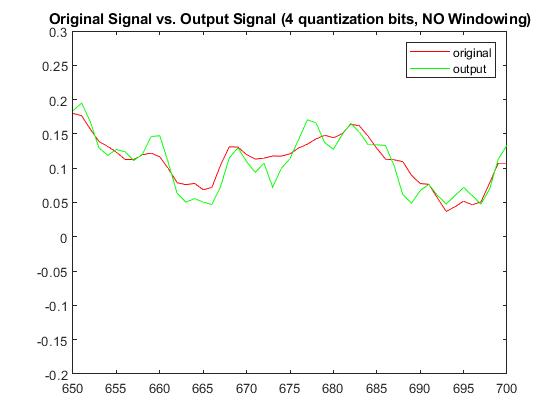
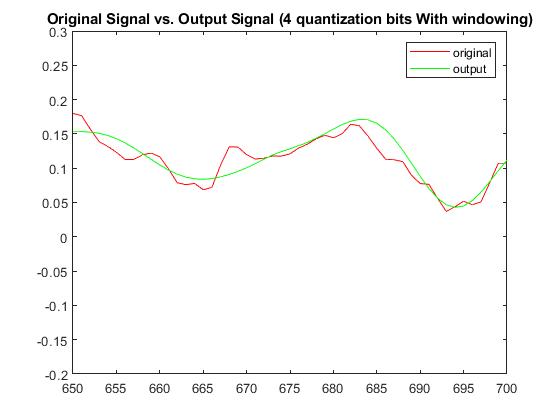
Audio (4-bit quantization; No-windowing):
Audio (4-bit quantization; With windowing):
With a quantization bit of b=5, RMSE without windowing was 0.0121669466894805 and with windowing was 0.00675740044843647. The Plots below display the differences between original signal and produced signal for both windowing and non-windowing simpleCodec functions:
Audio (5-bit quantization; No-windowing):
Audio (5-bit quantization; With windowing):
With a quantization bit of b=6, RMSE without windowing was 0.00644879139492435 and with windowing was 0.00407707490017487. The Plots below display the differences between original signal and produced signal for both windowing and non-windowing simpleCodec functions:
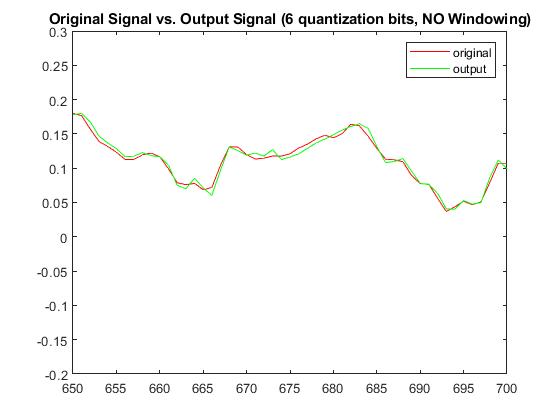
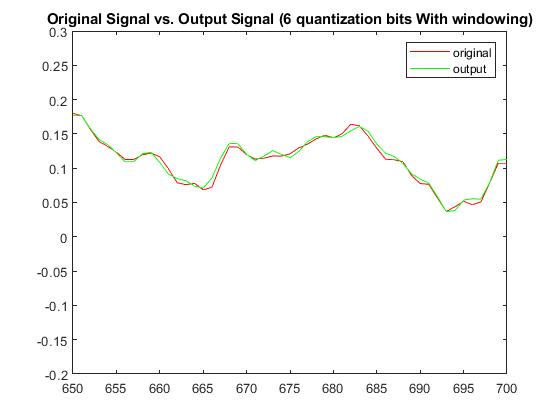
Audio (6-bit quantization; No-windowing):
Audio (6-bit quantization; With windowing):
With a quantization bit of b=8, RMSE without windowing was 0.00160114157313961 and with windowing was 0.00131969706498556. The Plots below display the differences between original signal and produced signal for both windowing and non-windowing simpleCodec functions:
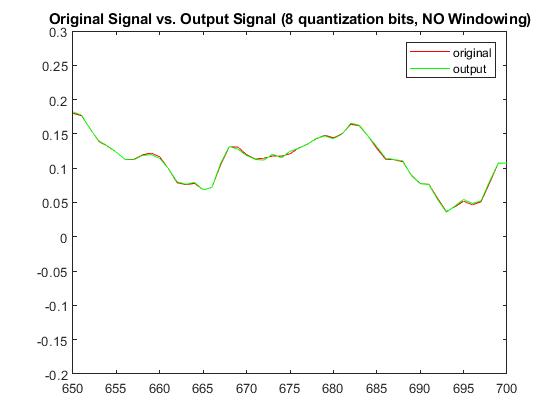
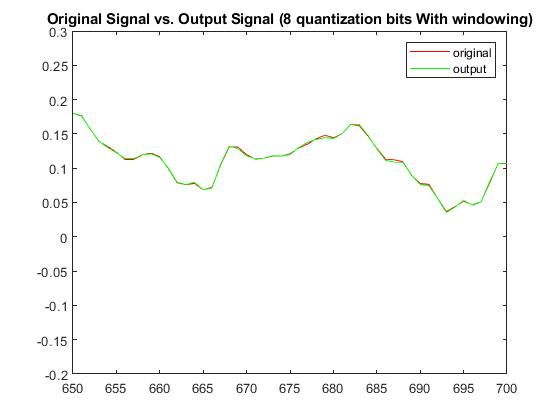
A final plot that displays the relationships between RMSE when a windowing function is applied / also when the number of bits changes is seen below from a range of 1 to 8 bits:
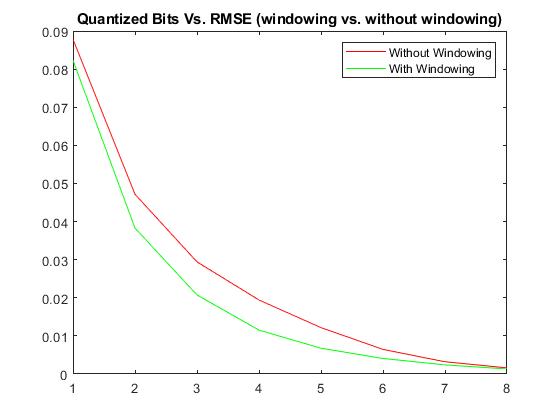
Conclusion
In general, increases in the bit quantization for both windowing and non-windowing shows reduced errors (RMSE) and eventually the application
of the windwowing function is trivial. In the future, I would reproduce problems 1 and 2 with actual chords (for instance 600 hZ is fairly close to 622 hZ which
is a D-Sharp Chord. Also for problem 2 I would play overlapping chords.