Project 1
Kinematics of the Stewart Platform
Vincent Caetto, Robert Argus, Hannah Andrada
1. Write a Matlab function file for \(f(\theta)\). The parameters \(L_1, L_2, L_3, \gamma, x_1, x_2, y_2\) are fixed constants, and the strut lengths \(p_1,p_2,p_3\) will be known for a given pose. To test your code, set the parameters \(L_1 = 2, L_2 = L_3 = \sqrt 2, \gamma = \frac{p}{2} , p_1 = p_2 = p_3 = \sqrt 5\) from Figure 1.15. Then, substituting \(\theta = -\frac{p}{4}\) or \( \theta = \frac{p}{4}\), corresponding to Figures 1.15(a, b), respectively, should make \(f(\theta) = 0\).
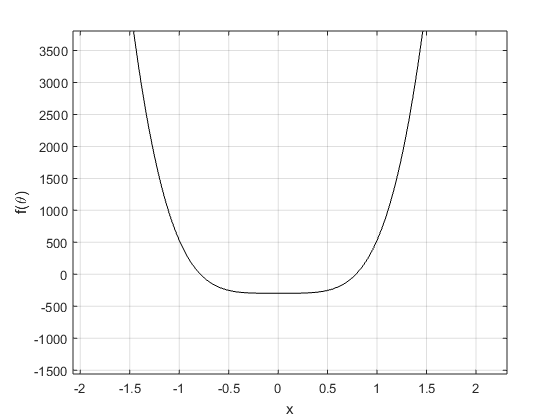
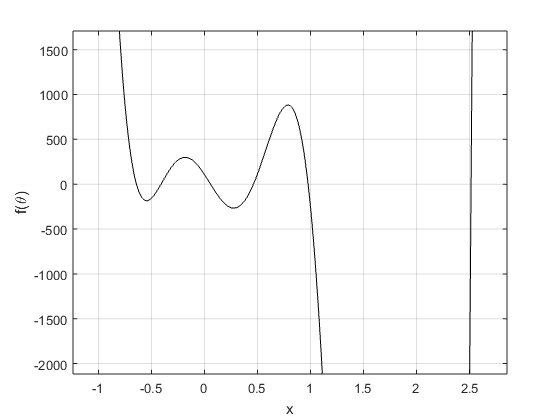
2. Plot f\((\theta)\) on \([-\pi,\pi]\). As a check of your work, there should be roots at \(\pm\frac{\pi}{4}\).
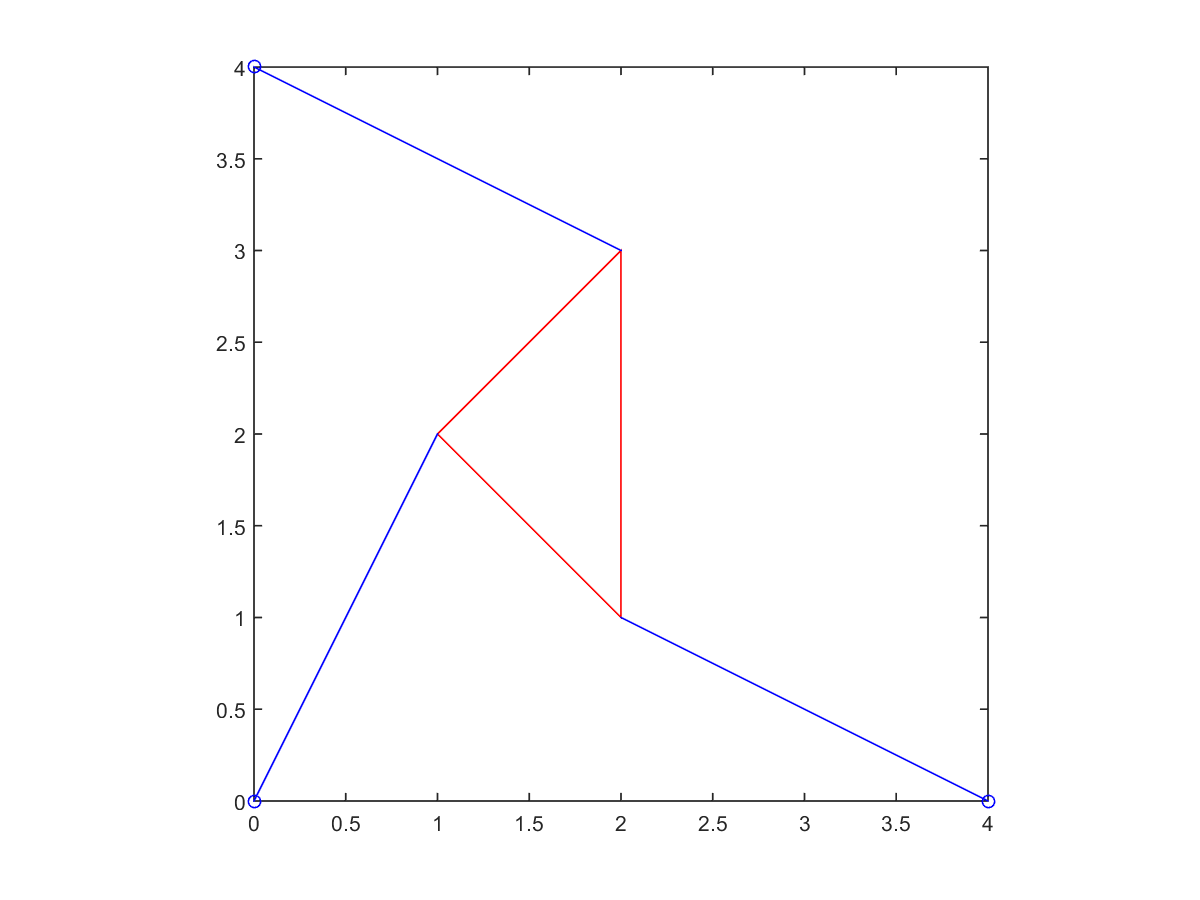
3. Reproduce Figure 1.15. The Matlab commands
>> plot([u1 u2 u3 u1],[v1 v2 v3 v1],'r'); hold on
>> plot([0 x1 x2],[0 0 y2],'bo'
will plot a red triangle with vertices (u1,v1),(u2,v2),(u3,v3) and
place small
circles at the strut anchor points (0,0),(0,x1),(x2,y2). In addition, draw the
struts.
 |
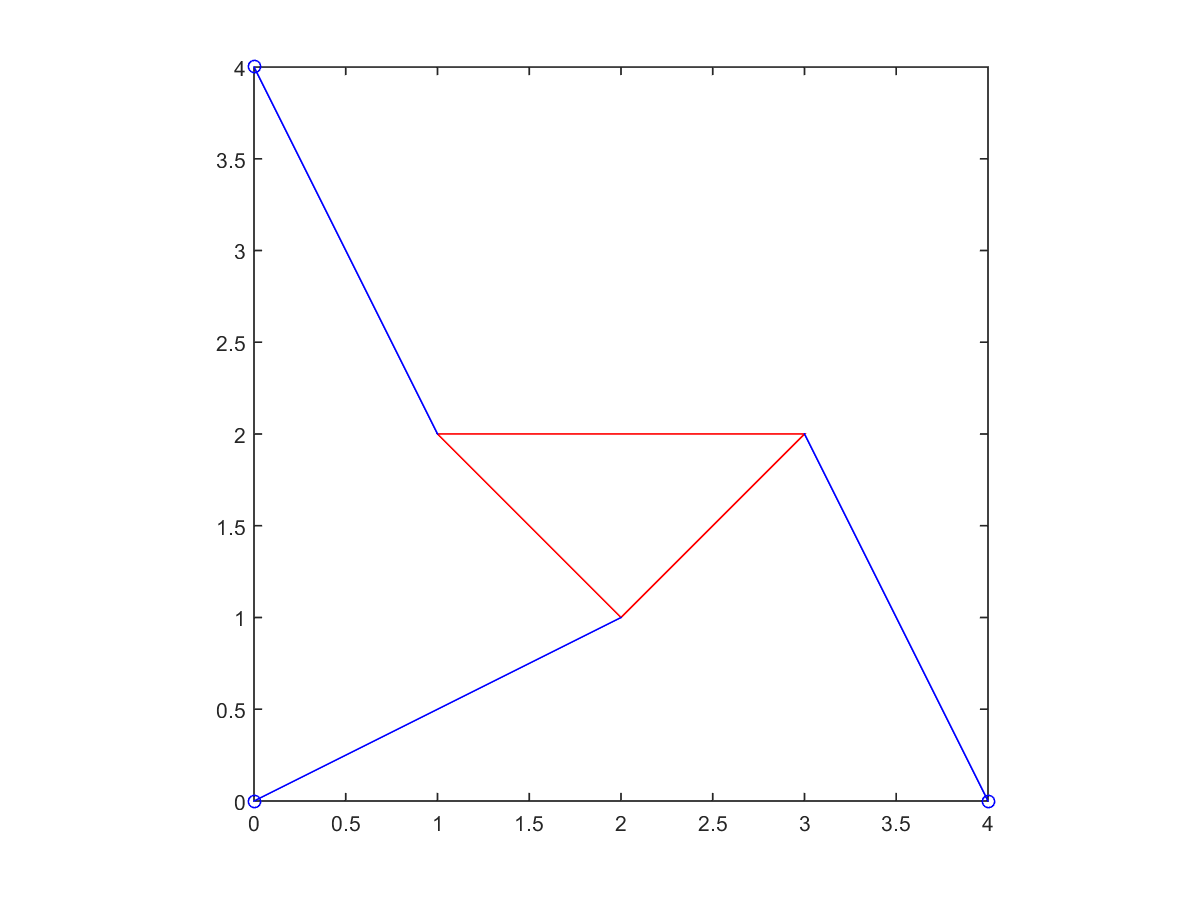 |
| Root at \(\frac{\pi}{4}\) | Root at \(-\frac{\pi}{4}\) |
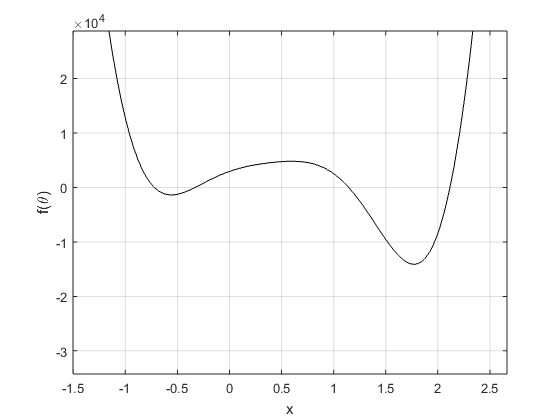
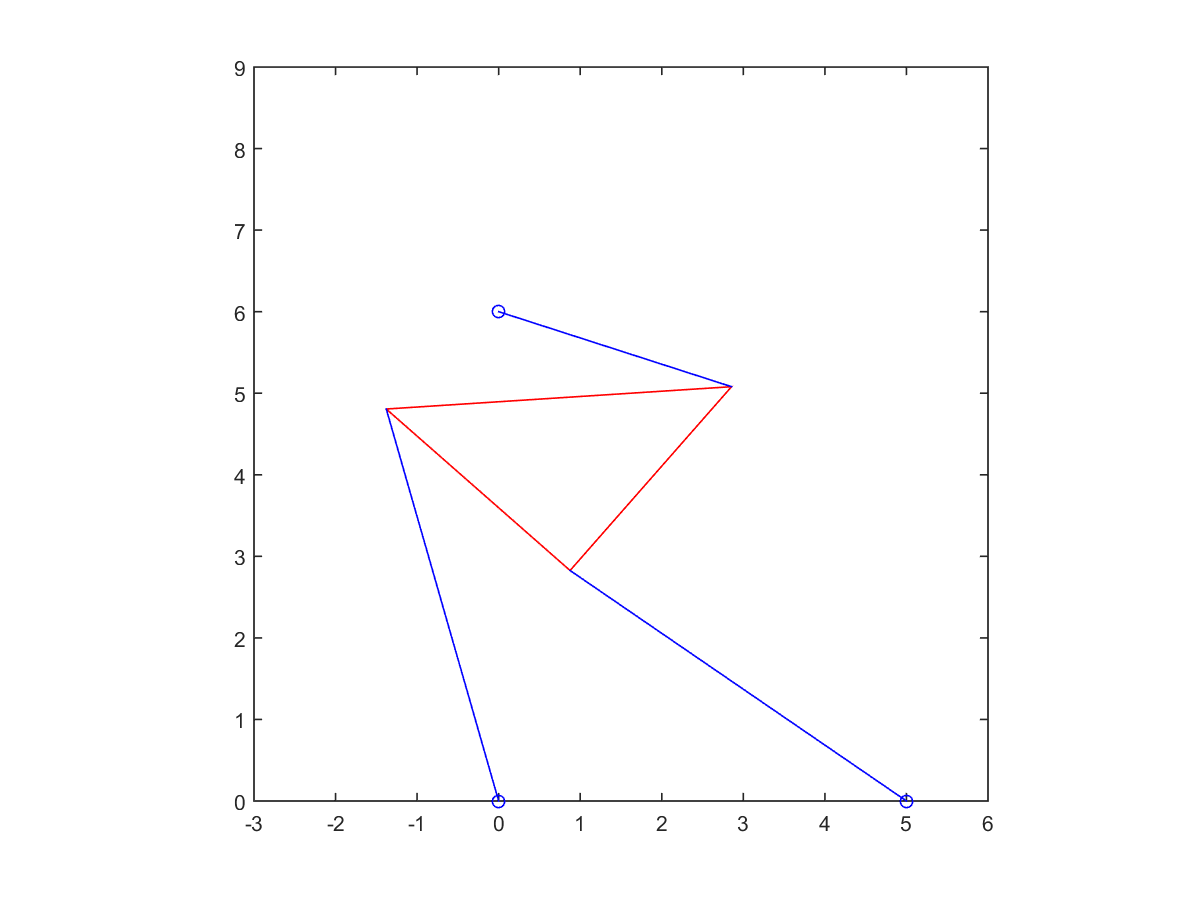
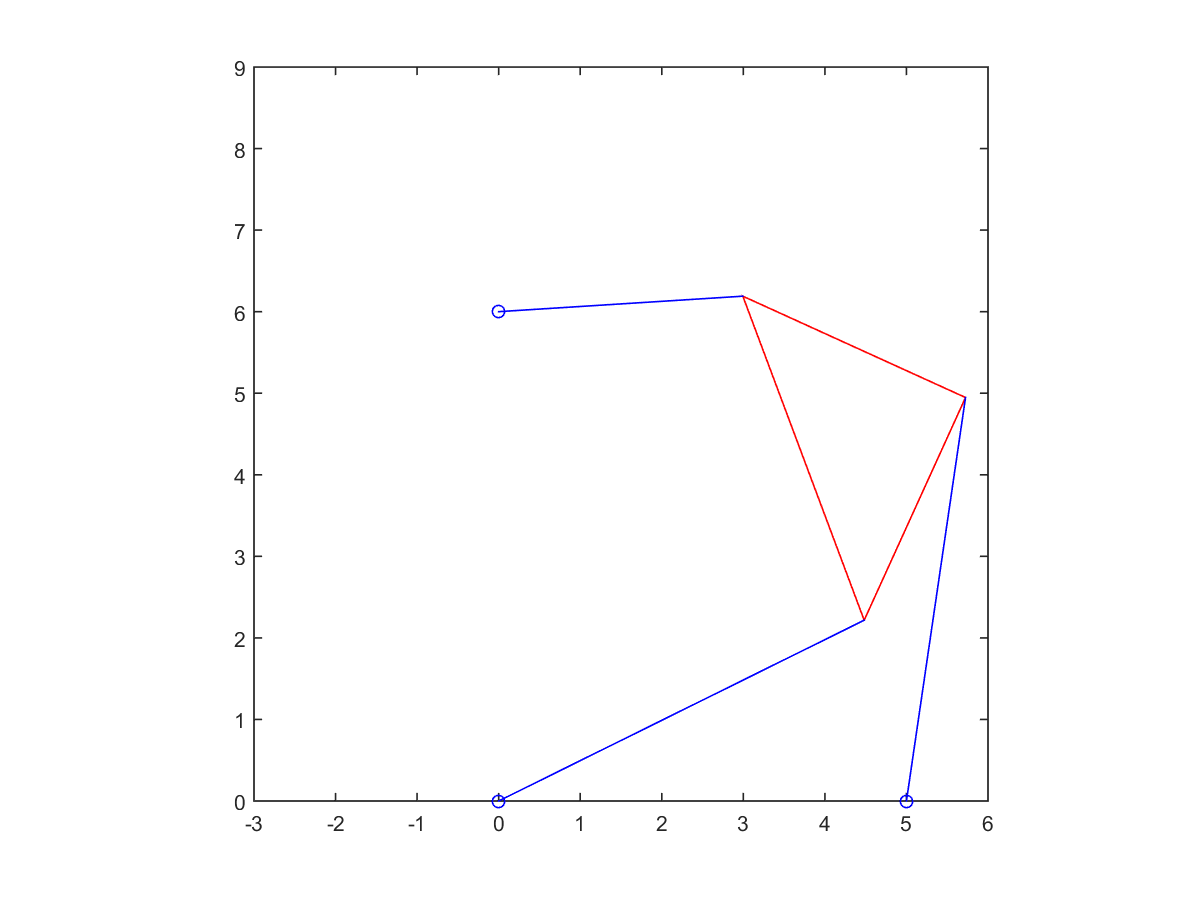
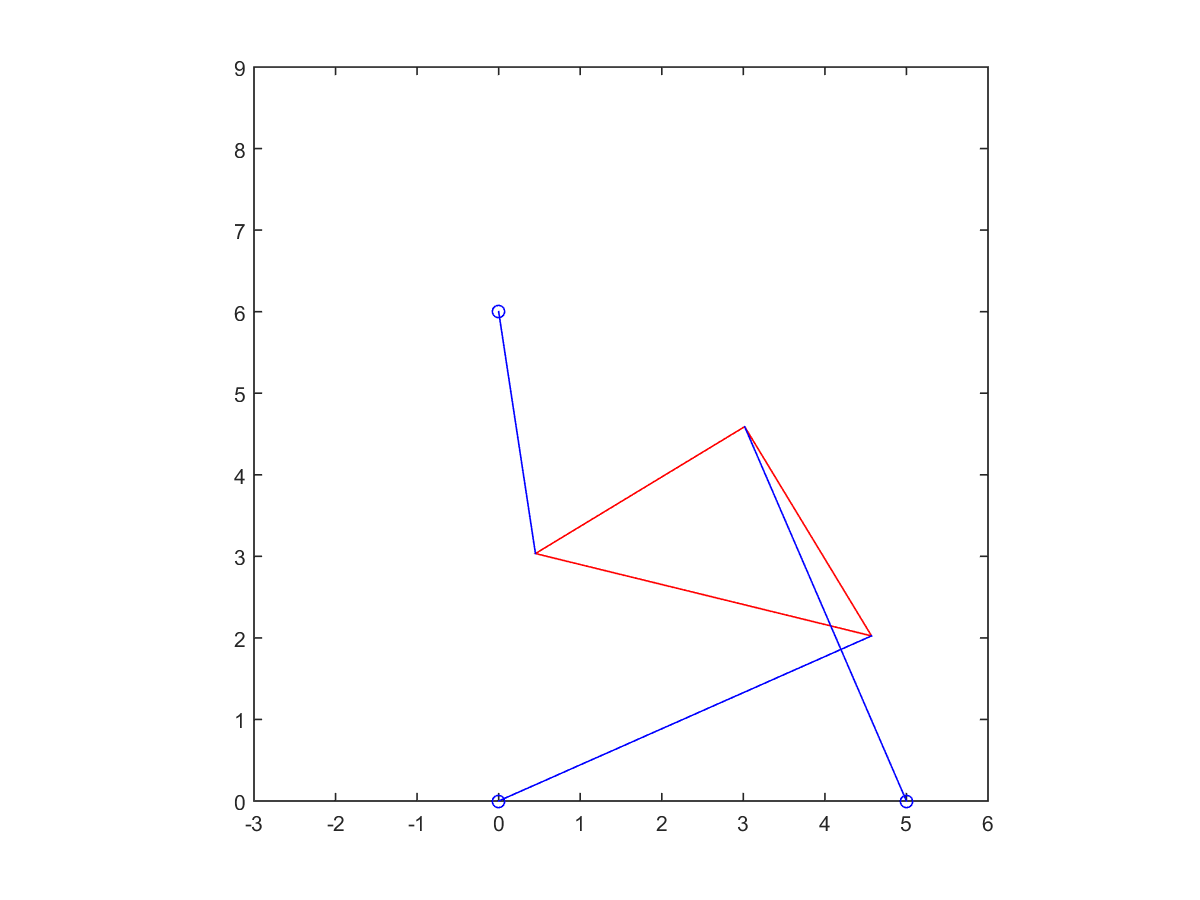
4. Solve the forward kinematics problem for the planar Stewart platform specified by \[x_1 = 5, (x_2, y_2) = (0,6),L_1 = L_3 = 3,L_2 = 3\sqrt 2,\gamma = \frac{\pi}{4},p_1 = p_2 = 5,p_3 = 3.\] Begin by plotting \(f(\theta)\). Use an equation solver to find all four poses, and plot them.
 |
 |
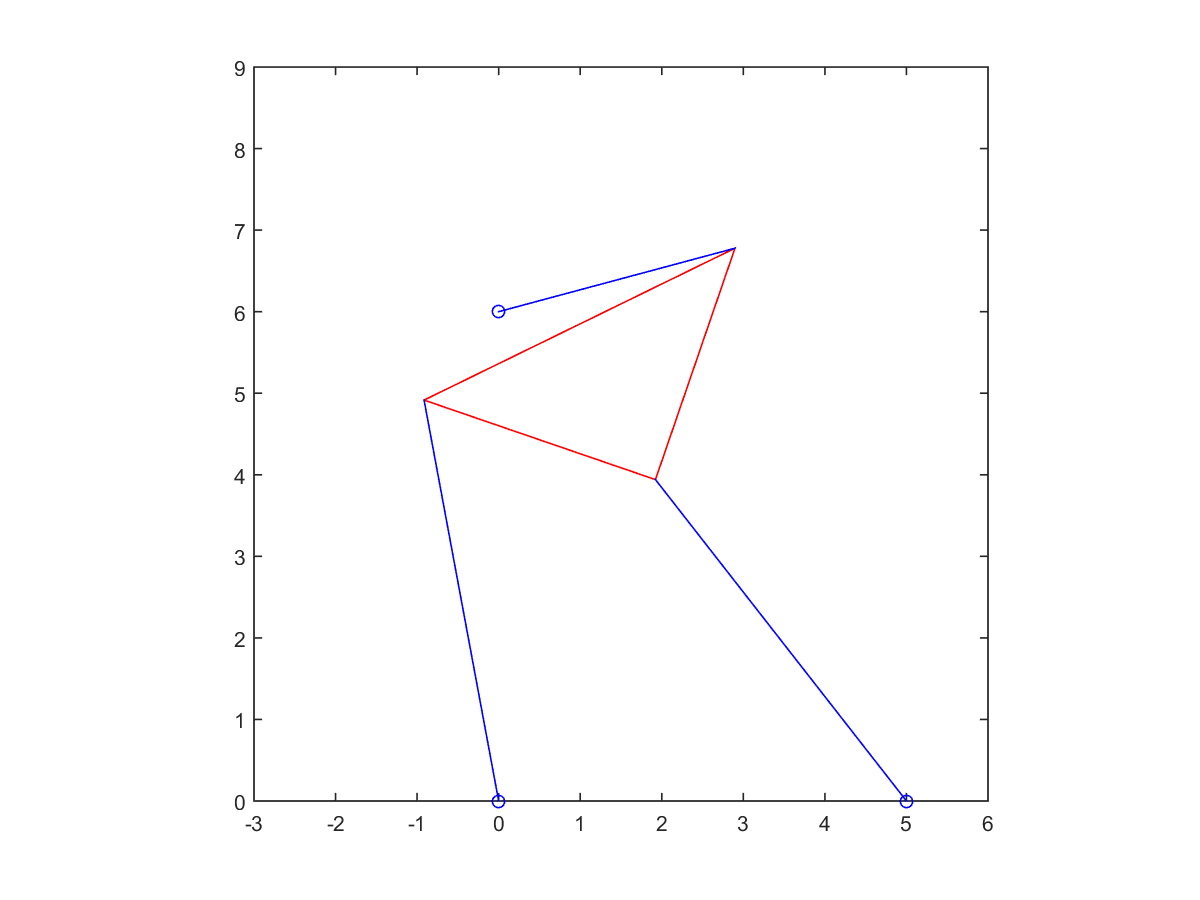 |
| Root at -0.7208 | Root at -0.3310 | |
| 
| |
| Root at 1.1437 | Root at 2.1159 |
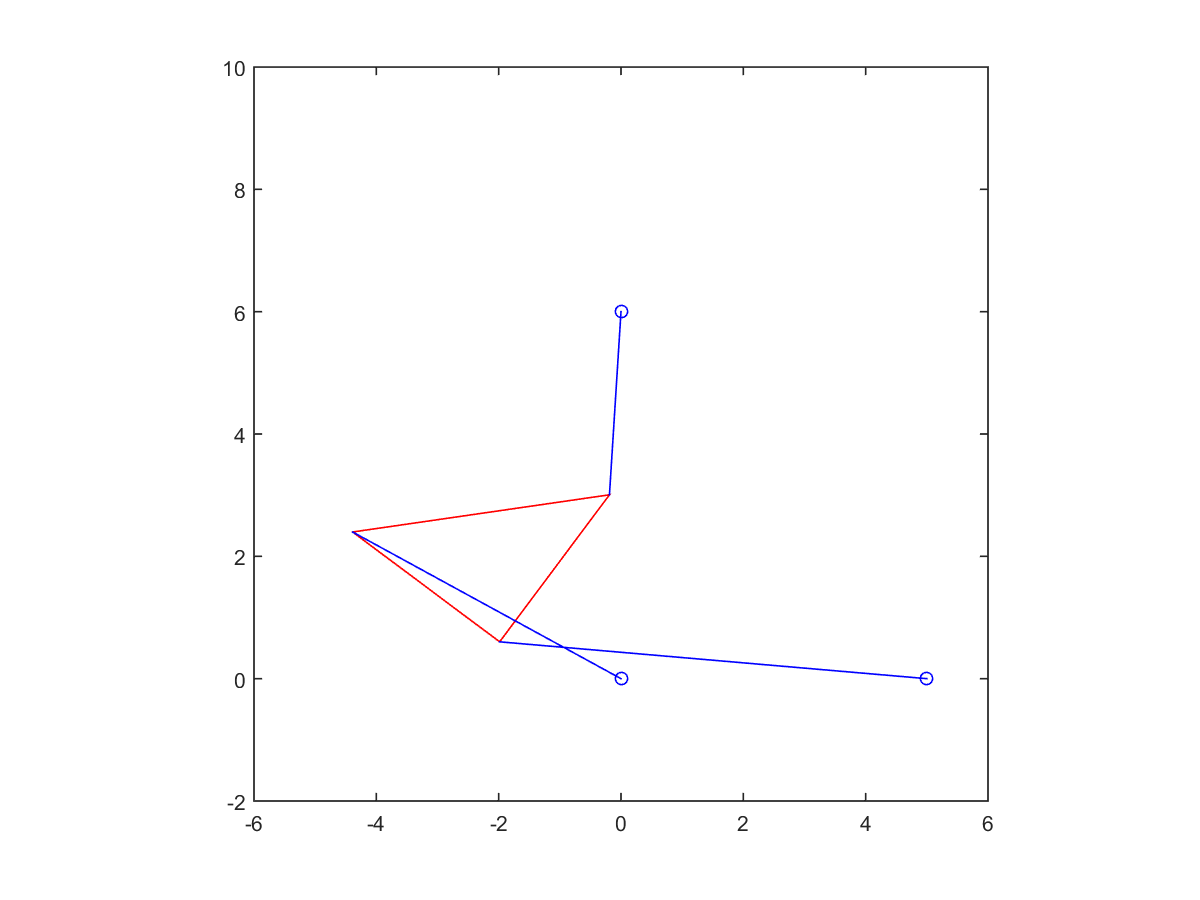
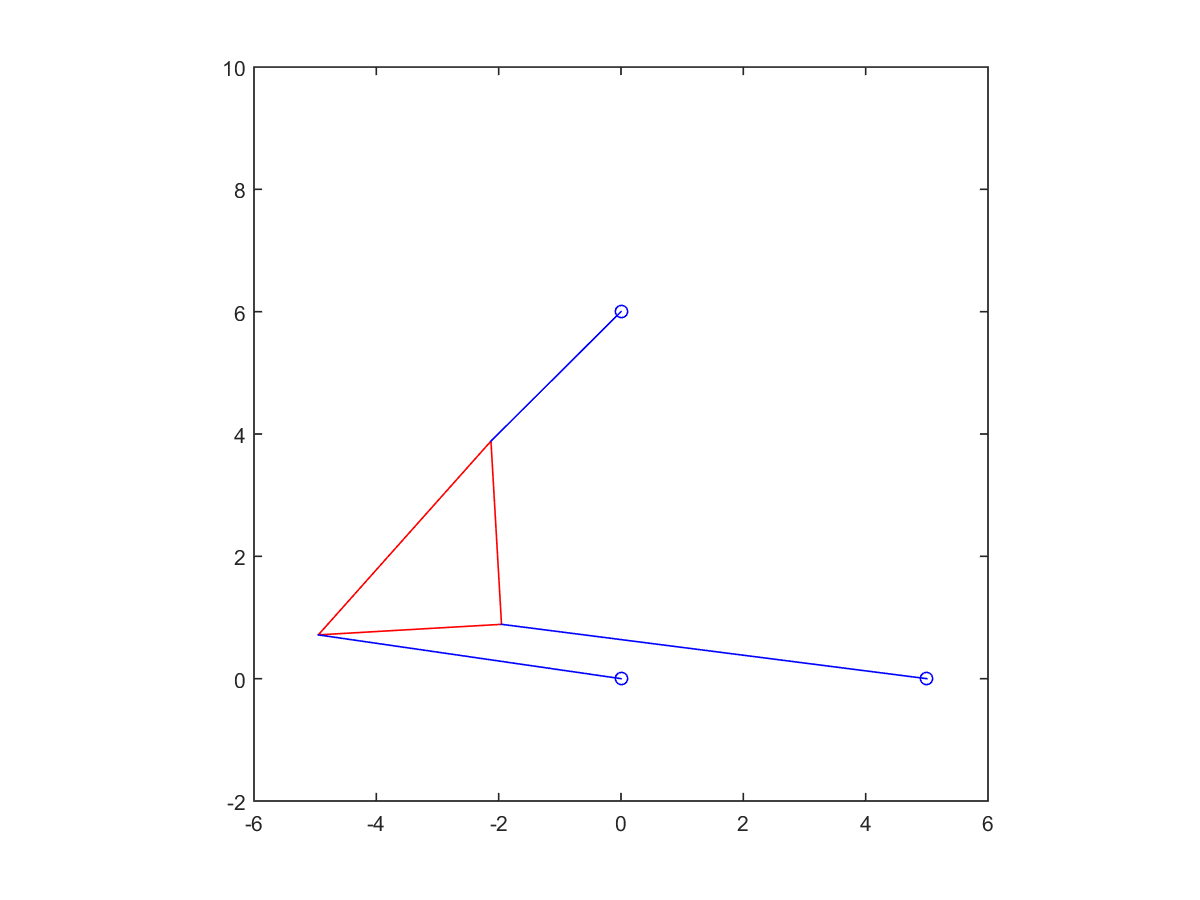
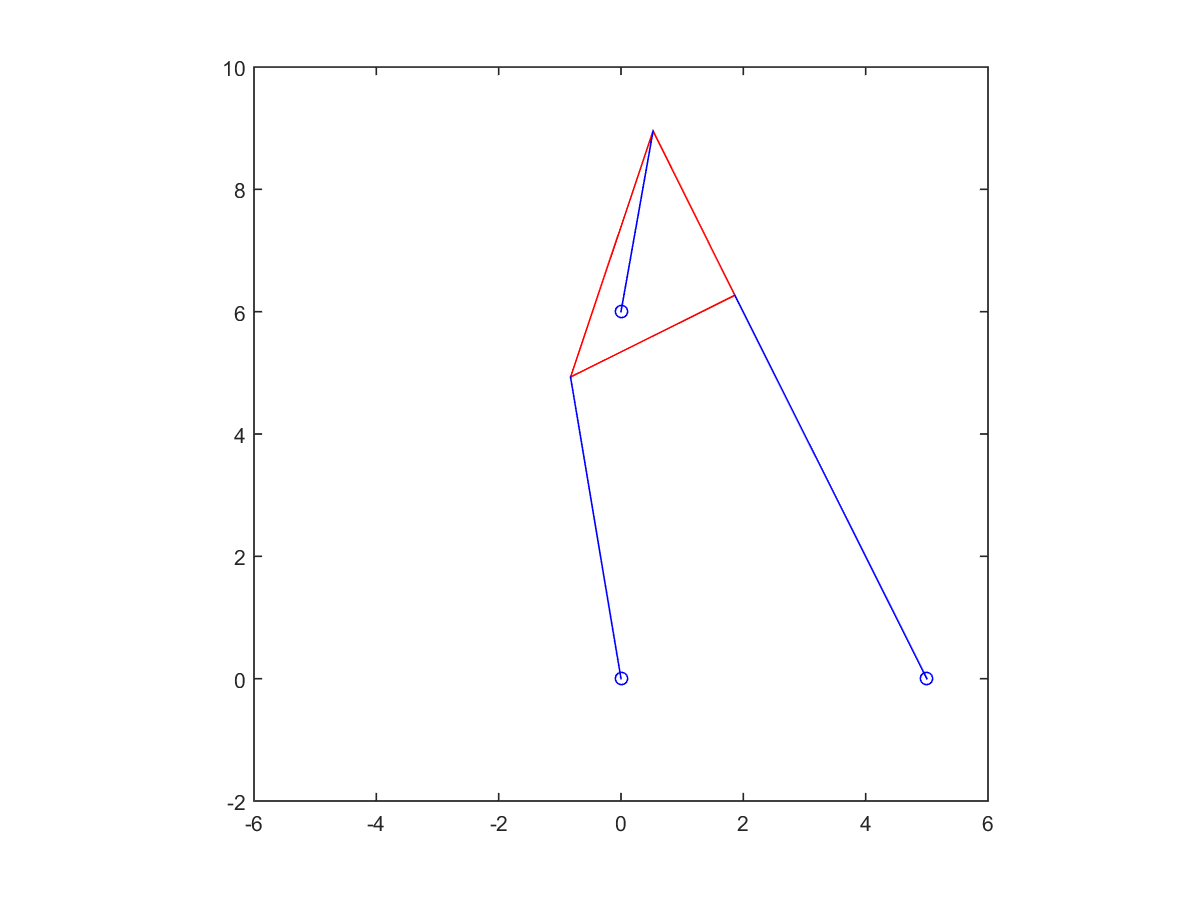
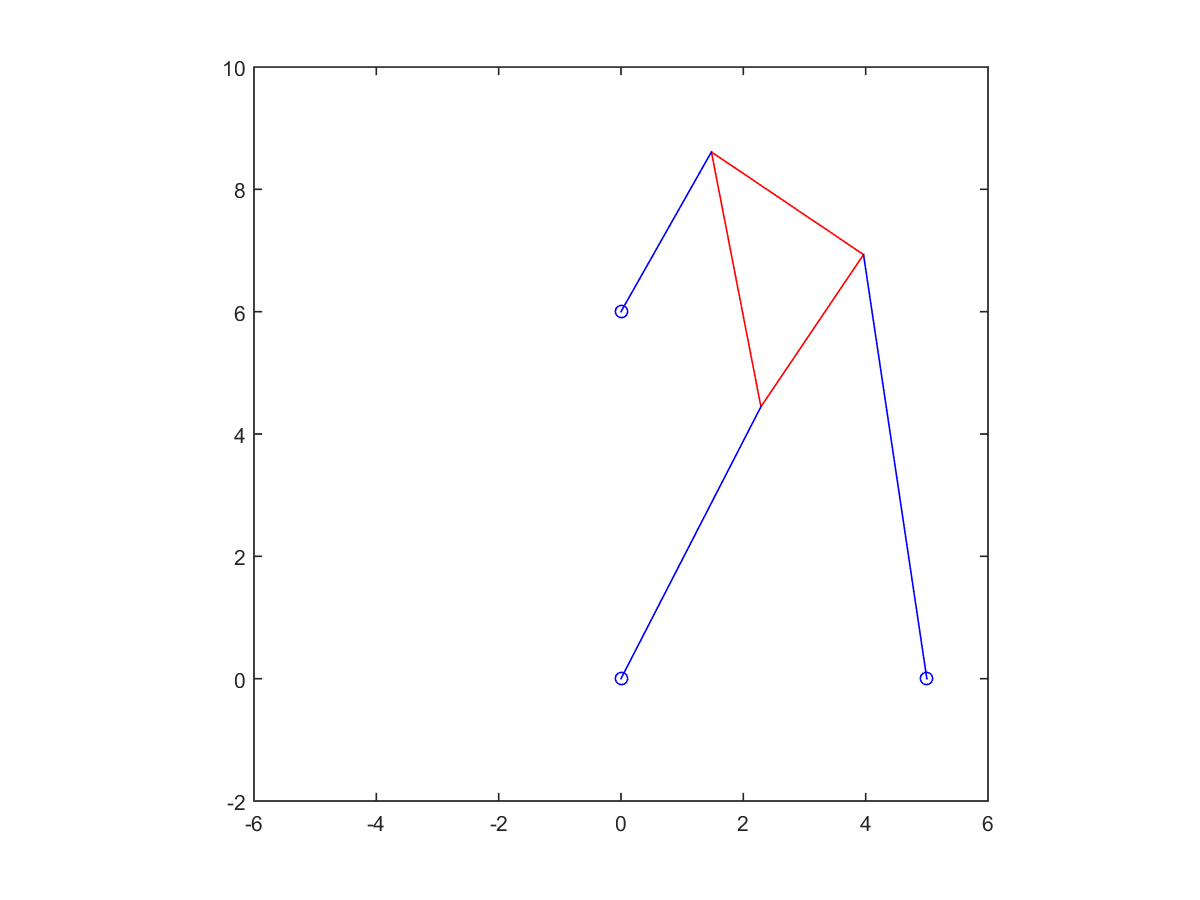
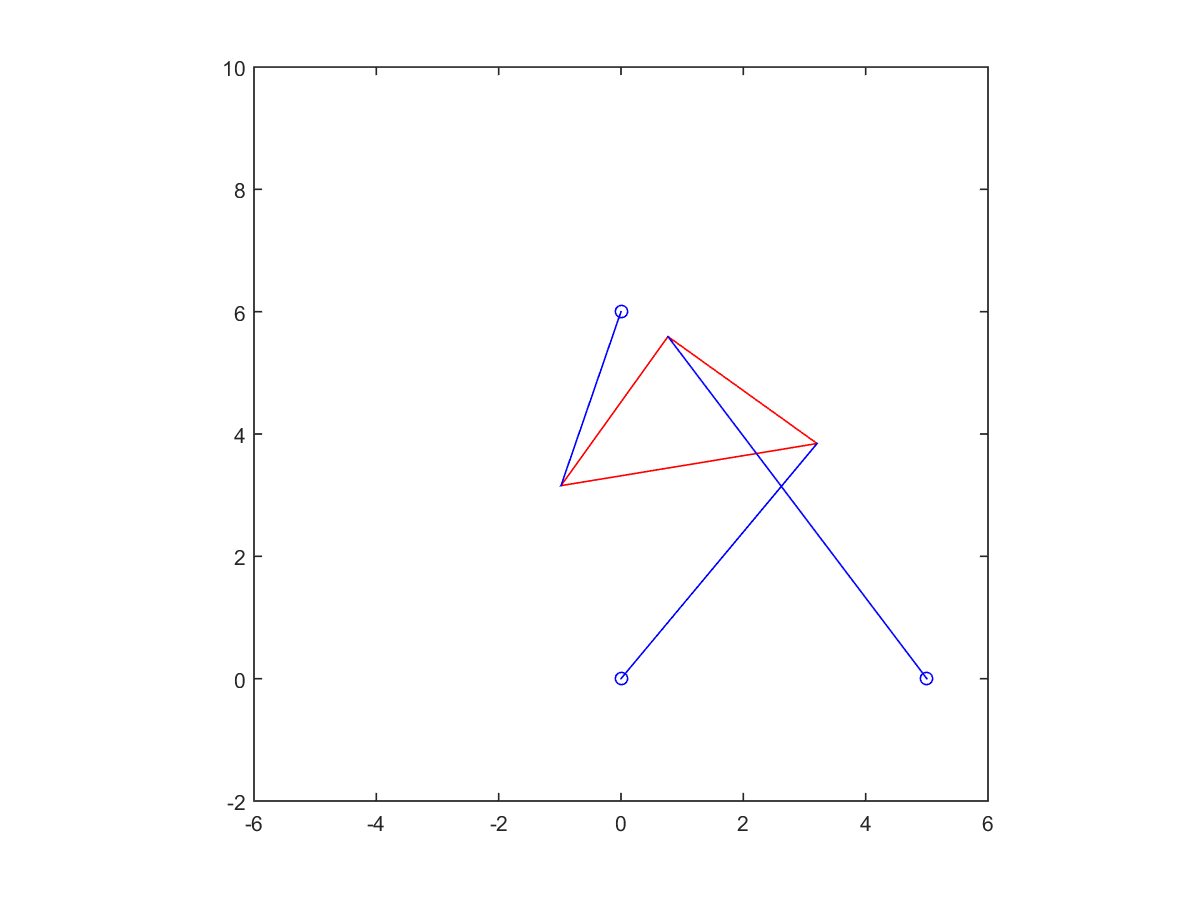
5. Change strut length to \(p_2 = 7\) and re-solve the problem. For these parameters, there are six poses.
\(p_2 = 7.01\)
 |
 |
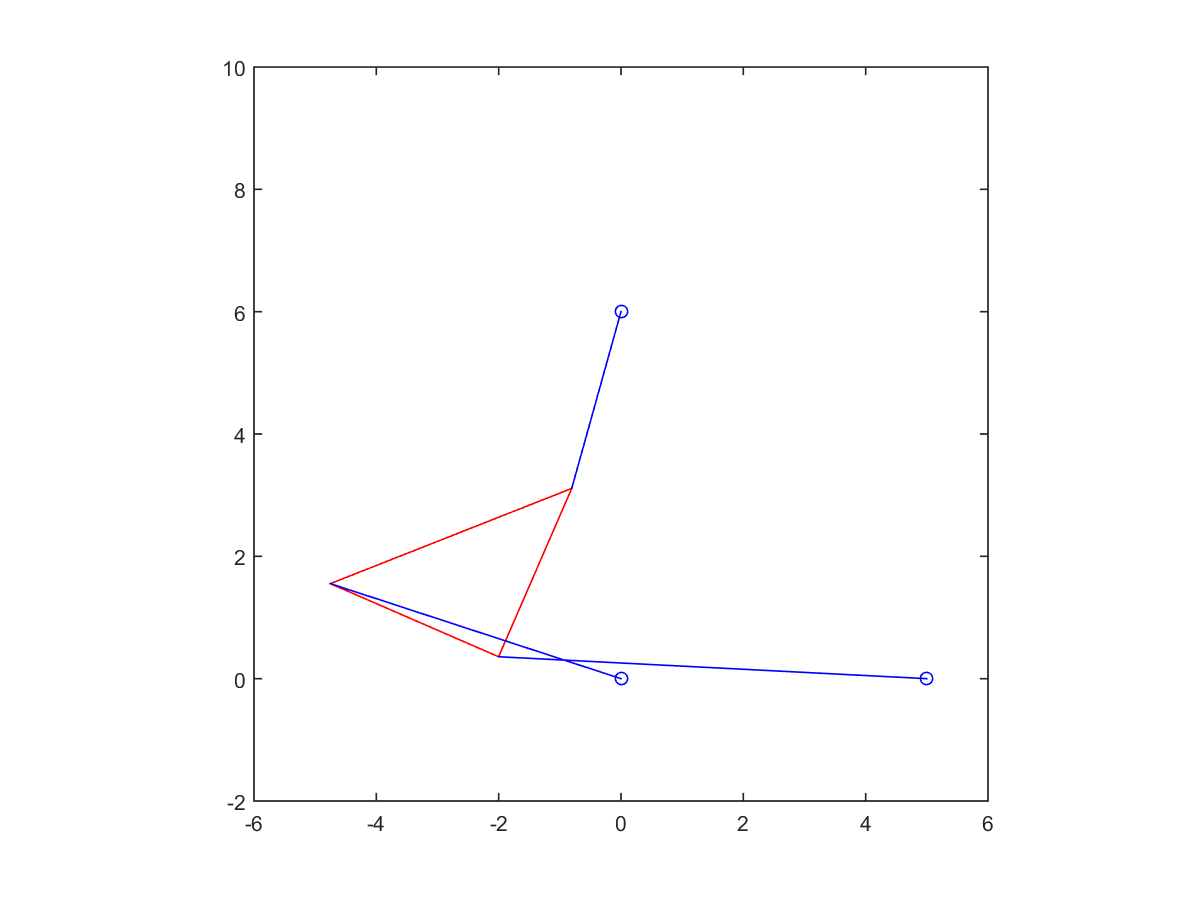 |
| Root at -0.64155 | Root at -0.40980 | |
 |
 |
|
| Root at 0.05758 | Root at 0.46170 | |
 |
 |
|
| Root at 0.97741 | Root at 2.51925 |
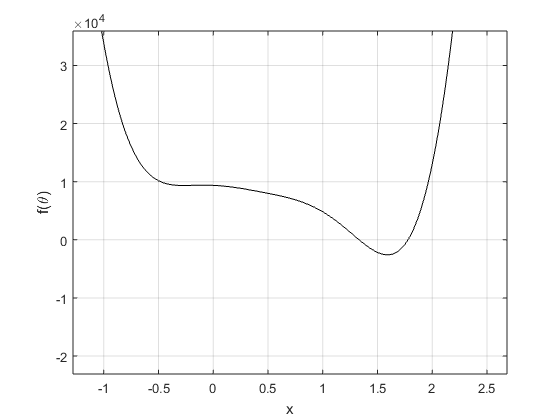
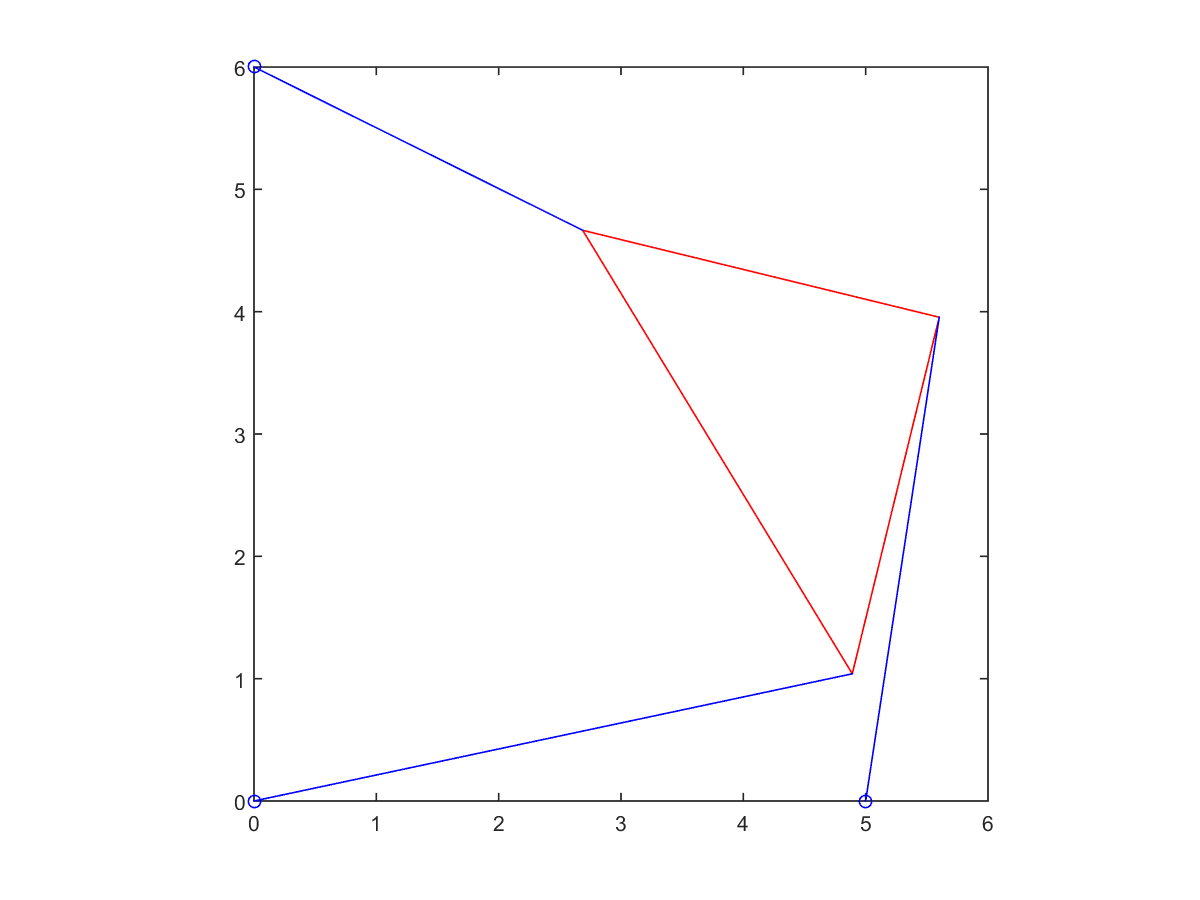
6. Find a strut length \(p_2\), with the rest of the parameters as in Step 4, for which there are only two poses.
\(p_2 = 4\)
 |
 |
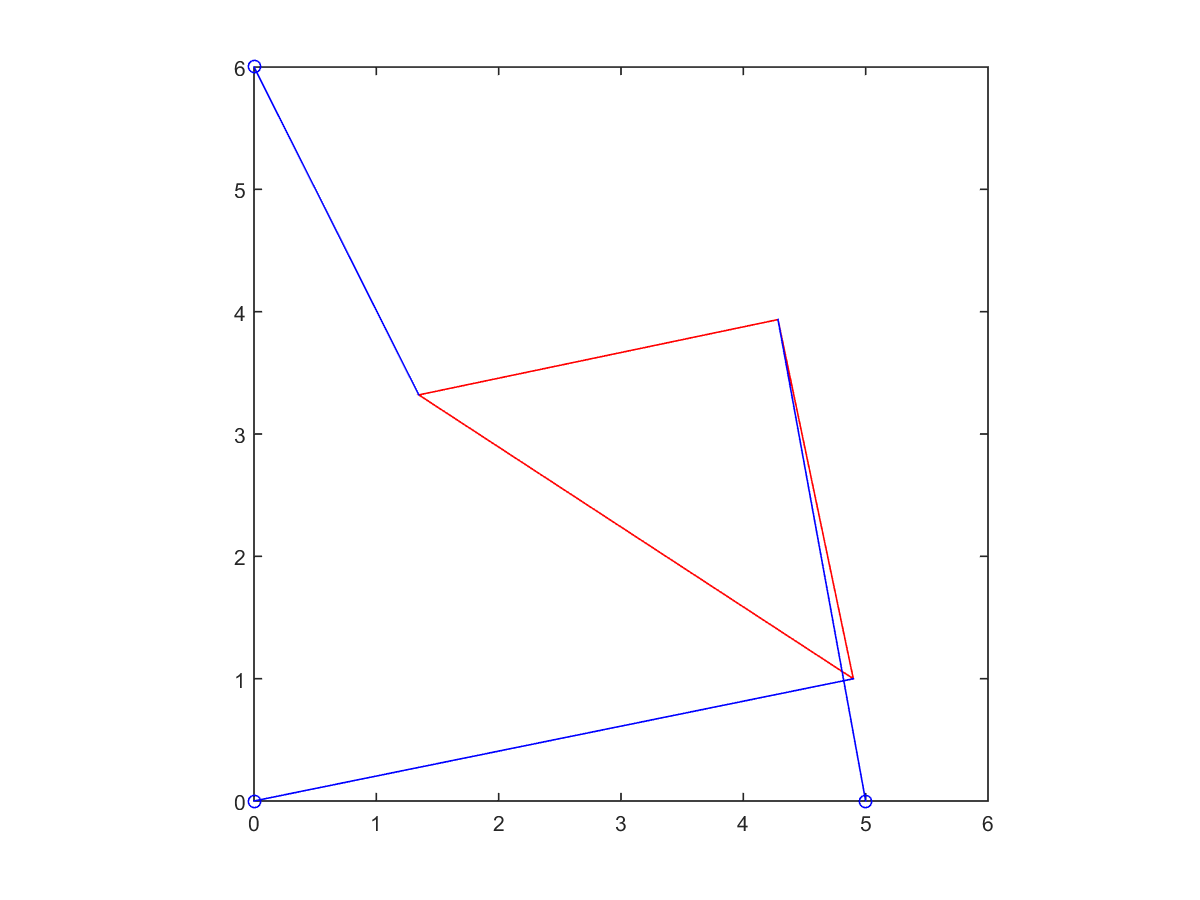 |
| Root at 1.33164 | Root at 1.77751 |