Dr. Riki Morikawa, George Mason University
update 26May2015
Signal Representation
Back to index
Sounds that we perceive through our ears, such as speech, is in the form of acoustic or mechanical waves that spread from a source in a longitudinal manner. This type of sound wave is similar to the ripples of a wave that emanate at the surface of a pond after a stone has been thrown into it (i.e., longitudinal waves are ones in which the oscillations are parallel in the direction of wave propagation or travel). Although similar to mechanical waves, electromechanical (EM) waves that are used in electronic telecommunications systems are said to be transverse vice longitudinal (i.e., traverse waves consist of oscillations that are perpendicular to the direction of wave propagation). As such, wave propagation mechanisms differ. For human speech to be transmitted via electrical wires or radio transmitters, the mechanical or acoustic waves must be converted into electrical signals. As these electrical signals travel through wired medium or antenna, EM waves are produced and emitted.
By using a transducer (i.e., a device that converts one form of energy to another) such as a microphone, we can convert mechanical speech into electrical signals. The electrical current produced by the microphone varies proportionally with speech waves entering the microphone, and is said to be “modulated” by speech. The modulated electrical current that travels through the wire also produces an EM wave or field, which is proportional to the modulated electrical signal. It is this EM field that enables radio frequency (RF) transmission from transmitter to receiver via unguided medium (e.g., air).
We can represent an electrical signal or EM wave using the sine wave formula, x(t)=A sin(2pft ± theta ), fig. 1, where
A, amplitude, or strength, of the signal (e.g., typically voltage or power)
f, frequency of the signal in cycle per second (Hertz)
t, time in seconds
theta, phase angle of the signal which represents the angle (typically in degrees or radians) of the start of the wave from a reference point (t=0 seconds). Note: π radians = 180 degrees

Figure 1. Sinusoidal Wave
Figure 1 shows the sine wave, or signal, represented in the time domain where the x-axis represents time in seconds, and the y-axis is amplitude (e.g., power, voltage, etc.). In this figure, we selected a sine wave, however, we could have easily selected a cosine wave to represent our waveform. The difference between a sine wave and cosine wave is that they are 90 degrees, or π/2 radians, apart. Figure 2a shows a sine wave, and figure 2b shows the cosine wave. By inspecting the two waves, we see that the cosine wave has "peaked" one quarter of a wave before the sine wave. As such, we say that the cosine wave "leads" the sine wave by 90 degrees. x(t)=A sin(2pft)= A cos(2pft + π/2 radians)
Figure 2. a. Sine Wave, b. Cosine Wave
Example 1: From the following formula, determine the amplitude (signal strength), frequency, and phase angle.
x(t)= 25 sin(1000pt + 90o )
Answer 1: A = 25, theta= 1.57 rads = π/2 rads = 90o , note: π=180 degrees
Thus far we have looked at a signal and how the amplitude of the signal varies with time (i.e., time domain). However, equally important in communications is understanding how the signal varies with frequency (i.e., frequency domain). There is an inverse relationship between frequency and the time period of a sinusoidal wave: frequency=1/T, where T is the period of the wave in seconds (i.e., the time in seconds that it takes for a wave to complete one full cycle).
Let's discuss the difference between “frequency” and “frequency bandwidth”. For telephone service, the frequency range that is needed to transmit voice grade electrical signals is 300Hz to 3400Hz. Therefore, the frequency “bandwidth” required to send a voice grade signal through telephone wires is:
fBW = fH – fL = 3400 – 300Hz = 3100 Hz (frequency bandwidth)
Now that we have an electrical voice signal with a frequency bandwidth of 3100 Hz, we can modulate this signal onto a carrier frequency wave. As an example, if you tune your radio to 88.5MHz, you're actually tuning your radio to the carrier frequency itself. Note: Modulation techniques are covered in another tech note.
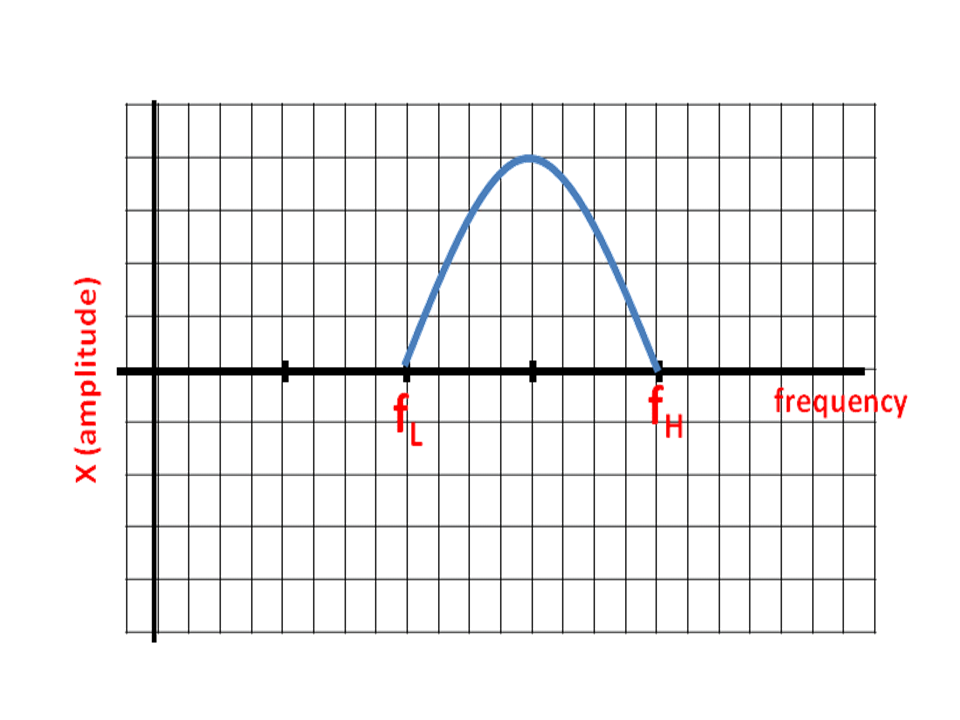
Figure 2. Frequency Bandwidth shown in the frequency domain
In comparison, human hearing is more sensitive. The frequency bandwidth associated with CD quality music is between 20Hz and 20,000Hz (or 20kHz). So if we were to design a communications system to send high quality music, we would not use a normal voice grade quality circuit with a bandwidth of 3100Hz, but would rather require a transmission system that could support a frequency bandwidth of approximately 20kHz or greater.
Note that “bandwidth” is also referred to as “capacity” which is measured in bits per second (bps) vice Hertz. Capacity and frequency bandwidth are closely related, and we will see in later lessons how equations such as Shannon-Hartley and Hartley’s formula for capacity and bandwidth are used to determine this relationship.