Eb/No and Data Rate
Back to Index
Determining Data Rate Using Eb/No
When we establish a wireless link, our goal is to ensure that sufficient power reaches the receiver. The amount of received power will depend upon the design of the receiver itself. Receiver sensitivity gives you the lowest receive power that a particular receiver requires to successfully detect the signal and demodulate the data. As we know, thermal noise is always present and can dramatically impact our ability to detect a signal. Therefore, it is important that the signal-to-noise ratio (SNR or S/N) be sufficiently large enough to enable receiver detection and demodulation (i.e., meet minimum receiver sensitivity).
When we consider RF communications, we use carrier signals to transmit our data. The data is modulated onto a carrier wave using methods such as Phase Shift Keying (PSK), Frequency Shift Keying (FSK) or Amplitude Shift Keying (ASK). The receiver detects the carrier wave as well as the noise. Therefore we are concerned with the amount of carrier power to noise ratio (C/N) that reaches our receiver. We will use C/N vice SNR for the remainder of this note.
Let's revisit the link equation in decibel form:
[Pr] = [Pt] +[Gt] + [Gr] - [FSL], in decibels!
Pr=receive power, Pt=transmit power, Gt=transmit antenna gain,
Gr=receive antenna gain, FSL=free space loss
In the above equation, we are concerned with the amount of power that finally reaches our receiver behind the receive antenna. The received power, Pr, is the power of the carrier signal received (C), or Pr=C. We also know that there will be thermal noise associated with our carrier signal.
C/No = Pr/kT
No=Noise density (noise power in 1Hz), k=Boltzmann's constant-1.38E-23 J/K, T=temperature in Kelvin
As an example, say that you performed your link calculation and determined that the carrier power received will be C=-41dBm. You also determine that the noise density of your system is No=-96dBm. Therefore, in decibels, [C/No]= -41 - [-96] = +55dBm.
Now that you know what your C/No is, and provided your receiver's sensitivity is low enough to detect the signal, you can then calculate an achievable data rate based upon the bit error rate (BER) you desire. This is where energy bit per noise density (Eb/No) comes in.
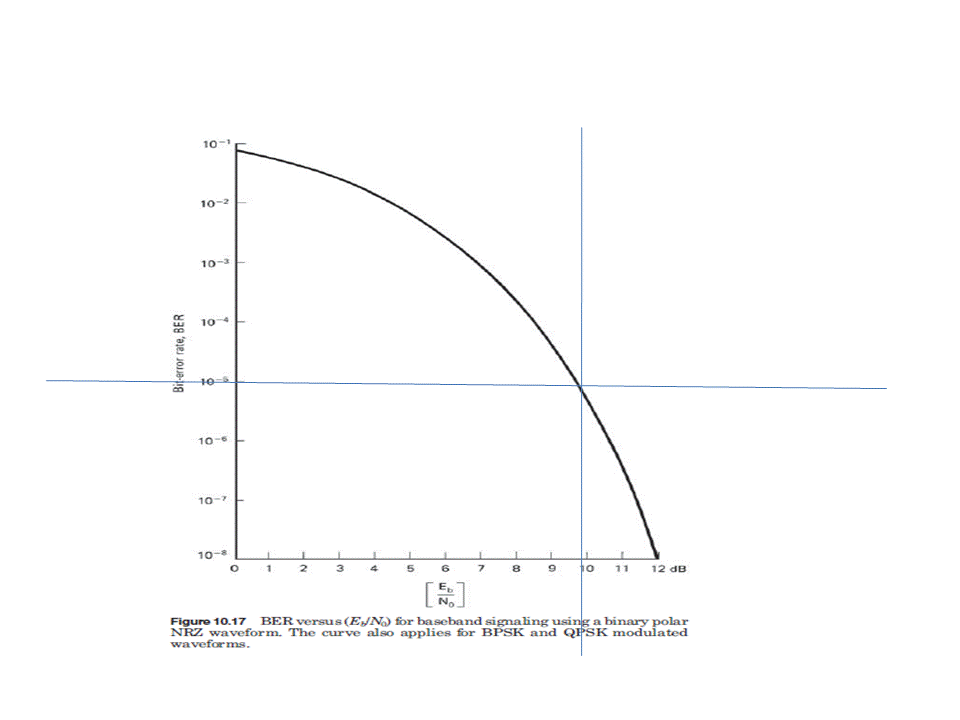
The figure below shows a plot of BER versus Eb/No, The curve in the graph is specific to the type of RF modulation method used. Let's say that you need to have a BER of at least 1E-5 (or 1 bit error out of 100,000 bits) in order to establish a reliable telecommunications link. Following the curve, you find that you will need an Eb/No of approximately 10dB.
The following equation is used to determine the data rate possible given C/No and Eb/No:
[C/No] = [Eb/No] + [R], in decibels
R=data rate
Continuing with our example:
[C/No] = [Eb/No] + [R]
+55dBm = 10dB +[R]
[R] = +55dBm - 10dB = 45dB
R = 10(45/10) = 31.6E3 bps = 31.6 kbps
Therefore, in our example, we find that we can establish a data rate of approximately 31 kbps with a BER=1E-5 over our link.
Eb/No is essentially the energy stored within a single bit. We know that power equals energy over time, so there is a direct and proportional relationship between bit energy and receive signal power. By selecting a modulation method and desired BER you can determine the achievable data rates. For data communications, Eb/No plays a critical role in system design.
Note: Diagram from "Satellite Communications", Dennis Roddy, 4th ed., McGraw-Hill, NY, 2006.