Project 1
Kinematics of the Stewart Platform
Kathleen McLane, Tim Reid, and Paul McNulty
A Stewart platform is a platform that is held up by arms which have variable lenght. The
position of the platform is controlled by the length of the arms. For each length of
the arms, there exists multiple positions the platform can be in. The different positions
of the platform are denoted by the angle the platform takes in relation to the horizontal
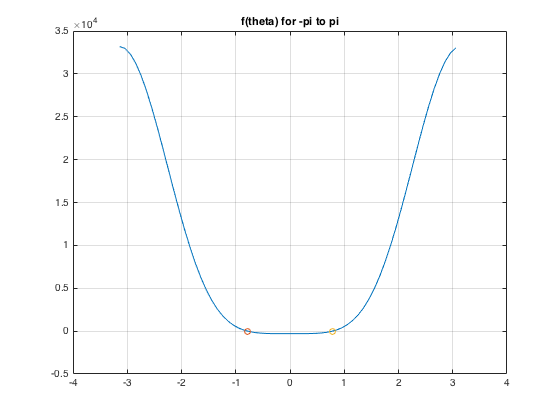
axis. We denote this angle by \(\theta\). The values of \(\theta\) for the specified
parameters are the zeros of the function \[f(\theta )=N_1^2+N_2^2-p_1^2D^2 \] where
\begin{align*}
N_1 &= B_3(p_2^2-p_1^2-A_2^2-B_2^2)-B_2(p_3^2-p_1^2A_3^2-B_3^2) \\
N_2 &= -A_3(p_2^2-p_1^2-A_2^2-B_2^2)+A_2(p_3^2-p_1^2A_3^2-B_3^2) \\
D &= 2(A_2B_3-B_2A_3) \\
A_2 &= L_3\cos \theta -x_1 \\
B_2 &= L_3 \sin \theta \\
A_3 &= L_2 \cos (\theta +\gamma )-x_2 \\
B_3 &= L_2 \sin (\theta +\gamma )-y_2 \\
x &= \frac{N_1}{D} \\
y &= \frac{N_2}{D}.
\end{align*}
The values \(L_1,L_2,L_3,x_1,x_2,y_2, \text{ and } \gamma \) are parameters that are
fixed by the setup of the Stewart platform. The values \(p_1,p_2,p_3 \) are the lengths
of the legs of the Stewart platform.
We built a function for \(f(\theta)\) and tested it
at the recommended values to make sure it was working well. The code for \(f(\theta)\) can be
found here: f.m
In order to find the zeros of \(f(\theta)\), corresponding to the theta values for each postion
the platform could take, we chose to use the bisection method. In order to do this, we
needed a way to pass theta values into the bisection method given the values for gamma,
the strut lengths, the strut anchors, and the triangle side lengths. So we built functions
that would calculate the value of theta such that \(f(\theta)\), and then used an analogous
code to calculate x and y for the first vertex of the triangle. The formulas found in
these codes were given in equations (1.39) and (1.40) in the book. These three scripts can
be viewed here: P1Bisect.m,
Project1FInputs.m,
and Project1xy.m.
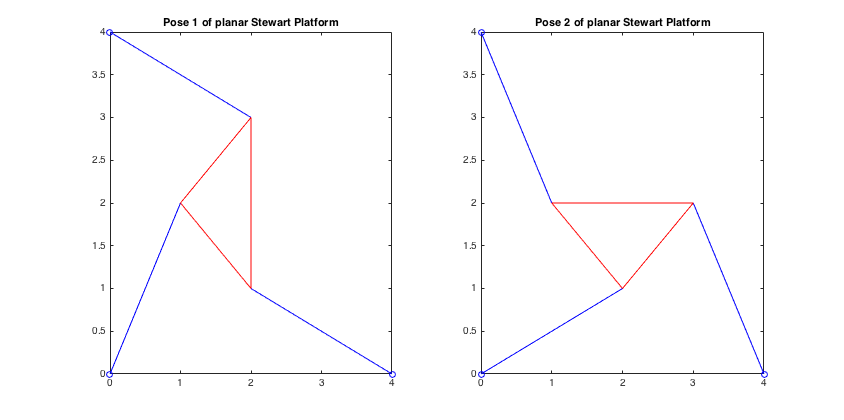
Finally, we needed a script to give the other two vertices of the triangle given x, y, and
theta, as well as a way to reliably check the strut length. It was noticed that equation
(1.38) in the book that gives the strut length seems to cause some kind of circular
referencing, so instead we calculated the strut lengths directly from the plotted vertex
values. The vertex locations and strut lengths were calculated using this script:
vertices.m
These scripts were written in order to complete parts 4, 5, and 6 of the problem, and the
details of each part can be found here:
Part 4,
Part 5, and
Part 6.
Also worth noting, parts 2 and 3 asked for some plotting in order to verify our scripts
were working properly, so those plots can be seen here: