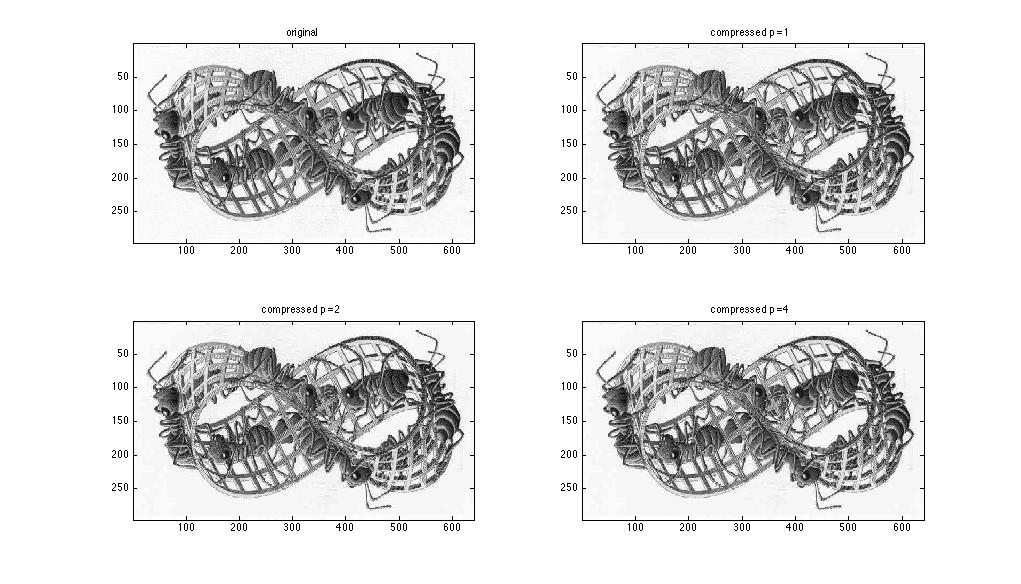
Starting with a gray image, we were ask to first explore compression on an 8x8 section of our matrix, and then use that 8x8 compression method to rebuild the image.
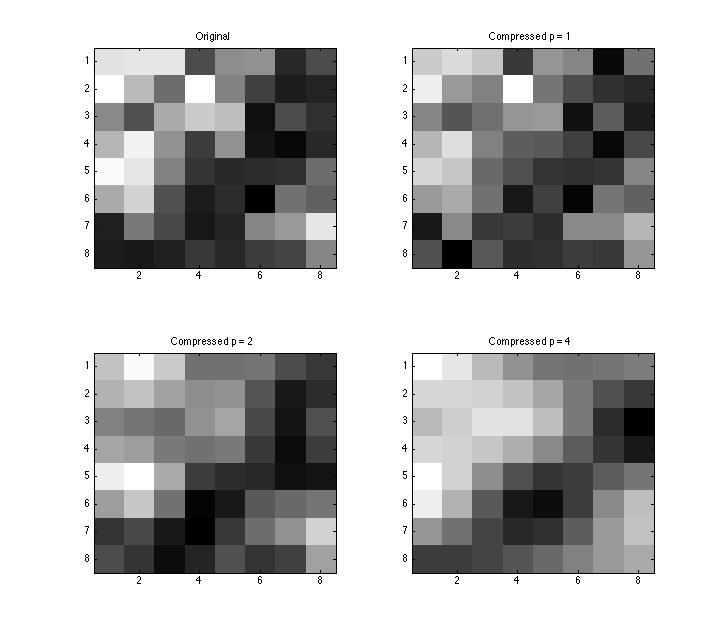
So, starting with the Escher B&W image, I selected out an 8x8 square and ran through the linear quantization with loss parameters p = 1, 2, and 4.
Using this 8x8 image, I took the linear quantization matrix with the loss parameter p: \[Q=p\begin{bmatrix} 8 & 16 & 24 & 32 & 40 & 48 & 56 & 64 \\ 16 & 24 & 32 & 40 & 48 & 56 & 64 & 72 \\ 24 & 32 & 40 & 48 & 56 & 64 & 72 & 80 \\ 32 & 40 & 48 & 56 & 64 & 72 & 80 & 88 \\ 40 & 48 & 56 & 64 & 72 & 80 & 88 & 96 \\ 48 & 56 & 64 & 72 & 80 & 88 & 96 & 104 \\ 56 & 64 & 72 & 80 & 88 & 96 & 104 & 112 \\ 64 & 72 & 80 & 88 & 96 & 104 & 112 & 120 \end{bmatrix}\]
I compressed the 8x8 block using the code gry8.m, and the resulting linearly quantized matrices \(Y_Q\) can be seen below.
For \(p=1,\ \) \(Y_Q=\begin{bmatrix} -12 & 12 & 4 & -1 & 1 & -1 & 0 & 0 \\ 8 & 8 & -3 & 1 & 1 & 0 & 0 & 0 \\ 0 & -3 & -1 & 0 & 0 & 0 & 1 & 0 \\ 2 & 1 & 2 & 0 & -1 & -1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & -1 & 1 & 0 \\ 0 & -1 & 0 & 0 & -1 & -1 & 0 & 0 \\ -1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}\)
For \(p=2,\ \) \(Y_Q=\begin{bmatrix} -6 & 6 & 2 & 0 & 0 & -1 & 0 & 0 \\ 4 & 4 & -2 & 0 & 0 & 0 & 0 & 0 \\ 0 & -2 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & -1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}\)
For \(p=4,\ \) \(Y_Q=\begin{bmatrix} -3 & 3 & 1 & 0 & 0 & 0 & 0 & 0 \\ 2 & 2 & -1 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}\)
Then, I reconstructed the image using dequantization, and the images can be seen below.