ALGEBRA, FUNCTIONS, AND DATA ANALYSIS – COURSE 2

PRE-TEST/POST-TEST

Name______________________________

Date_______________________________

Answer each question below as completely as possible. Show all applicable work. When noted, justify your answers. Completion of the test will be limited to 1 ˝ hours.

 

1.       20 students took a test graded out of 60 points.  The set of scores is shown below.

{7, 13, 19, 21, 24, 25, 26, 26, 32, 33, 35, 35, 35, 40, 44, 47, 57, 57, 59, 60}

A.  Determine the following:

Mean   ____34.75_______                 Quartile 1 _____24.5_____   Interquartile Range __21____  

Median  ____34___________            Quartile 2_____34_______  Minimum______7_______

Mode   _____35__________              Quartile 3_____45.5_______  Maximum____60_______

Range ____53___________             

 

B.  Create a box-n-whisker using applicable data from above.  Label.

           Min =7                                                                               Max = 60

 

      0   4   8   12   16   20   24   28   32   36   40   44   48   52   56   60   64 

                                         Q1 24.5   Q2 34           Q3 45.5

2.      What is the sum of the differences between the given value and the mean?  Why?

   0 Because the mean is a balance point between all the data.

 

 

 

 

3.      A set of data is normally distributed with mean 30 and standard deviation 8.

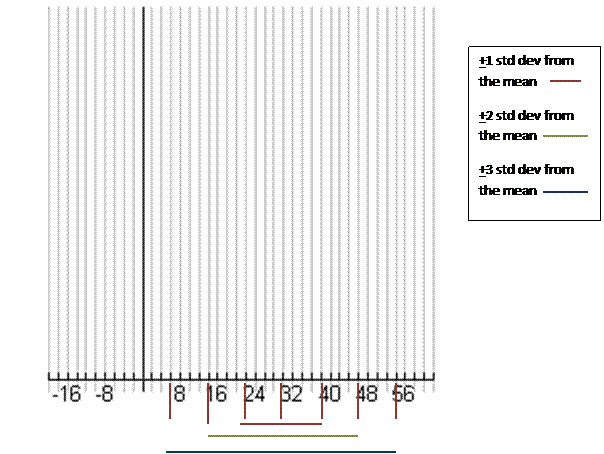A.  Draw the normal curve that will model this data on the coordinate plane below. 

 

 

 

 

 

 

 

 

 

 

 

 

 

B. Approximately what percent of the observations are between the mean and 1 standard deviation to the left of the mean? 

1 standard deviation from the mean, left and right, is 68%. Therefore since the normal curve is symmetrical then from the mean to 1 std dev to the left is 34%.

4.      Explain in writing and pictures how changing the mean value changes the normal curve?

Translation of the normal curve. “The Bump” moves so that the high point is at the mean.

 

5.      Explain in writing and pictures how changing the value of the standard deviation changes the normal curve?

Scale change. The normal curve will become flatter and more spread out as the std dev becomes larger. The smaller the std dev the taller the “bump”.

 

6.   The mean running time for a cross country race is 150 minutes with a standard deviation of 25, explain what a z-score of -2 means?

z-score of -2 is 2 standard deviations below the mean which means 2.5% of the running times are below 100 minutes.

7.   An annual corn crop per acre for a Midwestern state in a particularly good year was normally distributed with a mean of 150 bushels per acre and a standard deviation of 22 bushels per acre.

A.  What percent of the farmers harvested between 130 and 180 bushels per acre?

ShadeNorm(130,180,150,22) = .732008         

so 73.2% of the farmers harvested between 130-180 bushels per acre.

B.  How many farmers had a yield of more than 180 bushels per acre?

ShadeNorm(180,x,150,22) = .084991         

so 8.5% of the farmers harvested more than 180 bushels per acre.

8.      According to the U.S. Department of Agriculture (www.usda.gov), in 2002, the mean corn crop yield in Ohio was 89 bushels per acre. In 2003, the mean corn crop yield in Ohio was 156 bushels per acre. Assume that the standard deviation in both years was the same at 25 bushels per acre.

             

A.    Farmer Jones had a crop yield of 95 bushels per acre in 2002. Find his z-score for that crop.

 

z-score = 95-89    =  0.24

                             25

 

B.     In 2003, Farmer Jones had a crop yield of 150 bushels per acre. Find his z-score for that crop.

 

z-score = 150-156    =  -0.24

                             25

 

C.     According to the z-scores, in which year did Farmer Jones have a better crop in comparison to his colleagues? Explain your answer.

In 2002, Farmer Jones had a better crop yield than his fellow farmers. In 2004 his z-score was actually negative, meaning that while his overall yield was higher, he actually had a lower crop yield than his fellow farmers.

 

 

9.      The school band sells chocolate bars each year as a fundraiser. The table below shows the number of candy bars that students in the clarinet section sold.

63

74

102

63

42

96

73

68

88

82

61

79

84

67

56

49

63

94

A.  Complete the following frequency table.

Number of Candy Bars Sold

Frequency

40-49

2

50-59

1

60-69

6

70-79

3

80-89

3

90-99

2

100-109

1

 

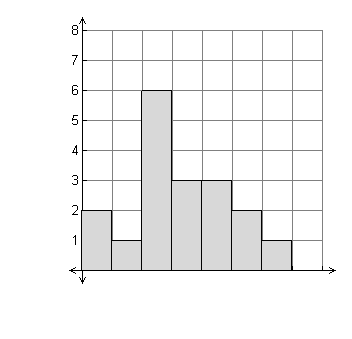Text Box: Number of Students Sold Within the RangeText Box: 40-49Text Box: 50-59Text Box: 60-69Text Box: 70-79Text Box: 80-89Text Box: 90-99Text Box: 100-109B.  Use your frequency table to create a histogram of the data.  Be sure to label axis.

 

 

 

 

 

 

 

 

 

10.  The following survey has some form of bias.

             

            Dr. Aleman wants to survey her patients to determine what kind of foods they like so that she may better understand their dietary habits. She decides to ask the next 50 patients that she sees about what kind of foods they like to eat.

 

Explain why the type of sampling that was chosen for the survey might lead to biased results.

If Dr. Aleman wants to learn about the eating habits of all of her patients, she needs to choose a sample so that each of her patients has an equally likely chance of being surveyed. The type of survey that Dr. Aleman has chosen has selection bias because she is using a convenience sample.

11.  A brief account of an experiment is given below:

 

500 subjects, representing a cross-section of society, are chosen to take part in an experiment.  250 of them are chosen at random and instructed to take a vitamin C pill every morning for six months.  The remaining 250 are given a placebo to take every morning for six months.  The subjects do not know whether they are taking the vitamin C or the placebo.  At the end of six months the mean number of colds of the subjects that took vitamin C is significantly lower than those that took the placebo.  The experimenters release a statement that says that vitamin C causes a lower number of colds. 

 

Do you agree with the experimenters conclusions?  Explain.

 

Since the experiment includes randomization, control, and has used enough subjects, causation is an appropriate conclusion.

 

 

 

12.  Mrs. Wheeler, the school librarian, wants to determine how many students use the library on a regular basis. What type of sampling method (stratified, simple random, convenience sample, interval sample) would she use if she chose to:

                         

interval sample      A. Choose every 3rd student who enters the library on Tuesday.

                         

simple random       B. Use a random number generator to randomly select 50 students from the school’s attendance roster.

                         

stratified                C. Randomly select 5 students from every student organization.

                         

convenience sampleD. Stand outside the school door and interview the first 50 students who arrive at school on Wednesday.

 

 

13. Describe the following pair of events as dependent or independent.  Explain your answer.

      Two six-sided dice—one red and one blue—are rolled at the same time.

            Event 1:  The red die shows a 4.

            Event 2:  The blue die shows a 4.

      The events are independent.  The probability of event 2 is 1/6 regardless of whether event 1 has occurred.

 

14. Describe the following pair of events as mutually exclusive or not mutually exclusive.  If they are mutually exclusive, state whether they are complementary.  Explain your answer.

      One six-sided die is rolled.

            Event 1:  The die shows an even number.

            Event 2:  The die shows an odd number.

      The events are mutually exclusive and complementary.  They cannot occur at the same time and either one will occur or the other will.

15. Each letter for the words STATISTICS and PROBABILITY is written on a card. All of the cards are placed in a bag.

__3/21 = 1/7 ~ 14%_______       A. What is the probability of randomly drawing the letter S from

the bag?

 

___(1/7)*(1/7) = 1/49____         B. What is the probability of drawing an S, returning it to the bag,

and then drawing another S?

 

 

___(1/7)*(2/20) = 2/140=1/70   C. What is the probability of drawing an S, not returning it to the    

                                                     bag, and then drawing another S?

 

 

___(3/21)+(4/21) = 7/21=1/3_   D. What is the probability of drawing either an S or a T?

 

16. A study of 100 adults found 65 that own dogs, 40 that own cats, and 20 that own dogs and cats.

own cats
 
      A.  Draw a Venn Diagram that depicts the above relationship.

 

 

 


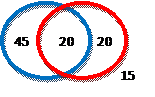
      B.  One of the adults in the study is selected at random.  Find the probability that this person owns a dog.

                        65/100 = 13/20

      C.  One of the cat-owners in the study is selected at random.  Find the probability that this person owns a dog.

                        20/40 = 1/2

      D.  Using the given information, is the event a person owns a dog independent of the event a person owns a dog?

            They are not independent.  If they were independent, the probability of a person owns a dog would be the same as the person owns a dog given that the person owns a cat.

17. There are 10 students—6 boys and 4 girls in the math club.

      A.  How many ways can the 10 students line up for a picture?

            10! = 3,628,800

      B.  A competition team consists of four students without specific designations.  Explain whether this is an example of a combination or permutation and find the number of teams that can be formed.

            combinations—the order the four are selected is not relevant.

            10C4 =210

      C.  One boy and one girl will be crowned math club king and queen.  How many different couples are possible?

            6 ( 4) = 24