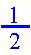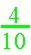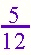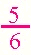 |
What's My Order? |
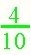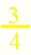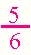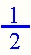 |
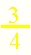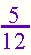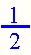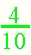 |
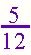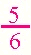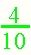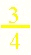 |
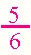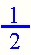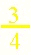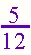 |
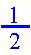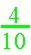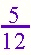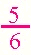 |
What's My Order? |
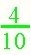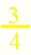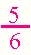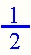 |
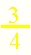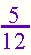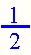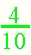 |
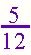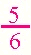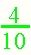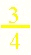 |
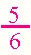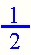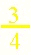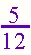 |
Part 1: Ordering Fractions with Like Denominators * *Katie and Raj both have the same size submarine sandwich. Each sandwich is cut into 8 equal slices. Katie is going to eat 2 pieces of her sandwich. Raj is going to eat 4 pieces of his sandwich. Using the virtual fraction applet, the following image can be constructed. Notice the slider can help students count out the fractions along the rectangle. Students should be able to identify that Katie will eat 2/8 of her sandwich and Raj will eat 4/8 of his sandwich. As the students use the arrows to shade in the rectangle, they will see the name of the fractional part of the whole on the right. They also are forced at this point to see the rectangles in an order which eventually should transfer to using a number line model.  Raj eats more of his sandwich. Keep in mind that students need to discuss that the sandwiches are the same size, so the "unit" is the same for both Katie and Raj. They also need to discuss that the sandwiches were cut into equal pieces. Many students will be set in their thinking that since 2 is less than 4, Katie eats less food. While this is true for like denominators, students need to add into their thoughts and discussions that they are comparing the same size pieces of the sandwich. Given that the manipulatives are virtual, ask students to open up the Pattern Block Applet and the Integer Rods Applet to see if they could represent the sandwiches with those manipulatives. If using the physical manipulatives, one can see that this could easily get out of control and student might be confused with all of the different pieces. With the virtual manipulatives, students can switch quickly from applet to applet and explore why one manipulative perhaps is better than another for their investigation. There is number sense thinking going on when one make a choice about which pieces to use out of a manipulative for an investigation. Have students write out sentences and then write out the math symbols. This helps build the foundation for their problem solving skills later in Algebra. Part 1 Follow up QuestionsOne observation that can be made is that the part of the sandwich that Raj will eat is twice as big as Katie's portion. This can be seen with the virtual fractions and students should be drawn into writing out the math! They can start to establish that 2* 2/8 = 4/8. Students need to put this in perspective. Some students will stay with the familiar and write 2*2 = 4. Some will get frustrated because they are giving a correct logical answer with respect to whole number thinking. They need to be aware that we can say things from different perspectives and they need to be able to communicate from different points of view or different number sets. This needs to be established on a simple level. Students encounter different number types in life such as fractions, decimals, and percentages and if they do not have a good basic foundation about these changes of perspectives, they soon get lost and give up. Students are asked if Katie took 2 pieces and Raj took 4 pieces of the same sandwich, would one sandwich be enough to feed them? Although the virtual fraction applet does not allow for the students to move the pieces "off of the sandwich," students can use the arrow buttons to "add on" Raj's pieces to Katie "sandwich." Point out that the pieces are all alike so it is a simple add on problem and only 6 of the 8 pieces will be eaten! At this point, the symbols 2/8 + 4/8 = 6/8 can be written. Again, some students will not see the need to use fractions and will be set on writing 2 + 4 = 6. This again is a situation where the student needs to learn to change perspectives. What is one unit in this problem, the sandwich or the pieces? This is not a one day activity for many students and this idea needs to be addressed over and over when developing their number sense using fractions.Part 1 Problems |
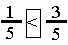 One fifth is less than three fifths.  |
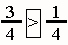
Three fourths is greater than 1 fourth. 
|
|
Answers will vary. Look for an understanding of the unit in the problem. Make sure that the students clearly state the unit which is broken up into 5 pieces. Encourage students to rewrite their work to refine their thinking after discussion about their response. Students could talk about their stories in a group and each could explain the "math" in their story. This activity amounts to making up a "word problem" or "story problem" about the numbers. Invite students to think about where they might see these number comparison used outside of school. |
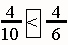  |
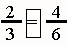
 |
|
Answers will vary. Look for an understanding of the unit in the problem. Make sure that the students clearly state which unit is broken up into 10 pieces and which unit is broken into 6 pieces. Encourage students to rewrite their work to refine their thinking after discussion about their response. Students could talk about their stories in a group and each could explain the "math" in their story. This activity amounts to making up a "word problem" or "story problem" about the numbers. Invite students to think about where they might see these number comparison used outside of school. Note: The denominators in this problem do not "match up." Invite students to include addition into their story and see how they approach this problem. |
|
These fractions are equivalent. Give students other equivalent fractions to see using the applet. Ask them to reason out when two fractions will be equivalent. Depending on grade level, this can include how "write the math!" |
*Sandwich gif from http://www.go.dlr.de/wt/dv/ig/icons/funet.html Copyright  2001 by
Margo Lynn Mankus 2001 by
Margo Lynn Mankus
|