Project 5 - Image Compression

Matthew Herman

Computer Problems 11.2 #3-6
11.2 Computer Problem 3
Obtain a grayscale image file of your choice, and use the imread command to import into MATLAB. Crop the resulting matrix so into MATLAB. Crop the resulting matrix so that each dimension is a multiple of 8. If necessary, converting a color RGB image to gray scale can be accomplished by the standard formula (11.15).
(a) Extract an 8 � 8 pixel block, for example, by using the MATLAB command xb=x(81:88,81:88). Display the block with the imagesc command.
(b) Apply the 2D-DCT.
(c) Quantize by using linear quantization with p = 1,2, and 4. Print out each YQ.
(d) Reconstruct the block by using the inverse 2D-DCT, and compare with the original. Use MATLAB commands colormap(gray) and imagesc(X,[0 255]).
(e) Carry out (a)�(d) for all 8 � 8 blocks, and reconstitute the image in each case.
11.2 Computer Problem
Carry out the steps of Computer Problem 3, but quantize by the JPEG-suggested matrix (11.25) with p = 1.
compress with JPEG matrix
11.2 Computer Problem
Obtain a color image file of your choice. Carry out the steps of Computer Problem 3 for colors R, G, and B separately, using linear quantization, and recombine as a color image.
RGB with JPEG matrix
6. Obtain a color image, and transform the RGB values to luminance/color difference coordinates. Carry out the steps of Computer Problem 3 for Y , U, and V separately by using JPEG quantization, and recombine as a color image.
Trying with larger image (1200x1200)

Computer Problems 11.2 #3-6

11.2 Computer Problem 3

Obtain a grayscale image file of your choice, and use the imread command to import into MATLAB. Crop the resulting matrix so into MATLAB. Crop the resulting matrix so that each dimension is a multiple of 8. If necessary, converting a color RGB image to gray scale can be accomplished by the standard formula (11.15).

x = imread('boat.png');
figure(1)
imagesc(x)
title('Original image 512x512')

(a) Extract an 8 � 8 pixel block, for example, by using the MATLAB command xb=x(81:88,81:88). Display the block with the imagesc command.

% Full image
figure(2)
x = double(x);
r = x(:,:,1);
g = x(:,:,2);
b = x(:,:,3);
xgray=0.2126*r+0.7152*g+0.0722*b;
xgray = uint8(xgray);
imagesc(xgray);
colormap(gray);
title('Image in grayscale')

% 8x8 image
figure(3)
xb=x(81:88,81:88);

(b) Apply the 2D-DCT.

f1 = @fun_dct;
C = f1(xb)

% function C=fun_dct(X)
% [m,n]=size(X);n=m;
% for i=2:n
%     for j=1:n
%         C(i,j)=sqrt(2/n)*cos((i-1)*(j-1/2)*pi/n);
%     end
% end
% C(1,1:n)=ones(1,n)/sqrt(n);

C =

  Columns 1 through 7

    0.3536    0.3536    0.3536    0.3536    0.3536    0.3536    0.3536
    0.4904    0.4157    0.2778    0.0975   -0.0975   -0.2778   -0.4157
    0.4619    0.1913   -0.1913   -0.4619   -0.4619   -0.1913    0.1913
    0.4157   -0.0975   -0.4904   -0.2778    0.2778    0.4904    0.0975
    0.3536   -0.3536   -0.3536    0.3536    0.3536   -0.3536   -0.3536
    0.2778   -0.4904    0.0975    0.4157   -0.4157   -0.0975    0.4904
    0.1913   -0.4619    0.4619   -0.1913   -0.1913    0.4619   -0.4619
    0.0975   -0.2778    0.4157   -0.4904    0.4904   -0.4157    0.2778

  Column 8

    0.3536
   -0.4904
    0.4619
   -0.4157
    0.3536
   -0.2778
    0.1913
   -0.0975

(c) Quantize by using linear quantization with p = 1,2, and 4. Print out each YQ.

p = 1;
Q1 = p*8./hilb(8);

p = 2;
Q2 = p*8./hilb(8);

p = 4;
Q4 = p*8./hilb(8);

Xd=double(xb);
Xc=Xd-128;
Y=C*Xc*C';

Q1
Yq1=round(Y./Q1)
Q2
Yq2=round(Y./Q2)
Q4
Yq4=round(Y./Q4)

Q1 =

     8    16    24    32    40    48    56    64
    16    24    32    40    48    56    64    72
    24    32    40    48    56    64    72    80
    32    40    48    56    64    72    80    88
    40    48    56    64    72    80    88    96
    48    56    64    72    80    88    96   104
    56    64    72    80    88    96   104   112
    64    72    80    88    96   104   112   120


Yq1 =

  -114     1     0     0     0     0     0     0
    -2     0    -1     0     0     0     0     0
     0     1     0    -1     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0


Q2 =

    16    32    48    64    80    96   112   128
    32    48    64    80    96   112   128   144
    48    64    80    96   112   128   144   160
    64    80    96   112   128   144   160   176
    80    96   112   128   144   160   176   192
    96   112   128   144   160   176   192   208
   112   128   144   160   176   192   208   224
   128   144   160   176   192   208   224   240


Yq2 =

   -57     1     0     0     0     0     0     0
    -1     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0


Q4 =

    32    64    96   128   160   192   224   256
    64    96   128   160   192   224   256   288
    96   128   160   192   224   256   288   320
   128   160   192   224   256   288   320   352
   160   192   224   256   288   320   352   384
   192   224   256   288   320   352   384   416
   224   256   288   320   352   384   416   448
   256   288   320   352   384   416   448   480


Yq4 =

   -29     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0

(d) Reconstruct the block by using the inverse 2D-DCT, and compare with the original. Use MATLAB commands colormap(gray) and imagesc(X,[0 255]).

imagesc(xb);
colormap(gray);
title('8x8 block of grayscale image')

Ydq1=Yq1.*Q1;
Xdq1=C'*Ydq1*C;
Xe1=Xdq1+128;
Xf1=uint8(Xe1);

Ydq2=Yq2.*Q2;
Xdq2=C'*Ydq2*C;
Xe2=Xdq2+128;
Xf2=uint8(Xe2);

Ydq4=Yq4.*Q4;
Xdq4=C'*Ydq4*C;
Xe4=Xdq4+128;
Xf4=uint8(Xe4);

figure(4)
imagesc(Xf1)
colormap(gray)
title('Grayscale block p=1')

figure(5)
imagesc(Xf2)
colormap(gray)
title('Grayscale block p=2')

figure(6)
imagesc(Xf4)
colormap(gray)
title('Grayscale block p=4')

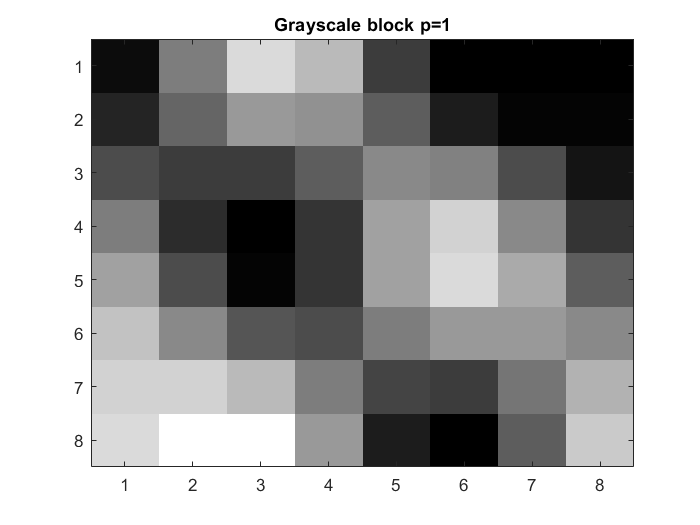
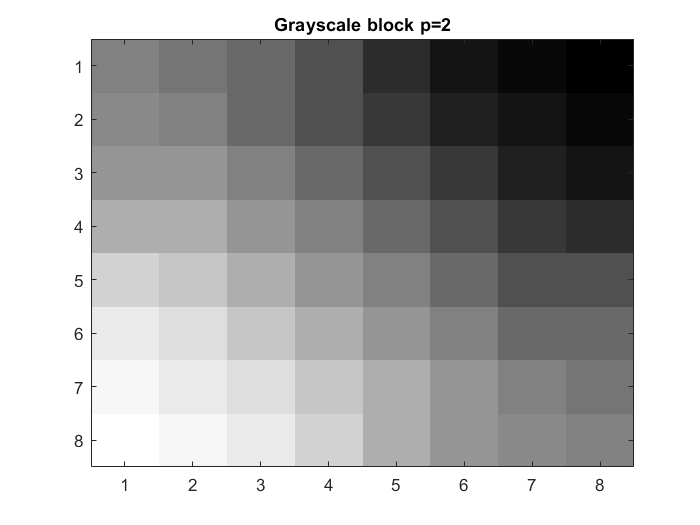
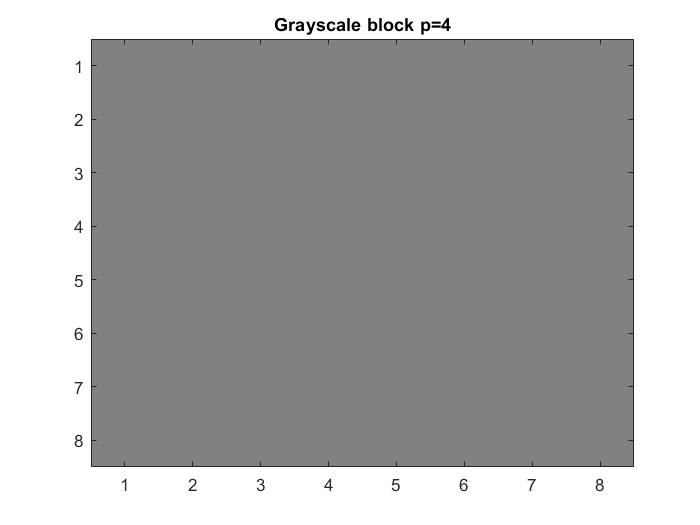
(e) Carry out (a)�(d) for all 8 � 8 blocks, and reconstitute the image in each case.

function Xf=compress(image,p) % x == image file x = imread(image); % p == loss parameter [m,n]=size(x);n=m; Q = p*8./hilb(8); x = double(x); r = x(:,:,1); g = x(:,:,2); b = x(:,:,3); xgray=0.2126*r+0.7152*g+0.0722*b; for i = 1:8:m for j = 1:8:n Xb = xgray(i:i+7,j:j+7); C = fun_dct(Xb); Xd=double(Xb); Xc=Xd-128; Y=C*Xc*C'; Yq=round(Y./Q); Ydq = Yq.*Q; Xd = C'*Ydq*C; Xe=Xd+128; Xf(i:i+7,j:j+7)=Xe; end end imagesc(uint8(Xf)) colormap(gray)

figure(7)
p1 = compress('boat.png',1);
title('Grayscale p=1')

figure(8)
p2 = compress('boat.png',2);
title('Grayscale p=2')

figure(9)
p4 = compress('boat.png',4);
title('Grayscale p=4')

figure(10)
p16 = compress('boat.png',16);
title('Grayscale p=16')

11.2 Computer Problem

Carry out the steps of Computer Problem 3, but quantize by the JPEG-suggested matrix (11.25) with p = 1.

compress with JPEG matrix

function Xf=compressJPEG(image,p) % x == image file x = imread(image); % p == loss parameter [m,n]=size(x);n=m; Qy=p*[16 11 10 16 24 40 51 61; ... 12 12 14 19 26 58 60 55; ... 14 13 16 24 40 57 69 56; ... 14 17 22 29 51 87 80 62; ... 18 22 37 56 68 109 103 77; ... 24 35 55 64 81 104 113 92; ... 49 64 78 87 103 121 120 101; ... 72 92 95 98 112 100 103 99]; x = double(x); r = x(:,:,1); g = x(:,:,2); b = x(:,:,3); xgray=0.2126*r+0.7152*g+0.0722*b; for i = 1:8:m for j = 1:8:n Xb = xgray(i:i+7,j:j+7); C = fun_dct(Xb); Xd=double(Xb); Xc=Xd-128; Y=C*Xc*C'; Yq=round(Y./Qy); Ydq = Yq.*Qy; Xd = C'*Ydq*C; Xe=Xd+128; Xf(i:i+7,j:j+7)=Xe; end end imagesc(uint8(Xf)) colormap(gray)

figure(11)
JPEG1 = compressJPEG('boat.png',1);
title('JPEG p=1')

figure(12)
JPEG2 = compressJPEG('boat.png',2);
title('JPEG p=2')

figure(13)
JPEG4 = compressJPEG('boat.png',4);
title('JPEG p=4')

figure(14)
JPEG16 = compressJPEG('boat.png',16);
title('JPEG p=16')

11.2 Computer Problem

Obtain a color image file of your choice. Carry out the steps of Computer Problem 3 for colors R, G, and B separately, using linear quantization, and recombine as a color image.

function Xf=compressRGB(image,p) % x == image file x = imread(image); % p == loss parameter [m,n]=size(x);n=m; Q = p*8./hilb(8); x = double(x);

r = x(:,:,1); g = x(:,:,2); b = x(:,:,3);

for i = 1:8:m for j = 1:8:n Xr = r(i:i+7,j:j+7); Xg = g(i:i+7,j:j+7); Xb = b(i:i+7,j:j+7);

       Cr = fun_dct(Xr);
       Cg = fun_dct(Xg);
       Cb = fun_dct(Xb);

       Xdr = double(Xr);
       Xdg = double(Xg);
       Xdb = double(Xb);

       Xcr = Xdr-128;
       Xcg = Xdg-128;
       Xcb = Xdb-128;

       Yr = Cr*Xcr*Cr';
       Yg = Cg*Xcg*Cg';
       Yb = Cb*Xcb*Cb';

       Yqr = round(Yr./Q);
       Yqg = round(Yg./Q);
       Yqb = round(Yb./Q);

       Ydqr = Yqr.*Q;
       Ydqg = Yqg.*Q;
       Ydqb = Yqb.*Q;

       Xdr = Cr'*Ydqr*Cr;
       Xdg = Cg'*Ydqg*Cg;
       Xdb = Cb'*Ydqb*Cb;

       Xer = Xdr+128;
       Xeg = Xdg+128;
       Xeb = Xdb+128;

       Xf(i:i+7,j:j+7,1) = Xer;
       Xf(i:i+7,j:j+7,2) = Xeg;
       Xf(i:i+7,j:j+7,3) = Xeb;
   end
end
imagesc(uint8(Xf))

x = imread('boat.png');
figure(15)
imagesc(x)
title('Original color image 512x512')

figure(16)
RGB1 = compressRGB('boat.png',1);
title('RGB p=1')

figure(17)
RGB2 = compressRGB('boat.png',2);
title('RGB p=2')

figure(18)
RGB4 = compressRGB('boat.png',4);
title('RGB p=4')

figure(19)
RGB16 = compressRGB('boat.png',16);
title('RGB p=16')

RGB with JPEG matrix

function Xf=compressJPEGRGB(image,p) % x == image file x = imread(image); % p == loss parameter [m,n]=size(x);n=m; Q=p*[16 11 10 16 24 40 51 61; ... 12 12 14 19 26 58 60 55; ... 14 13 16 24 40 57 69 56; ... 14 17 22 29 51 87 80 62; ... 18 22 37 56 68 109 103 77; ... 24 35 55 64 81 104 113 92; ... 49 64 78 87 103 121 120 101; ... 72 92 95 98 112 100 103 99]; x = double(x);

r = x(:,:,1); g = x(:,:,2); b = x(:,:,3);

for i = 1:8:m for j = 1:8:n Xr = r(i:i+7,j:j+7); Xg = g(i:i+7,j:j+7); Xb = b(i:i+7,j:j+7);

       Cr = fun_dct(Xr);
       Cg = fun_dct(Xg);
       Cb = fun_dct(Xb);

       Xdr = double(Xr);
       Xdg = double(Xg);
       Xdb = double(Xb);

       Xcr = Xdr-128;
       Xcg = Xdg-128;
       Xcb = Xdb-128;

       Yr = Cr*Xcr*Cr';
       Yg = Cg*Xcg*Cg';
       Yb = Cb*Xcb*Cb';

       Yqr = round(Yr./Q);
       Yqg = round(Yg./Q);
       Yqb = round(Yb./Q);

       Ydqr = Yqr.*Q;
       Ydqg = Yqg.*Q;
       Ydqb = Yqb.*Q;

       Xdr = Cr'*Ydqr*Cr;
       Xdg = Cg'*Ydqg*Cg;
       Xdb = Cb'*Ydqb*Cb;

       Xer = Xdr+128;
       Xeg = Xdg+128;
       Xeb = Xdb+128;

       Xf(i:i+7,j:j+7,1) = Xer;
       Xf(i:i+7,j:j+7,2) = Xeg;
       Xf(i:i+7,j:j+7,3) = Xeb;
   end
end
imagesc(uint8(Xf))

figure(20)
JPEGRGB1 = compressJPEGRGB('boat.png',1);
title('JPEG RGB p=1')

figure(21)
JPEGRGB2 = compressJPEGRGB('boat.png',2);
title('JPEG RGB p=2')

figure(22)
JPEGRGB4 = compressJPEGRGB('boat.png',4);
title('JPEG RGB p=4')

figure(23)
JPEGRGB16 = compressJPEGRGB('boat.png',16);
title('JPEG RGB p=16')

6. Obtain a color image, and transform the RGB values to luminance/color difference coordinates. Carry out the steps of Computer Problem 3 for Y , U, and V separately by using JPEG quantization, and recombine as a color image.

function Xf=compressYUV(image,p) % x == image file x = imread(image); % p == loss parameter [m,n]=size(x);n=m; Q=p*[16 11 10 16 24 40 51 61; ... 12 12 14 19 26 58 60 55; ... 14 13 16 24 40 57 69 56; ... 14 17 22 29 51 87 80 62; ... 18 22 37 56 68 109 103 77; ... 24 35 55 64 81 104 113 92; ... 49 64 78 87 103 121 120 101; ... 72 92 95 98 112 100 103 99]; x = double(x);

r = x(:,:,1); g = x(:,:,2); b = x(:,:,3);

Y = 0.299*r+0.587*g+0.144*b; U = b - Y; V = r - Y;

for i = 1:8:m for j = 1:8:n XY = Y(i:i+7,j:j+7); XU = U(i:i+7,j:j+7); XV = V(i:i+7,j:j+7);

       CY = fun_dct(XY);
       CU = fun_dct(XU);
       CV = fun_dct(XV);

       XdY = double(XY);
       XdU = double(XU);
       XdV = double(XV);

       XcY = XdY-128;
       XcU = XdU-128;
       XcV = XdV-128;

       YY = CY*XcY*CY';
       YU = CU*XcU*CU';
       YV = CV*XcV*CV';

       YqY = round(YY./Q);
       YqU = round(YU./Q);
       YqV = round(YV./Q);

       YdqY = YqY.*Q;
       YdqU = YqU.*Q;
       YdqV = YqV.*Q;

       XdY = CY'*YdqY*CY;
       XdU = CU'*YdqU*CU;
       XdV = CV'*YdqV*CV;

       XeY = XdY+128;
       XeU = XdU+128;
       XeV = XdV+128;

       %red
       R = XeY + XeV;
       %blue
       B = XeU + XeY;
       %green
       G = (XeY - 0.299*R - 0.114*B)/0.587;

       Xf(i:i+7,j:j+7,1) = R;
       Xf(i:i+7,j:j+7,2) = G;
       Xf(i:i+7,j:j+7,3) = B;
   end
end
imagesc(uint8(Xf))

figure(24)
YUV1 = compressYUV('boat.png',1);
title('YUV p=1')

figure(25)
YUV2 = compressYUV('boat.png',2);
title('YUV p=2')

figure(26)
YUV4 = compressYUV('boat.png',4);
title('YUV p=4')

figure(27)
YUV16 = compressYUV('boat.png',16);
title('YUV p=16')

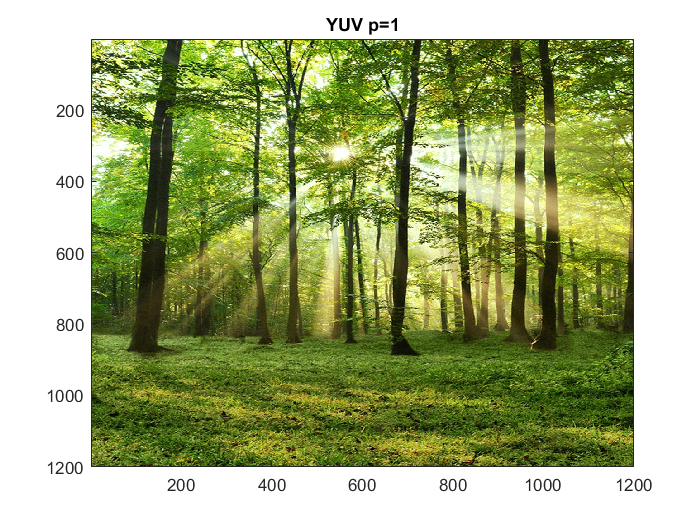
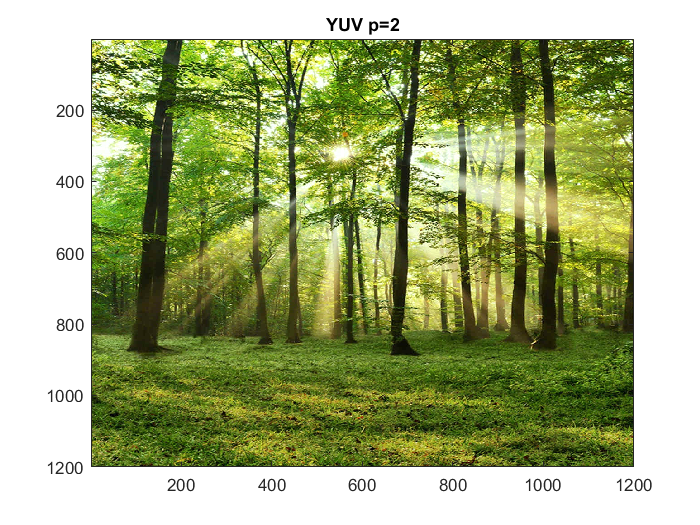
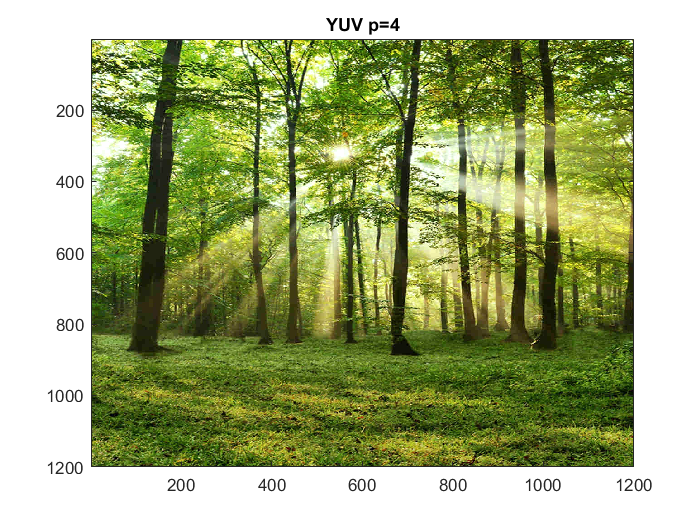
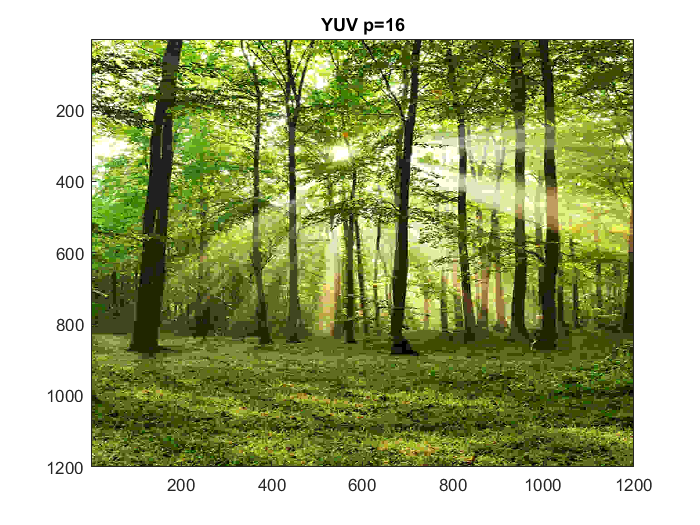
Trying with larger image (1200x1200)

figure(28)
x = imread('trees.png');
imagesc(x)
title('Original color image 1200x1200')

figure(29)
bigYUV1 = compressYUV('trees.png',1);
title('YUV p=1')

figure(30)
bigYUV2 = compressYUV('trees.png',2);
title('YUV p=2')

figure(31)
bigYUV4 = compressYUV('trees.png',4);
title('YUV p=4')

figure(32)
bigYUV16 = compressYUV('trees.png',16);
title('YUV p=16')

Project 5 - Image Compression

Contents

Computer Problems 11.2 #3-6

11.2 Computer Problem 3

(a) Extract an 8 � 8 pixel block, for example, by using the MATLAB command xb=x(81:88,81:88). Display the block with the imagesc command.

(b) Apply the 2D-DCT.

(c) Quantize by using linear quantization with p = 1,2, and 4. Print out each YQ.

(d) Reconstruct the block by using the inverse 2D-DCT, and compare with the original. Use MATLAB commands colormap(gray) and imagesc(X,[0 255]).

(e) Carry out (a)�(d) for all 8 � 8 blocks, and reconstitute the image in each case.

11.2 Computer Problem

Carry out the steps of Computer Problem 3, but quantize by the JPEG-suggested matrix (11.25) with p = 1.

compress with JPEG matrix

11.2 Computer Problem

Obtain a color image file of your choice. Carry out the steps of Computer Problem 3 for colors R, G, and B separately, using linear quantization, and recombine as a color image.

RGB with JPEG matrix

6. Obtain a color image, and transform the RGB values to luminance/color difference coordinates. Carry out the steps of Computer Problem 3 for Y , U, and V separately by using JPEG quantization, and recombine as a color image.

Trying with larger image (1200x1200)