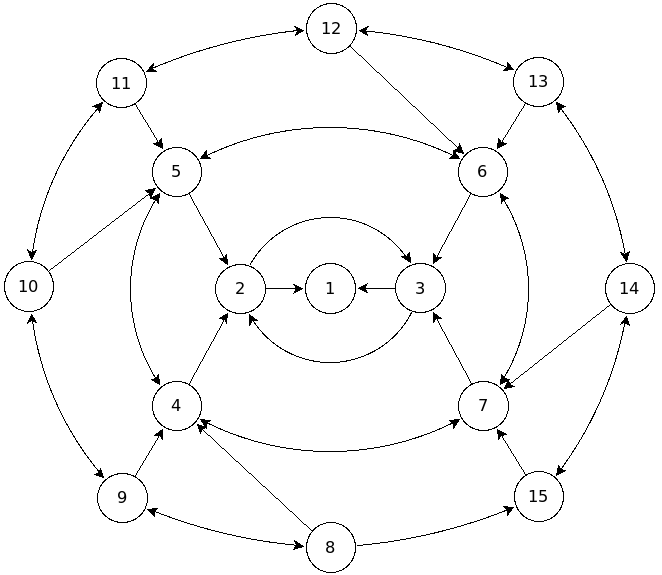
This network consists of rings containing \(2^i\) nodes. The user may either move along the edge of the ring or move inward to the next smaller ring. Movement outward is prevented, and the network eventually collapses in a single node with no outbound links. Its adjacency matrix is: \[A = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \end{bmatrix}\] Before the page ranks could even be computed, the MATLAB code needed to be modified to handle nodes with no outbound links. This is accomplished by adding a link from such a node to every other node in the network with \(1/n\) probability. The technique was taken from a slideshow presentation on PageRank in a Dartmouth class on the subject. The modified code (rankup.m) was then used to evaluate the network, beginning with different values of q. \[\begin{align} p &= \begin{bmatrix} 0.1144 \\ 0.1152 \\ 0.1152 \\ 0.0878 \\ 0.0878 \\ 0.0878 \\ 0.0878 \\ 0.0380 \\ 0.0380 \\ 0.0380 \\ 0.0380 \\ 0.0380 \\ 0.0380 \\ 0.0380 \\ 0.0380 \end{bmatrix} & p_{q=0.0} &= \begin{bmatrix} 0.1456 \\ 0.1359 \\ 0.1359 \\ 0.0874 \\ 0.0874 \\ 0.0874 \\ 0.0874 \\ 0.0291 \\ 0.0291 \\ 0.0291 \\ 0.0291 \\ 0.0291 \\ 0.0291 \\ 0.0291 \\ 0.0291 \end{bmatrix} & p_{q=0.5} &= \begin{bmatrix} 0.0778 \\ 0.0838 \\ 0.0838 \\ 0.0808 \\ 0.0808 \\ 0.0808 \\ 0.0808 \\ 0.0539 \\ 0.0539 \\ 0.0539 \\ 0.0539 \\ 0.0539 \\ 0.0539 \\ 0.0539 \\ 0.0539 \end{bmatrix} \end{align}\] Despite the fact that all links eventually lead to node 1, with the standard jump probability it is slightly more likely to be on either node 2 or 3. If the jump probability is removed, however, then the node 1 does achieve the highest page rank. But if the jump probability is emphasized, node 1's page rank falls below that of the node 4 ring. The page ranks with node 1 removed are: \[\begin{align} p &= \begin{bmatrix} 0.1144 \\ 0.1152 \\ 0.1152 \\ 0.0878 \\ 0.0878 \\ 0.0878 \\ 0.0878 \\ 0.0380 \\ 0.0380 \\ 0.0380 \\ 0.0380 \\ 0.0380 \\ 0.0380 \\ 0.0380 \\ 0.0380 \end{bmatrix} & p_{new} = \begin{bmatrix} \\ 0.2870 \\ 0.2870 \\ 0.0571 \\ 0.0571 \\ 0.0571 \\ 0.0571 \\ 0.0247 \\ 0.0247 \\ 0.0247 \\ 0.0247 \\ 0.0247 \\ 0.0247 \\ 0.0247 \\ 0.0247 \end{bmatrix} \end{align}\] Interestingly, with node 1 removed nodes 2 and 3 dominate the network to an even greater extent than nodes 1,2 and 3 did together in the original network. Whereas there was a roughly 34% chance of being on one of the three center nodes in the original network, there is about a 57% chance of being on either node 2 or 3 in the new network. Without node 1 existing to effectively terminate a link sequence, the user is more likely to bounce back and forth between nodes 2 and 3.