Color Image Compression

Kathleen McLane

Color Images

The last two questions for this project involved performing image compression on a color image. To do this, the image had to be separated into the three different colors, red, green, and blue.

Similar to the first question, an 8x8 pixel block was taken from the picture, and the 2D-DCT was applied to it. The code for this can be seen here where steps were added to take care of the colors. Since this was a color image, the same steps from part one were done, but it was completed in a loop, such that the process was applied to the red color, then the blue color, and then the green color. Below are the \(Y_Q\) print outs for p=1,2, and 4, after each color was completed. First, here is the 8x8 image that was taken:

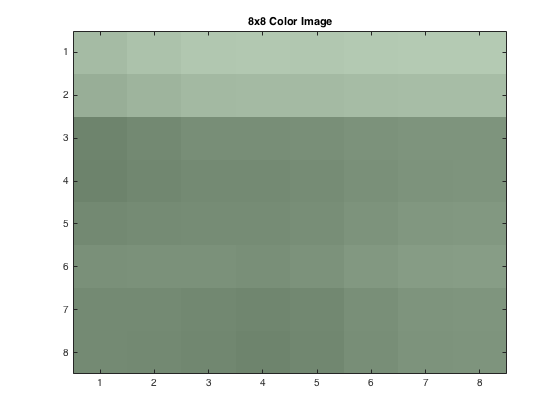
From here, the new 8x8 blocks could be found, such that each one was different. These plots can be seen below:

After the \(Y_Q\) matrices were found, the inverse was taken for each case, and the completed pictures were reconstructed. The new images that have gone through compression can be seen below. The p=1 case looks the best, and the p=4 case appears the most pixelated.

Luminance and Color Difference

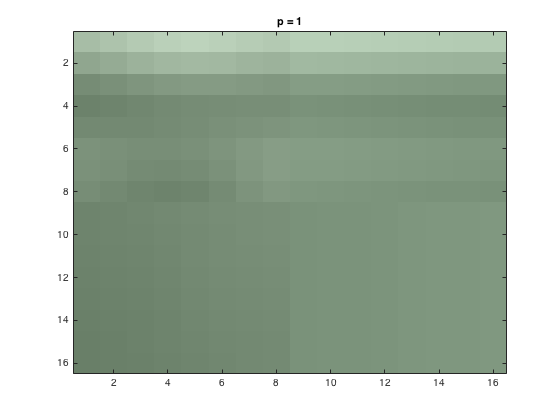
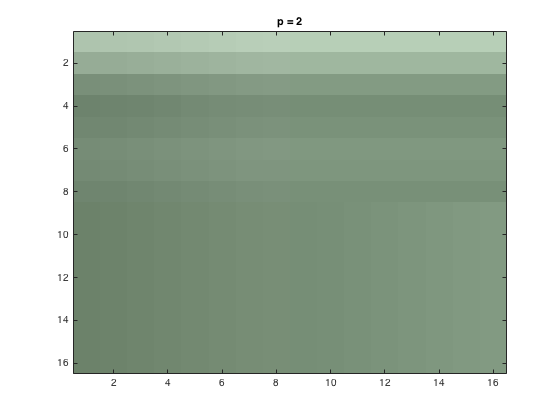
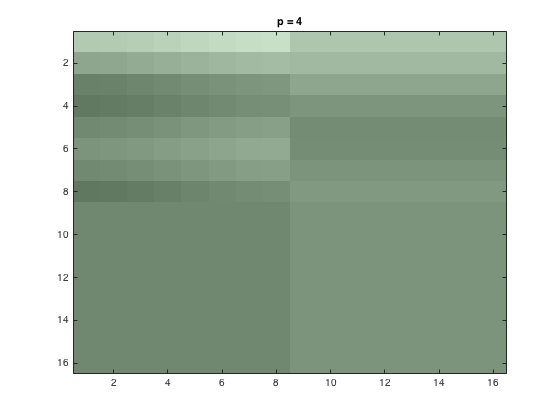
The next part of the problem involved completing the above steps, but the RGB values had luminance and color difference coordinates. This involved carrying out the steps of part 1 for the coordinates separately, and then using JPEG quantization to recombine the color image. The luminance is defined as: \begin{align*} Y=0.299R+0.587G+0.114B \end{align*} While the color difference is defined as: \begin{align*} U=B-Y\\ V=R-Y\\ \end{align*} The code for this new change can be seen here. After this effect was changed, the three loss parameters(p=1,2,4) were again looked at, and the new \(Y_Q\) plots were produced. They can be seen below: -Y_Q images for 1, 2, 4- Once these images were produced, the inverse 2D-DCT was used again, and the image was put back together. The new compressed color image for each case can be seen below.