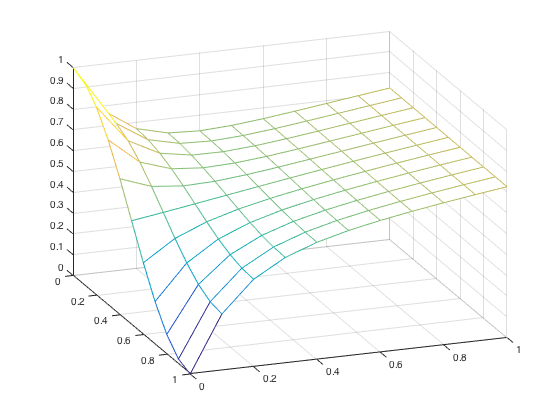
Before beginning the project on Fisher's Equation, we first tested the code presented for Burger's Equation. Burger's equation is \begin{align*} u_t+uu_{x}=Du_{xx} \end{align*} This equation is nonlinear due to the \(uu_{x}\) term, and is a simplified model of fluid flow. If one were to solve for this, one way to go about this is a Backward Difference Equation with Newton iteration. Doing this, the problem would look as follows: To solve this, we used the code to solve Burger's equation, as given in the book burgers.m. From this, the following graph was produced showing the solution heading toward the equilibrium solution.

Once the code for Burger's equation was checked, the code for Fisher's equation was recreated. The Fisher's equation
used can be seen on the home page with \(f(u)=u(1-u)\). Using the previous code, only a couple lines of code was changed, as well
as changing the initial conditions to Neumann Boundary Conditions. The code for this can be seen here.
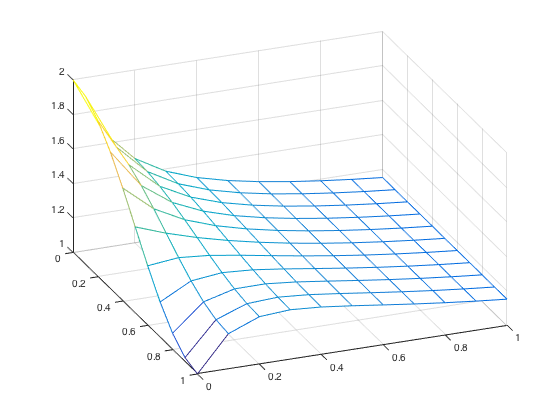
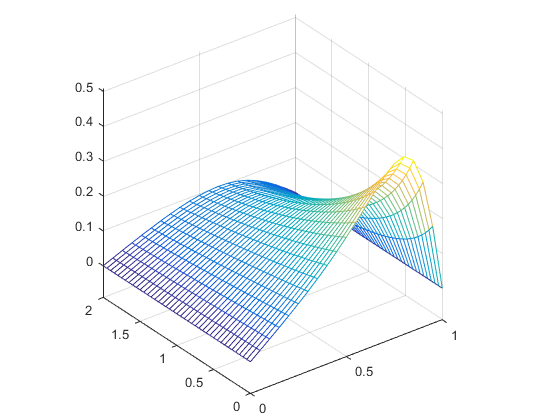
From this code, two different example graphs were produced. The first is for the initial condition \(u(x,0)=0.5+0.5cos(\pi x)\),
and the second is for the initial condition \(u(x,0)=1.5+0.5cos(\pi x)\).
Solution where the initial condition is \(u(x,0)=0.5+0.5cos(\pi x)\)