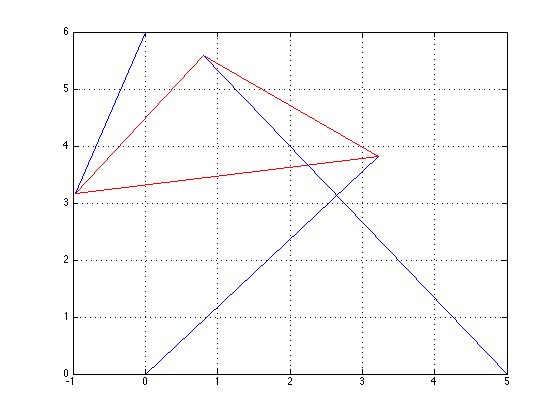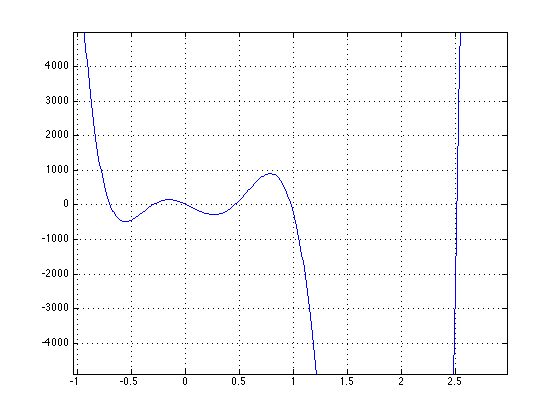
Part 5 asked us to solve the forward kinematics problem for the planar Stewart Platform, similar to part 4, but this time p2 had to equal a value close to 7. We chose to use 6.99, as this would allow us to find 6 different poses. The same type of methodology was used as in part 4, and the diary can be seen here: diary5.rtf. The plot of \(f(\theta)\) vs. \(\theta\) can be seen below, and the \(\theta\) values at which the zeros occurred are: \(\theta\) = -0.6969, -0.3035, 0.0139, 0.4560, 0.9780, and 2.5128.

\(\theta\) = -0.6969, x=-4.2554, y=2.6252
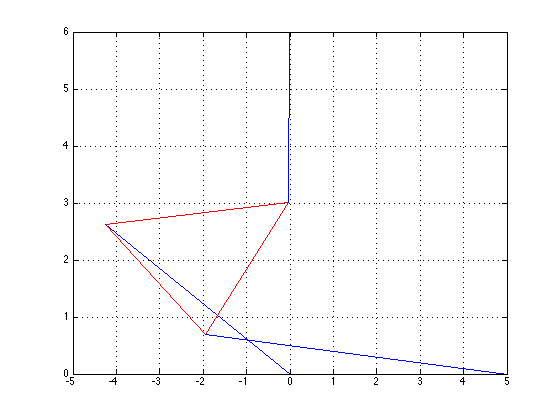
\(\theta\)=-0.3035, x=-4.8446, y=1.2368
\(\theta\)=0.0139, x=-4.9487, y=0.7143
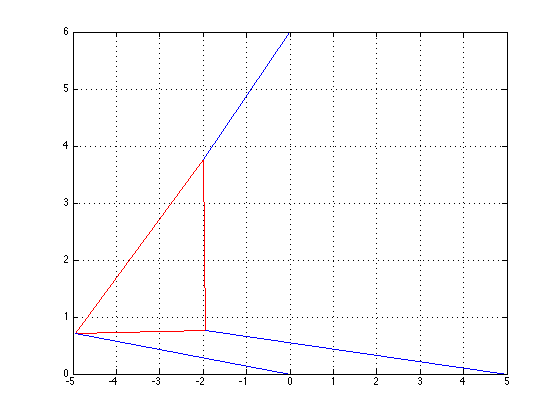
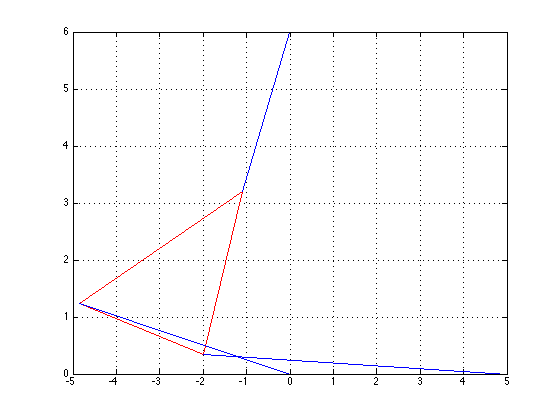
\(\theta\)=0.4560, x=-0.8155, y=4.9327
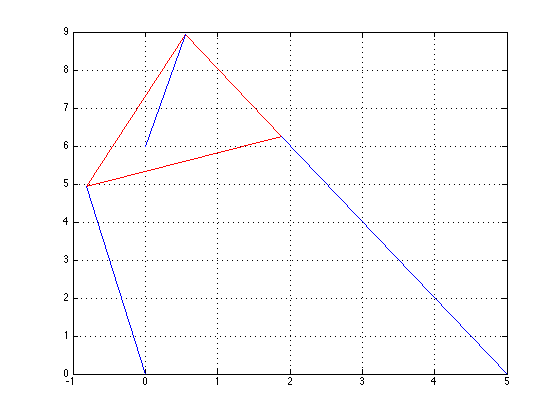
\(\theta\)=0.9780, x=2.3196, y=4.4292
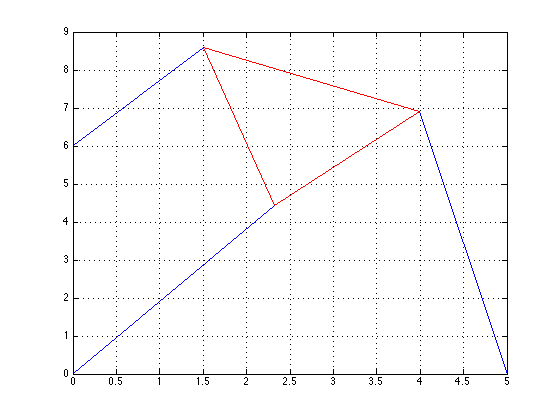
\(\theta\)=2.5128, x=3.2243, y=3.8216