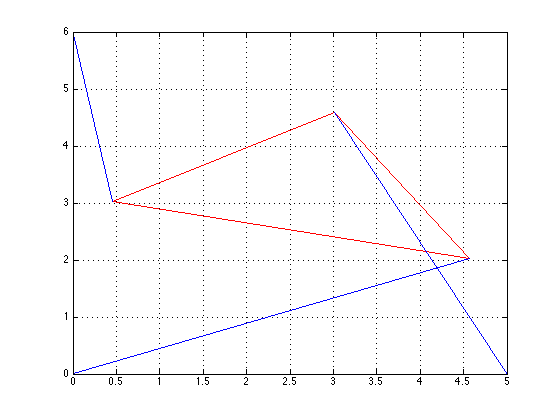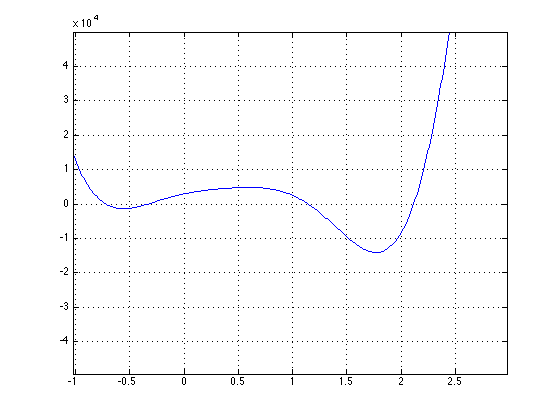
Part 4 asked us to solve the forward kinematics problem for the planar Stewart Platform specified by x1 = 5, (x2,y2) = (0,6), L1 = L3 = 3, L2= 3*sqrt(2), \(\gamma\) = pi/4, p1 = p2 = 5, p3=3. The first step was plotting f(theta) versus theta, to find where \(f(\theta)\) crossed the x-axis. The bisection method was then used to find the roots. The values of \(\theta\) which provided the zeros were: -0.7208, -0.3310, 1.1437, and 2.1159. Below is the plot for \(f(\theta)\) and then the four plots which show the four poses.

We then ran these theta values through the Project1xy.m script to get the x and y values of the first vertex, and the associated positions. A plot of each position can be seen below. The strut lengths were checked to make sure that p1=p2=5 and p3=3 using the vertices.m script, which gave the positions of the other two vertices in each triangle.
\(\theta\) = -0.7208, x=-1.3784, y=4.8062
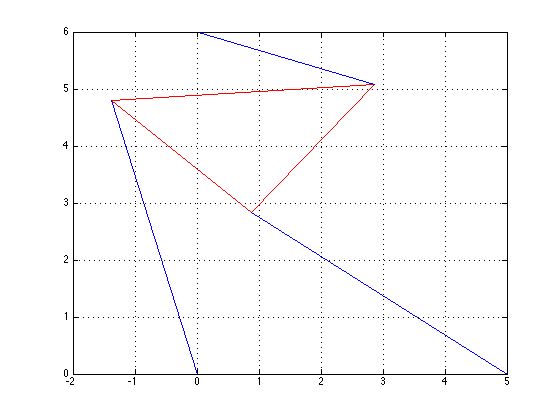
\(\theta\)=-0.3310, x=-0.9147, y=4.9156
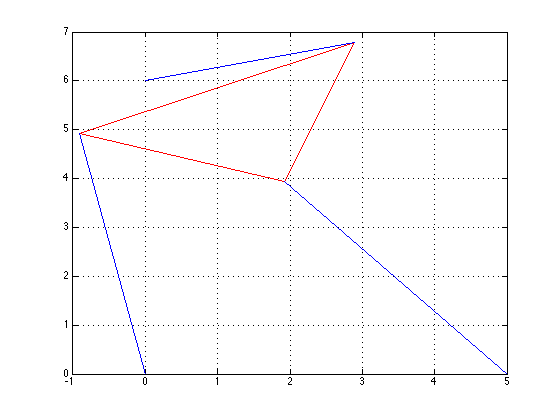
\(\theta\)=1.1437, x=4.4817, y=2.2167
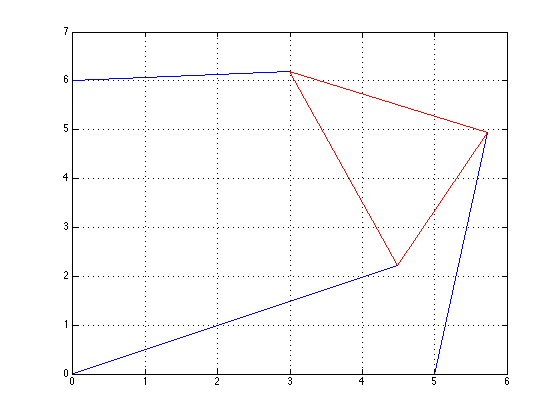
\(\theta\)=2.1159, x=4.5718, y=2.0244