Graphical Models: Assignment 2
Due February 5, 2019
- Answer the following true/false questions about the Bayesian network shown below. Explain your
reasoning.
- K is independent of A given F.
- F d-separates A from B and D.
- E is independent of H given B.
- B is independent of C given G and H.
- J is independent of D given E, H and C.
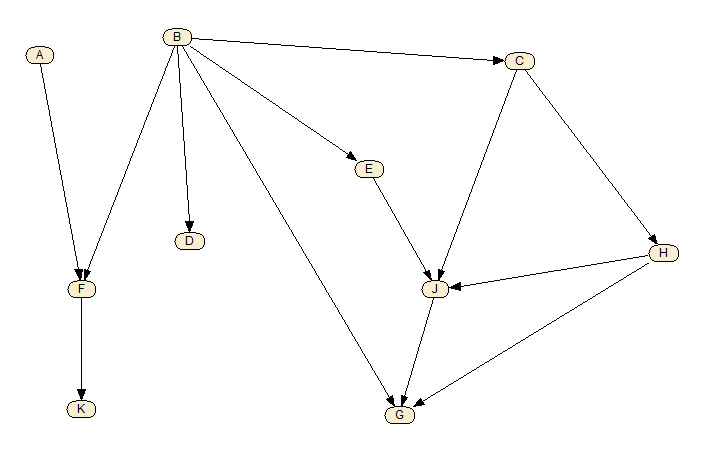
- Find the Markov blanket of F. Find the Markov blanket of E. Explain your reasoning.
- Assume each of these random variables has 5 possible
states. How many probabilities are needed to specify this Bayesian
network? How many probabilities are needed to specify a fully
general probability distribution on these random variables (i.e., 10
random variables, 5 states for each random variable)?
- Repeat Problem 3 if there are 10 states per random variable.
- Find a general formula for the number of probabilities needed to define a fully
specified joint distribution on n random variables with k states per
random variable? How many probabilities are needed for a Bayesian
network with n random variables with k states per
random variable if there is one root node, two nodes with one parent, and the rest of
the nodes with two parents? Compare the number of probabilities for a full distribution and Bayesian network for n=10 and k=5. Repeat for n=100 and k=10. Comment on your results.

