I propose to implement the Skipjack algorithm and Key Exchange Algorithms in C/C++ using some assembly code routines to optimize the encryption and decryption speeds. Then using this implementation I will compare the speed of the encryption and decryption for optimized DES implementations available. The Key Exchange Algorithm (KEA) will be implemented to be compatible with the FORTEZZA card.

The development will be conducted on a Pentium II using GNU C under Red Hat Linux 5.2. The initial implementation will not contain any assembly code routines to be portable across as many platforms as possible. The optimized implementation will only be compatible with Intel architectures. The standard C/C++ libraries should be sufficient for implementing the Skipjack encryption and decryption algorithms. In order to implement the KEA I will require a library to generate large prime numbers as well as large random numbers. This will also require operations on these large numbers for which I will use the SSLeay libraries. They contain header files and a binary library that can be linked with the final object file to provide functions to perform the above operations.

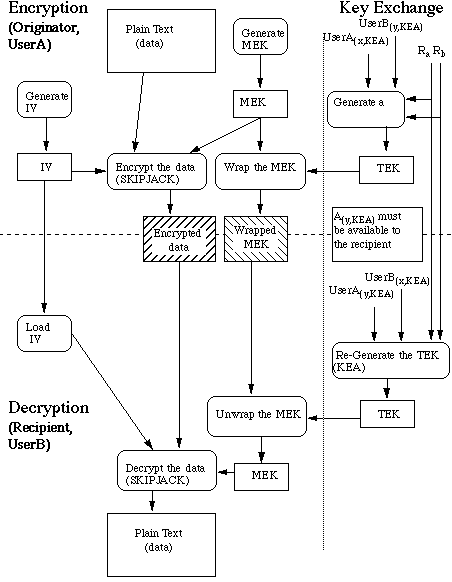
In order to send an encrypted file to another user it is necessary to have some way of exchanging the message encryption key used to encrypt the file with Skipjack. The key exchange algorithm for Skipjack uses a public/private key system in the encrypting of the secret key. A temporary encryption key is generated and used to encrypt the message encryption key for transmission to the receiver. In order to generate the temporary encryption key the recipient’s public key, the sender’s private key, and two random numbers are used. The two random numbers and the encrypted message encryption key, along with the encrypted message, are sent to the receiver. The receiver then uses the sender’s public key, their private key, and the two random numbers to recreate the temporary encryption key and decrypt the message encryption key. Figure 1 illustrates this transaction.

Assuming that each user has obtained the others public key through a secured and authenticated channel, then it is still necessary to transfer more than just the encrypted file to the other end. Along with the encrypted file the initialization vector, two random values, and encrypted message encryption key need to be sent. This information can be placed in a standard header and transmitted with the encrypted file. I am currently investigating if there is a standard format for this header.

Each user’s public cryptographic information is passed through a data structure known as a certificate. The FORTEZZA certificate structure is based on the certificates defined by the ITU-T X.509 Recommendation. Each FORTEZZA certificate contains, at a minimum, the user’s unique identifier and public key information bound by a cryptographic mechanism that can be authenticated. Its issuer then digitally signs the certificate using the Digital Signature Algorithm (DSA).

The Skipjack algorithm has four modes of operation, Output Feedback (OFB), Cipher Feedback (CFB), Codebook (CBE), and Cipher-Block Chaining (CBC), which are subsets of the FIPS-81 description of modes of operation for DES. This program will implement the CBC (used by the FORTEZZA card) and CBE modes of operation. To be compared with the speed for encryption and decryption with the equivalent DES modes.

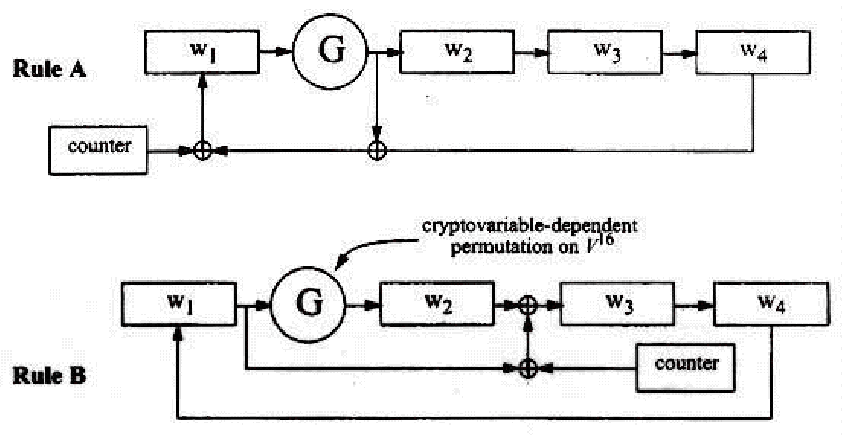
The Skipjack algorithm encrypts 64-bit data blocks by alternating between two stepping rules. Each stepping rule is similar in design, and is shown in Figure 1. Each of these steps is performed 16 times for a total of 32 steps. The cryptovariable–dependent (key-dependent) permutation G, which operates on 16-bit blocks of data, is a four round Feistel cipher, which utilizes a fixed byte-substitution table for F.

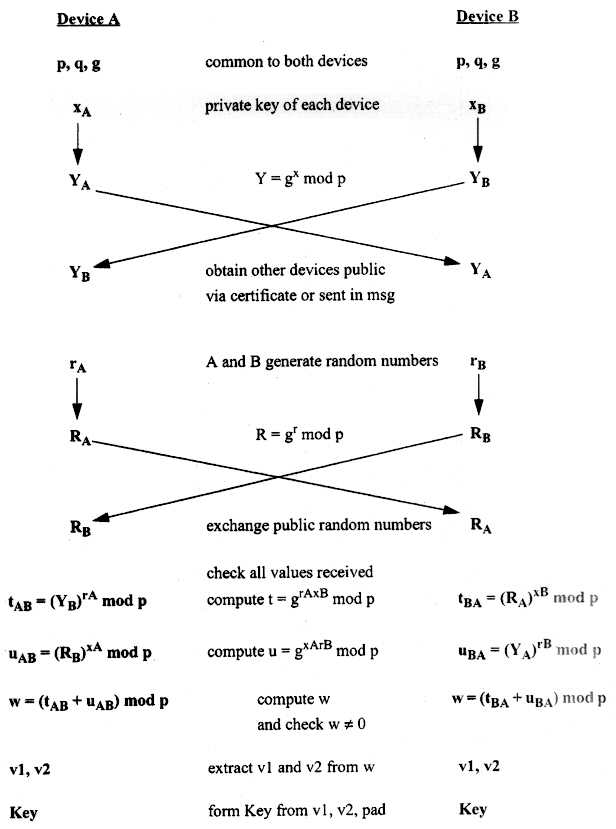
The KEA utilized three known parameters for each end sending the key, they are known as p, q, and g, with p and g being 1024-bit integers and q a 160-bit integer. Each device also has a 160-bit private key, x, which is converted to a 1024-bit public key and transferred to the other end. Then, a private 160-bit random number, r, is generated that is converted to a 1024-bit public random number and transferred between ends. Both of these public numbers are used to generate the proper key to be used for the Skipjack encryption. Figure 2 shows the KEA in detail.

 
To test the functionality of the program I will use the test vectors defined in the NIST Skipjack and KEA document. For testing the Skipjack algorithm in Codebook mode the following are used:

Plaintext input:  33221100 ddccbbaa

Cryptovariable: 00998877 66554433 2211

The output to each intermediate step will be compared to those listed in the document to ensure that each stage is correct. For the KEA there are also a set of defined test vectors. These are as follows:

P = 9d4c6e6d 42ea91c8 28d67d49 94a9f01b 8e5b5b73 0d0faae7 bd569dd1
    914e3ad4 759c8053 31eda145 9fb56be8 a8de4736 652a82b2 76e82acd
    63f5b78d 0b75a03e b34d397d be7b3740 8f72136a cb0879fe 61c718a3
    7f5154b5 078a7649 fb3d4fb4 c481e010 62c5241f 229fa580 423368dd
    51090dbf 25351f0c 5800de05 b92ba6a9

q = 97ad85fd 2b371ed0 69818ab3 c6ee8773 d9db029d

g = 595d3443 ec897c82 51e5fa9d 02ab8b75 c0fc57b0 969f880d a366a100
    01912a01 96bcb81c 41ac8485 031ac598 b5481eae 2726b719 d8dg915a
    6105973g 72386c0a 6a2c732c d6700d34 1f54bf28 d12d692d e2fa05f5
    5e898c2e 20bb8a26 02db1ba0 7de672e3 b96d9ac2 ga188450 63d918c3
    2ed71266 b783311a 0a8d08ac 487bea44

xa = 62319ac4 7de14518 0abd322c 59e2b600 2781e4g4

ra = 6201dd56 237c228a 3f54bc7e 794bdf32 41c67ea6

xb = 63decdad 4487eb71 31dff4fS 1cfbae39 446b9b3d

rb   =  52bfa1d7 2f1cf0fb 0ff6d5df 15fb7483 167eb0e7
 

To perform the performance comparisons between DES and this implementation of Skipjack the randomly generated files of varying sizes will be encrypted and decrypted. The time required to perform each will be compared and graphed.

By March 25^th I would like to have the Skipjack algorithm implemented without assembly code routines and verified as to its functionality. By April 8^th I hope to have the KEA and assembly code optimizations integrated with the implementation of Skipjack. By April 20^th I hope to have acquired an optimized implementation of DES and performed the comparisons and benchmarks for DES versus Skipjack.

I do not foresee any changes occurring as the project progresses.