Math 447 Project 5: A Simple Audio Codec

In this project, Audio Compression is investigated. In addition to those topics, an introduction to Information Theory was given as well. To begin, one began by breaking a signal, be it an image or audio, into it's frequency components. In this project, the Discrete Cosine Transform (DCT) was used. The Discrete Cosine Transform is related to the Discrete Fourier Transform (DFT). The difference between the DCT and the DFT is that the DCT operates on purely real data with even with even symmetry. One might wonder if a Discrete Sine Transform (DST) exists. It turns out that it does, and the DST is used for real data with odd symmetry. The one-dimensional DCT is n by n matrix given by the following:

for i,j = 0...n-1, where

if i=0

or

1 if i = 1,...,n-1

In the same manner one uses the DFT to change to the Fourier Basis, one uses the DCT. The components of the output of the DCT are the magnitudes of the frequency components of a signal. One can also consider the ubiquitous perspective of projections. Each Fourier Coefficient represents the magnitude of the projection onto the basis element.

The DCT is used for image compression. In the case of audio however, the Modified Discrete Cosine Transform (MDCT) is used. It is given by the following:

The major difference between the DCT and the MDCT is that MDCT is a n x 2n matrix. This would seem to cause problems with invertibility. After all, what good is a transform if one cannot go back to where they came from? To get around this, one overlaps the vectors. Through overlapping of two vectors, one gets a square matrix.

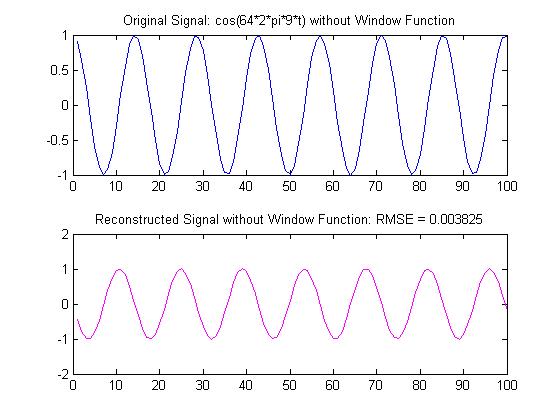
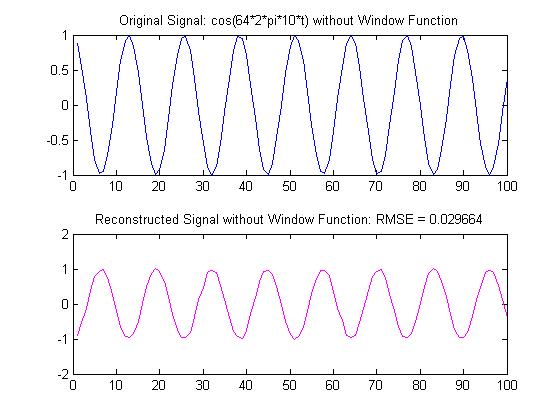
1. The first task in the project was to investigate the output of the MDCT for even and off integer values of f. The signal used was a pure cosine of f * 64 Hz. The value of f would multiply 64 Hz by an integer value. An interesting pattern emerged for even and odd integer values of f. When f was even, the MDCT output would have almost entirely zero entries. The tone could be reconstructed without noticeable distortion with only 4 bits. However, when f was even, almost every entry of the output had a value of some kind. After quantization and de-quanitization, the output could not be fully reconstructed without distortion with 4 bits. With 8 bits however, one was able to achieve a better reconstruction of the signal. Plots of an odd and even value of the Codec are given below. These plots represent a small portion of the signals:

Note: The graphs are not in alignment due to the nature of the MDCT. The audio signal is compressed by taking overlapping chunks of the original and putting them back together at the end. The shift occurs because one cannot take an overlapping segment of the first 32 samples unless they used zero padding which was not discussed in this project.

Of course, one might wonder why this happens? It is due to the nature of the MDCT itself. The ith row (i=0,1,...2n-1) of the MDCT is given by:

In the case of this Project, with a sampling rate of 8192, the vector of cosine is:

Now, when j spans from 1 to 2n, one will get a half period of the cosine wave they are transforming to the frequency domain. Since this signal is already present in the transformation itself, one does not need any frequency contributions elsewhere. However, when f is even, the convenience of the odd values of f is not present anymore. Now, that signal requires multiple frequency components to be represented in the frequency domain. This also explains why less bits were needed with the odd values of f. When f was even, more of the so-called Fourier Coefficients were being quantized, and the quantization of multiple Fourier Coefficients had a detrimental effect on the signal reconstruction.

Code Here

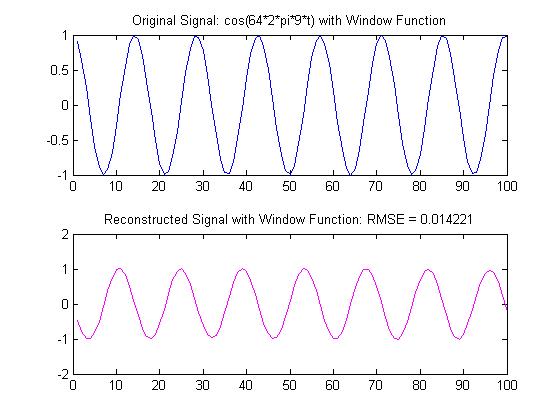
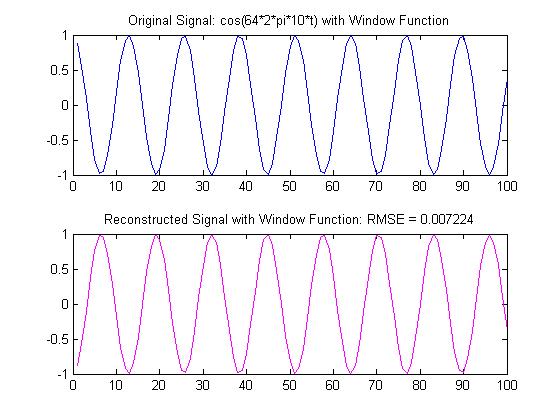
2. Next, a window function was added to aid in smoothing the overlapping windows of the output signal. The window function is given by the following:

To gain a literal insight of how this was implemented, the best recourse is to view the code, given below. The comments should provide ample insight into the implemenation.

With the window function, even signals could be purely reconstructed using only 4 bits in the quantization step. This represents an improvement over the results in Step 1. Plots of the signals shown in problem one are shown here with the Window Function:

Code Here

3. Next, a major chord was implemented into the Coder, and the RMSE between the original signal and the compressed signal was calculated. As the number of bits was increased, it was found that the RMSE would slightly decrease. Oddly enough, 5 bits turned out to have the smallest RMSE. The following results were recorded with a major chord containing 576 Hz, 720 Hz, and 826 Hz:

4 Bits: RMSE = .0158

5 Bits: RMSE = .0087

6 Bits: RMSE = .0044

7 Bits: RMSE = .0024

8 Bits: RMSE = .0014

9 Bits: RMSE = .0007

10 Bits: RMSE = .0003

16 Bits: RMSE = .000006

32 Bits: RMSE = .00000000009

64 Bits: RMSE = .000000000000001

4. In part four, a music video was made featuring different compression of Heavy Shift's "The Last Picture Show." Heavy Shift is a British Acid Jazz trio featuring Willie South (Piano), John Wallace (Saxophone), and Julian Fenton (Drums). Their debut album, Unchain Your Mind, featured the song "90 Degrees in the Shade," which reached the top five on the new adult contemporary charts in 1995. Additionally, it was voted "Album of the Year" by Jazz FM and dubbed "a soundtrack for the post acid 90's." Their second album, "The Last Picture Show," is described by the artists as:

"Pouring a heady cocktail of hip-hop beats, cutting edge jazz fusion and heart moving R&B into a decadently large glass, topped up with a dash of drum 'n' bass and liberal sprinkling of swing, the album is an intelligent and innovative collection of atmoshpheric tracks."

This video features six different compressions of Heavy Shift's "The Last Picture Show." They are listed below and marked in the video:

I. Original Version

II. 7 Bit Compression with Window Function

III. 8 Bit Compression with Window Function

IV. 4 Bit Compression with Window Function

V. 8 Bit Compression no Window Function

VI. 9 Bit Compression with Window Function

The scenes in the video are from Mark Eteson's Aventus (Temple One Remix) Music Video.

An intersting result of the compression is that the size of the .wav was reduced considerably without any noticeable degredation in quality, Case IV withstanding. The compression file size results are given below:

I. Original Version: Same

II. 7 Bit Compression with Window Function: 8,528 KB to 4,264 KB

III. 8 Bit Compression with Window Function: 4,393 KB to 2,197 KB

IV. 4 Bit Compression with Window Function: 4,221 KB to 2,111 KB (Noticeable loss of quality)

V. 8 Bit Compression no Window Function: 8,355 KB to 4,178 KB

VI. 9 Bit Compression with Window Function: 6,977 KB to 3,489 KB

The video is given below:

This project was both fascinating and rewarding! I thoroughly enjoy the study of Fourier subjects, and to top it off, this project had great applications as well. As with every reality check studied during the semester, the project is only the tip of the iceburg. I will say that given my study of Fourier subjects and filtering in Electrical Engineering, the subject of audio and image compression, as well as Huffman Coding, are subjects I sincerely hope I can study more during my time here at GMU. The practicality of audio and image compression in today's society goes without saying. One way or another, virtually everyone in some way shape or form encounters this subject. Whether it is someone putting songs on their MP3 player, or someone sending drunken pictures from their phone at 3:00 AM, the subjects of compression and Information Theory effect those individuals. I would most certainly spend an entire semester studying these subjects if I could.

References

Sauer, T. Numerical Analysis 2nd Ed. Pearson

Image courtesy of http://www.amazon.com/gp/customer-media/product-gallery/B000003MWX/ref=cm_ciu_pdp_images_0?ie=UTF8&index=0