Rotating Stewart Platform. Digital image. Wikipedia. N.p., n.d. Web. 04 Feb. 2014.
http://upload.wikimedia.org/wikipedia/commons/a/a7/Hexapod_general_Anim.gif.
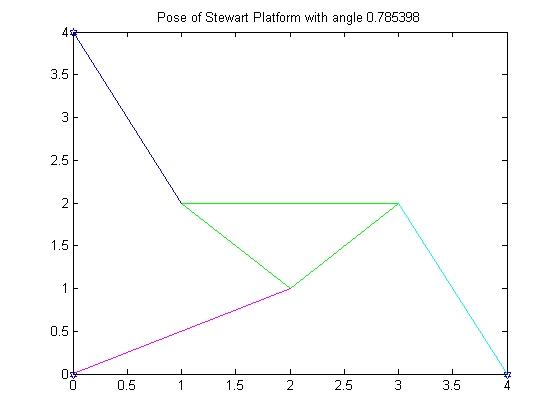
As seen above, the Stewart Platform consists of six struts of variable length. These struts can rotate to support various payloads. These payloads include applications in flight simulation, carnival rides, and surgical procedures. In our setting, the Stewart Platform was simplified to a 2-Dimensional version with three struts. In this 2-Dimensional setting, the platform is rotated about an angle, theta, and is supported by three struts of variable lengths. In this project we had to solve for valid poses of the platform, given various initial conditions. In order to solve for the valid poses, the Bisection Method was implemented.
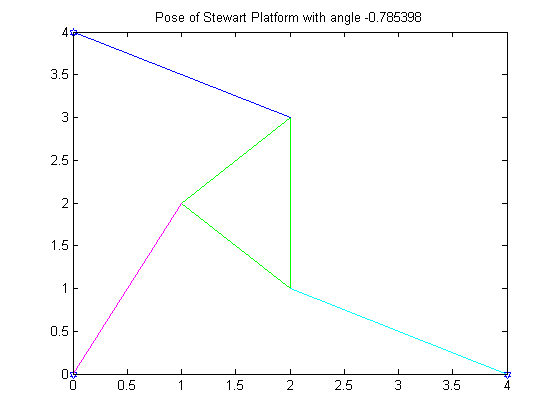
1. To begin with, we wrote our function with the initial conditions specified in Problem 1. The graphs below show the position of the Stewart Platform at angles of pi/4 and -pi/4. These angles represent the two roots of the equation with the given initial conditions. The Bisection Method was used to find the two roots of the equation.

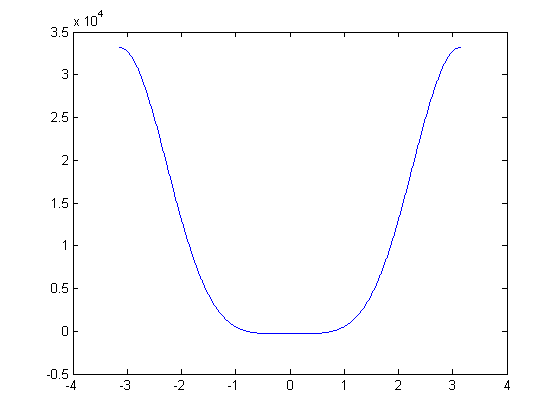
2. Next, to gain a further intuition for the position of the roots of the function, we plotted the Stewart Platform function on the interval of [-pi,pi]
3. (The two poses of the Stewart Platform with roots at pi/4 and -pi/4 were shown previously)
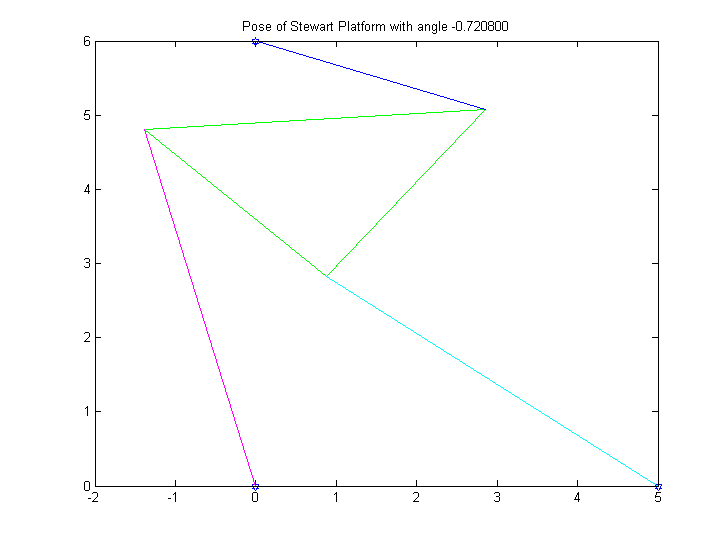
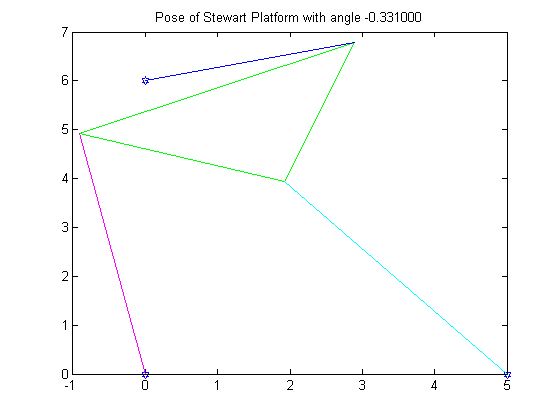
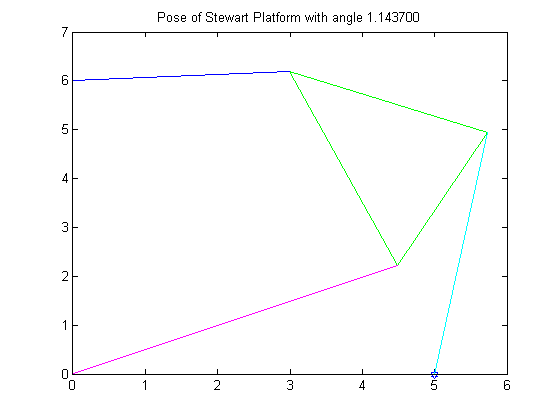
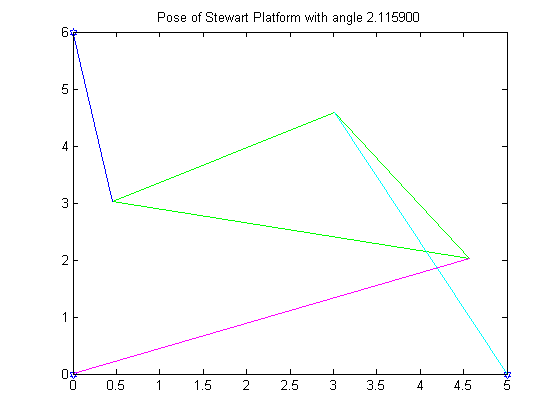
4. Next, we were given a new set of initial conditions. This time around however, we did not know the angles that satisfied the poses of the Stewart Platform. Using the Bisection Method with a tolerance of .0005 we were able to find the following roots of the equation:
R1 = -.7208
R2 = -.3310
R3 = 1.1437
R4 = 2.1169
The First Graph shows the graph of the function.
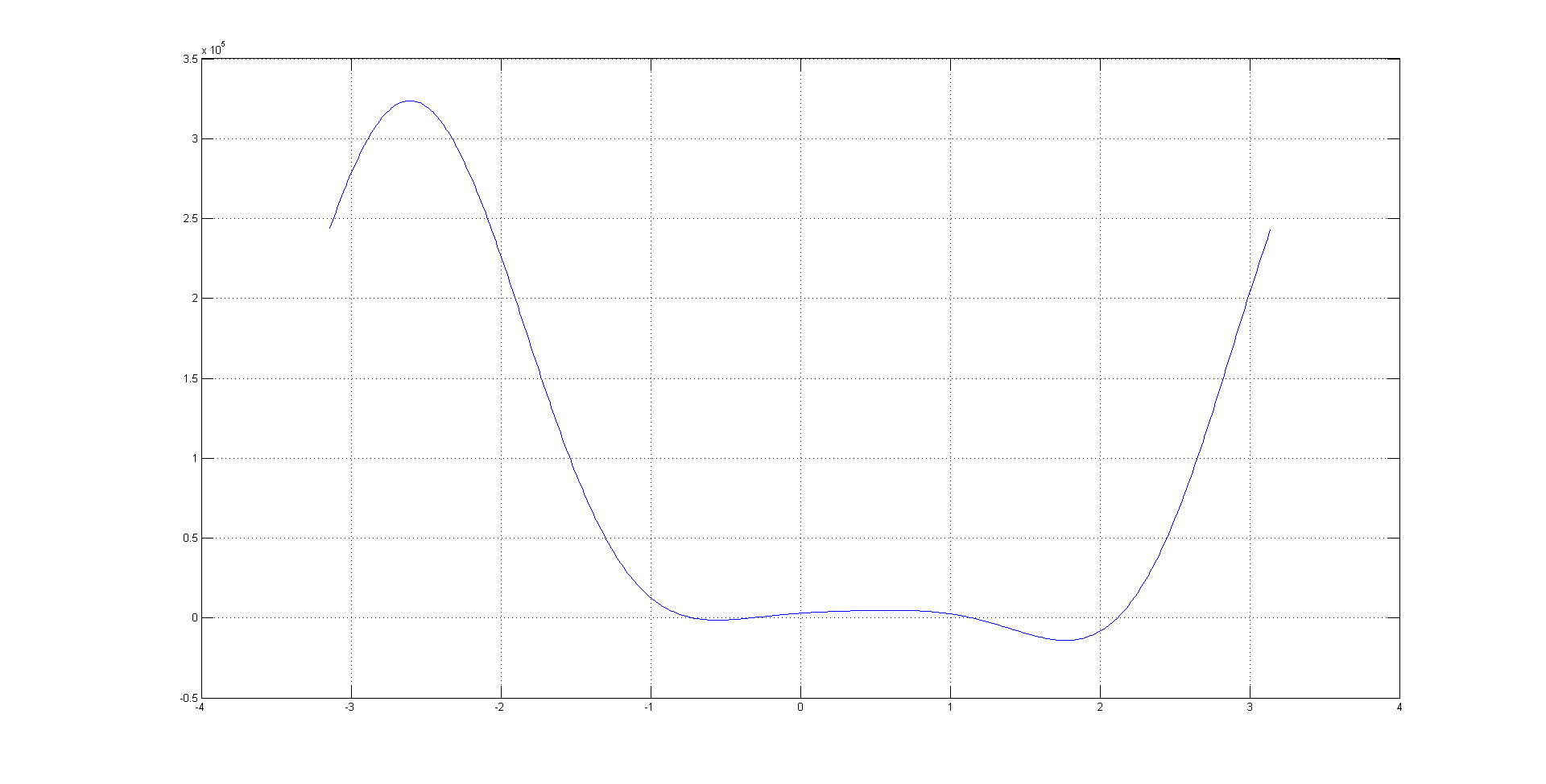
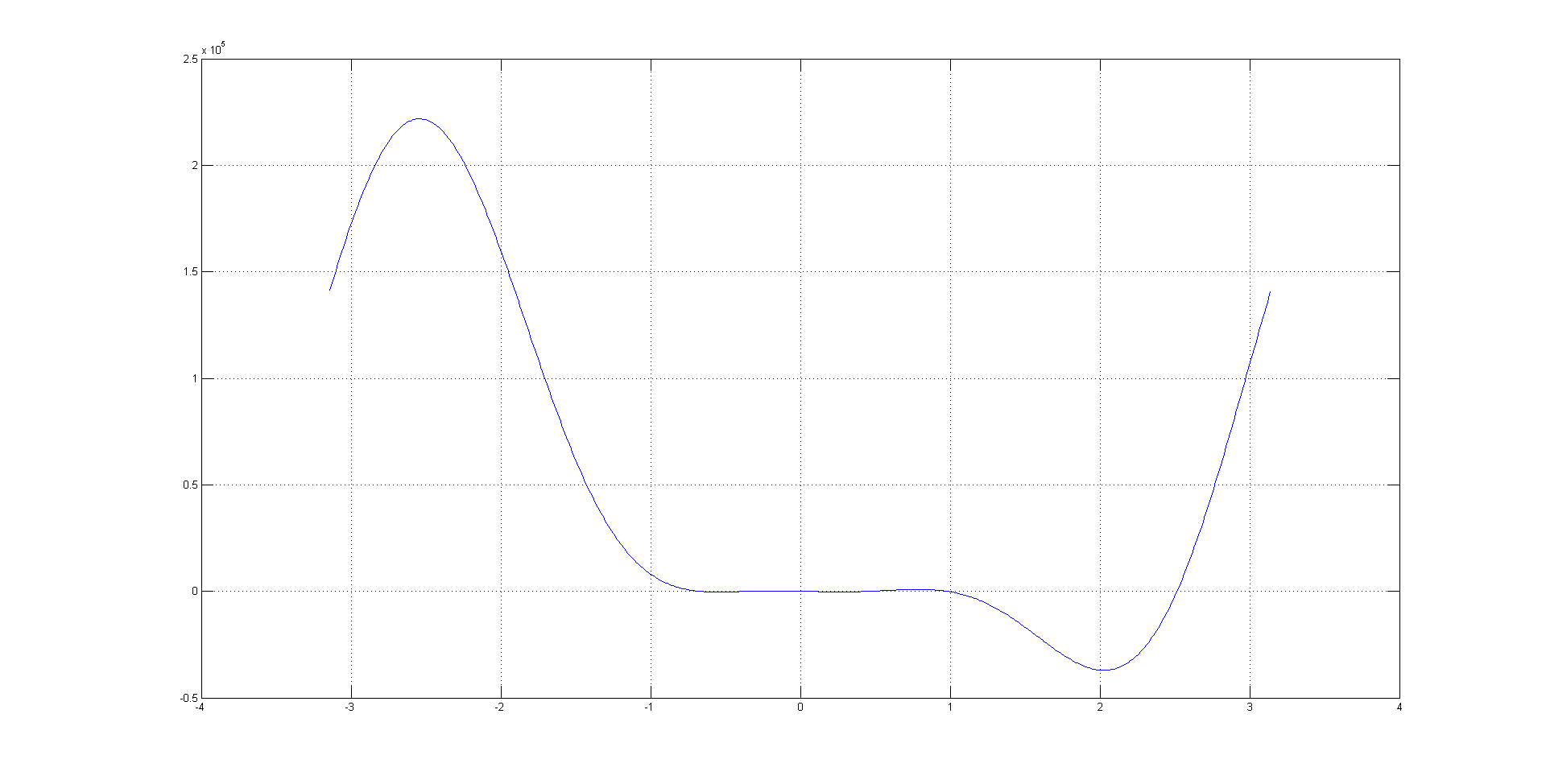
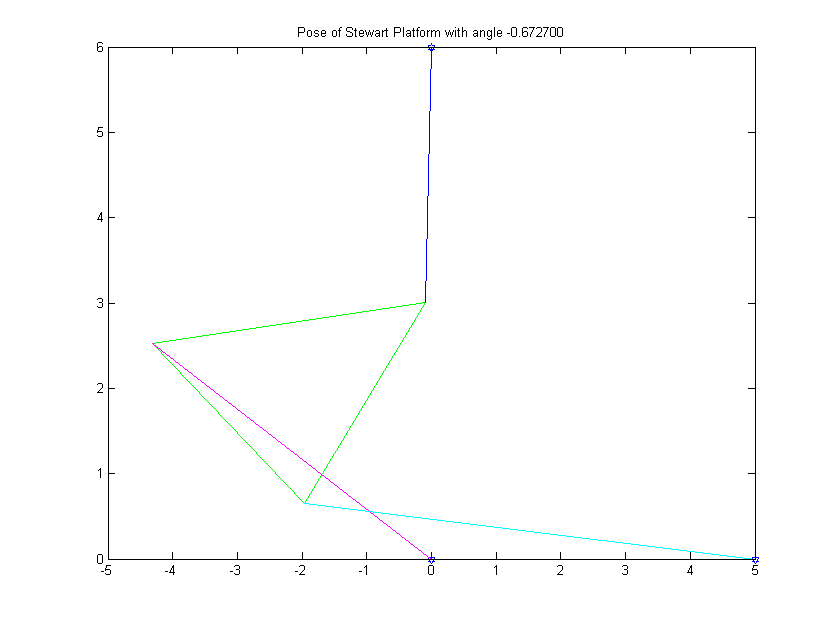
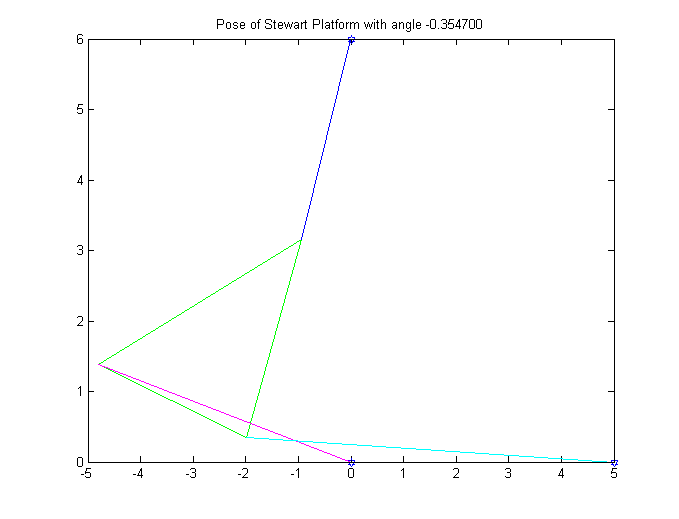
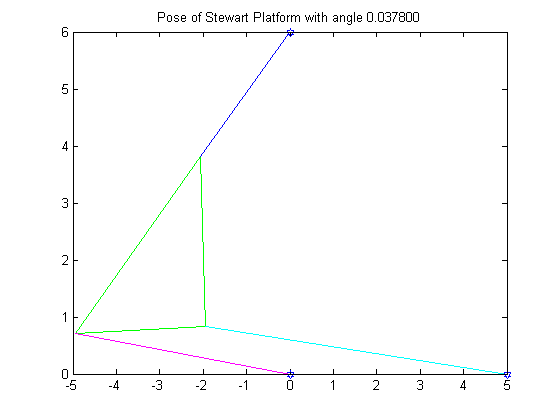
5. In this problem, the length of one of the struts, p2, was changed to 7. As a result, there are now six roots to be solved for. Once again, we used the Bisection Method and found the following roots:
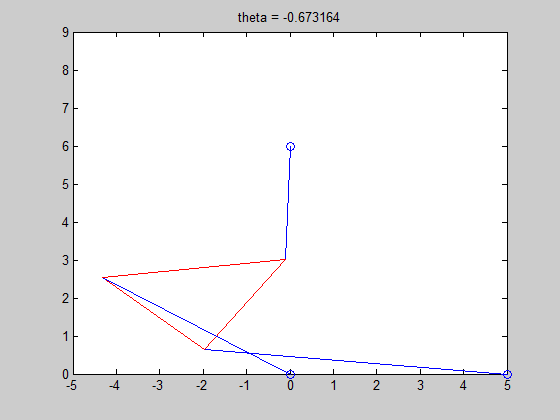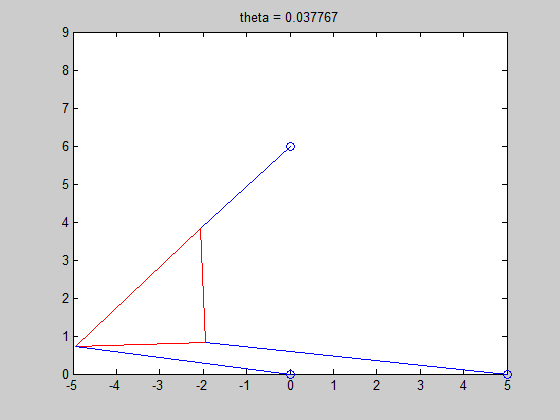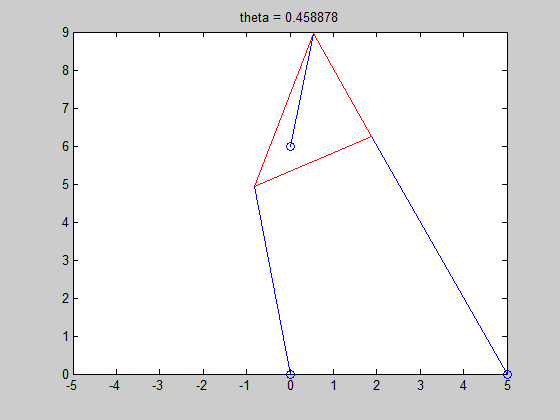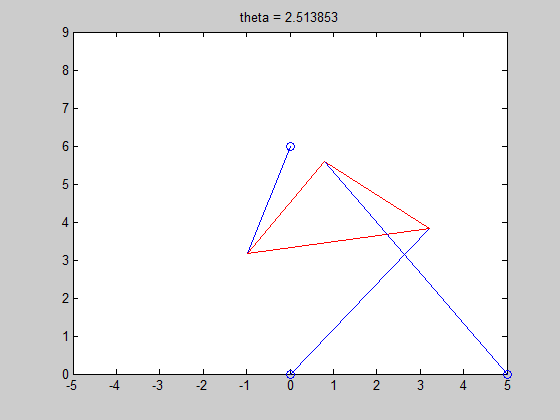
R1 = -.6727
R2 = -.3547
R3 = .0378
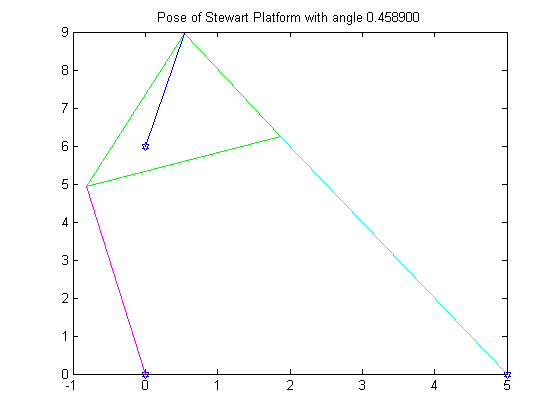
R4 = .4589
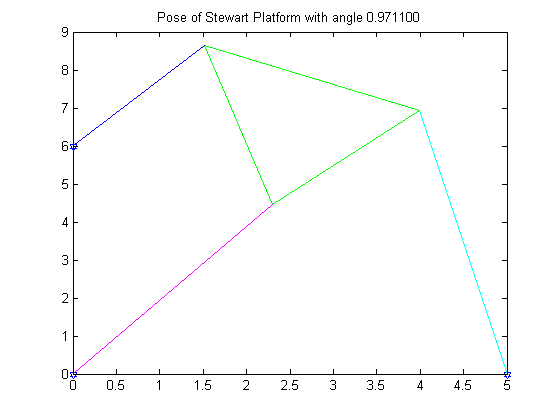
R5 = ,9711
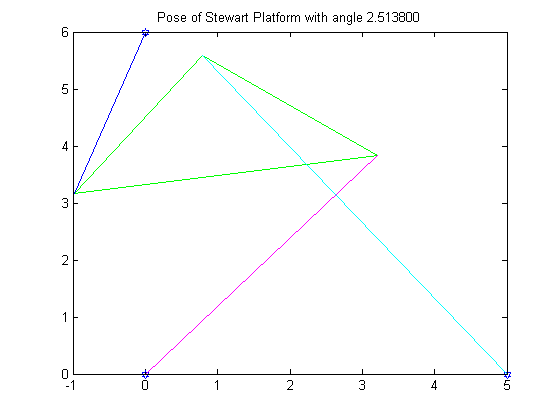
R6 = 2.5138
Like in the previous problem, the first graph shows the graph of the function. The last graph is an animation of all six poses.
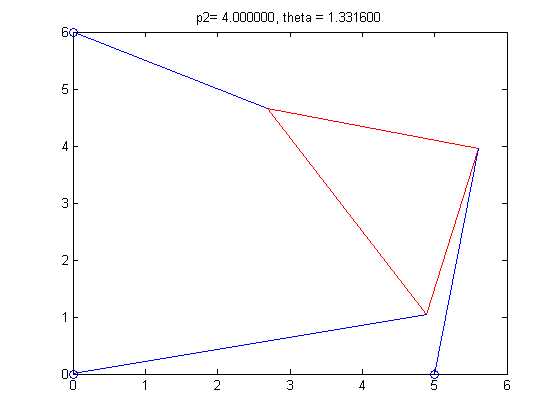
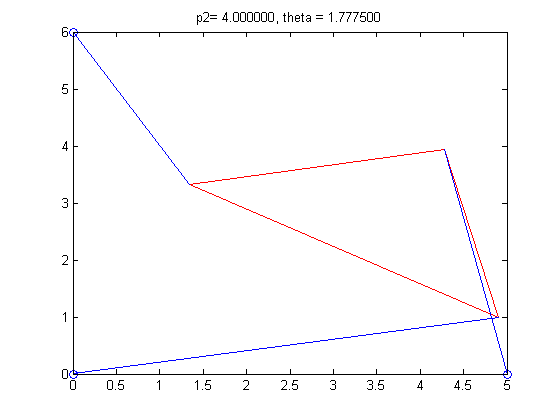
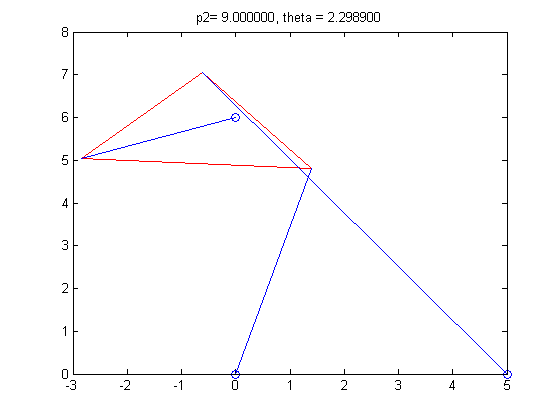
6. For the last part of the project, we had to find a length for strut p2, that resulted in the Stewart Platform only have two poses. Simple trial and error yielded a length of 4. We also constructed an animation of poses with ascending lengths for strut p2, and determined the number of roots in each pose.
Roots graph:
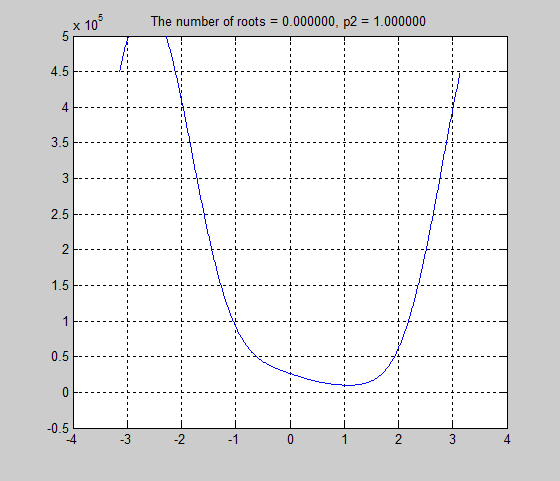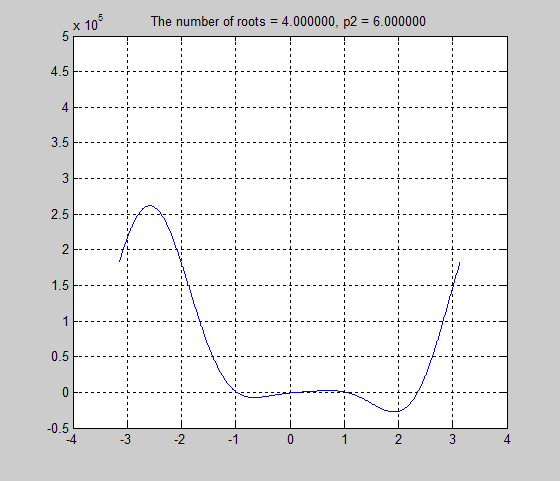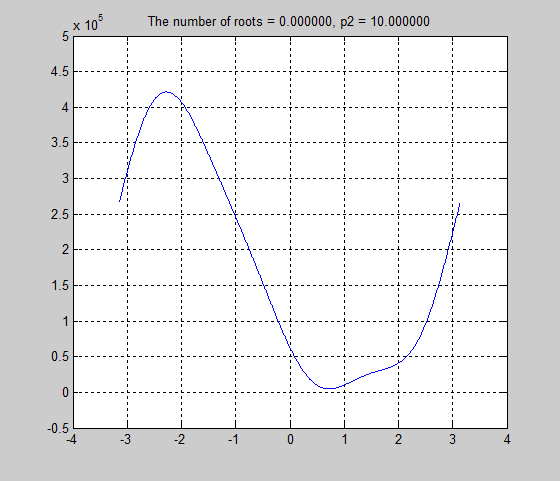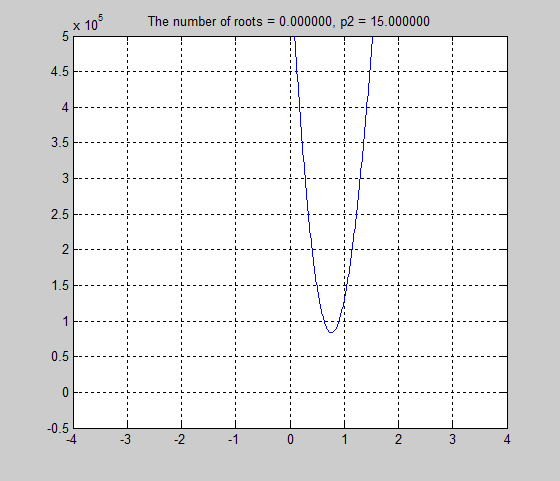
p2=4
theta = 1.3316, 1.7775
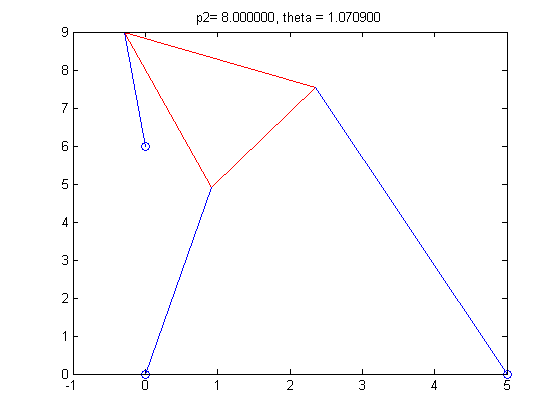
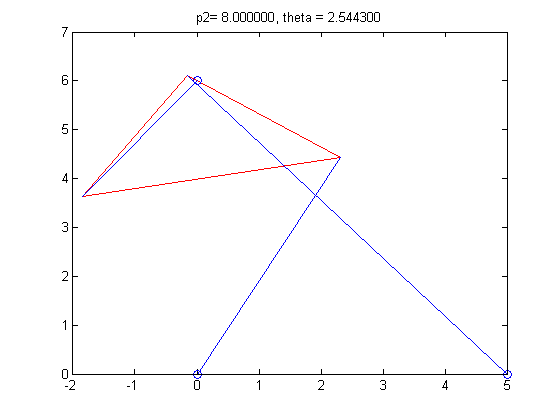
p2=8
theta = 1.3316, 1.7775
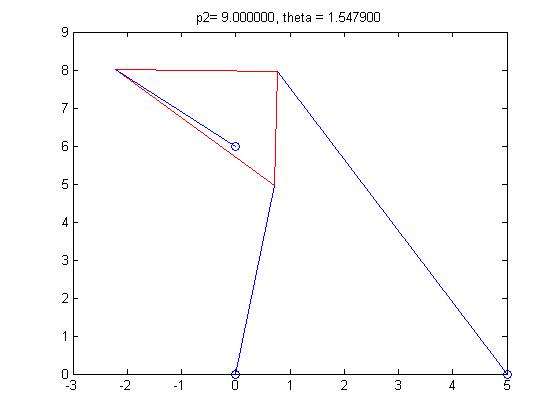
p2=9
theta = 1.3316, 1.7775
This project was a very enjoyable collaboration. Our individual abilities complemented each other very well. Much of the time, the problems were solved collectively, with plenty of discussion between the two of us. The first moving graph was coded by Wonjun himself. The other moving graph was brainstormed by the two of us, and was coded by Wonjun as well. This was agreed upon by the two of us, as I (James), was responsible for typing the Project summary and verifying that the norms were correct in Problem 4.
Sauer, T. Numerical Analysis 2nd ed. Pearson