For the fifth problem, add the ability to use different levels of bit quantization for different frequencies: in essence, to change the value of \(b\) in order to provide better precision where it will be most noticeable.

To do this, I used a modified version of the D'Hondt (Jefferson) method, a method for allocating seats in a proportional voting system. First the bit array is initialized to some minimum precision level - I chose 2 bits. Next, the MDCT is quickly run along the length of the audio file and the averages of all \(y_k\)s are recorded. Now, for each bit of precision that we wish to allocate (I wished to have an average 6 bits per value so this process was repeated \(4n\) times), we find \(\frac{\overline{y}_k}{(b_k+1)^4}\) for all \(k\) and add a bit of precision to the coefficient for which this value is the highest. (The original method does not raise the denominator to the fourth power - I added this to account for the vast differences in order of magnitude between coefficients). To prevent one coefficient from hogging all the precision, I set a hard cap of 8 bits.

Relevant files: prob5codec.m, question5a.m, and prob5a.txt.

b = 3, RMSE = 0.0028	b = 4, RMSE = 0.0013
b = 5, RMSE = 0.0009	b = 6, RMSE = 0.0007

The importance sampling shows significant improvement over simple quantization. Comparing the results of prob2codec and prob5codec shows the decrease in RMSE:

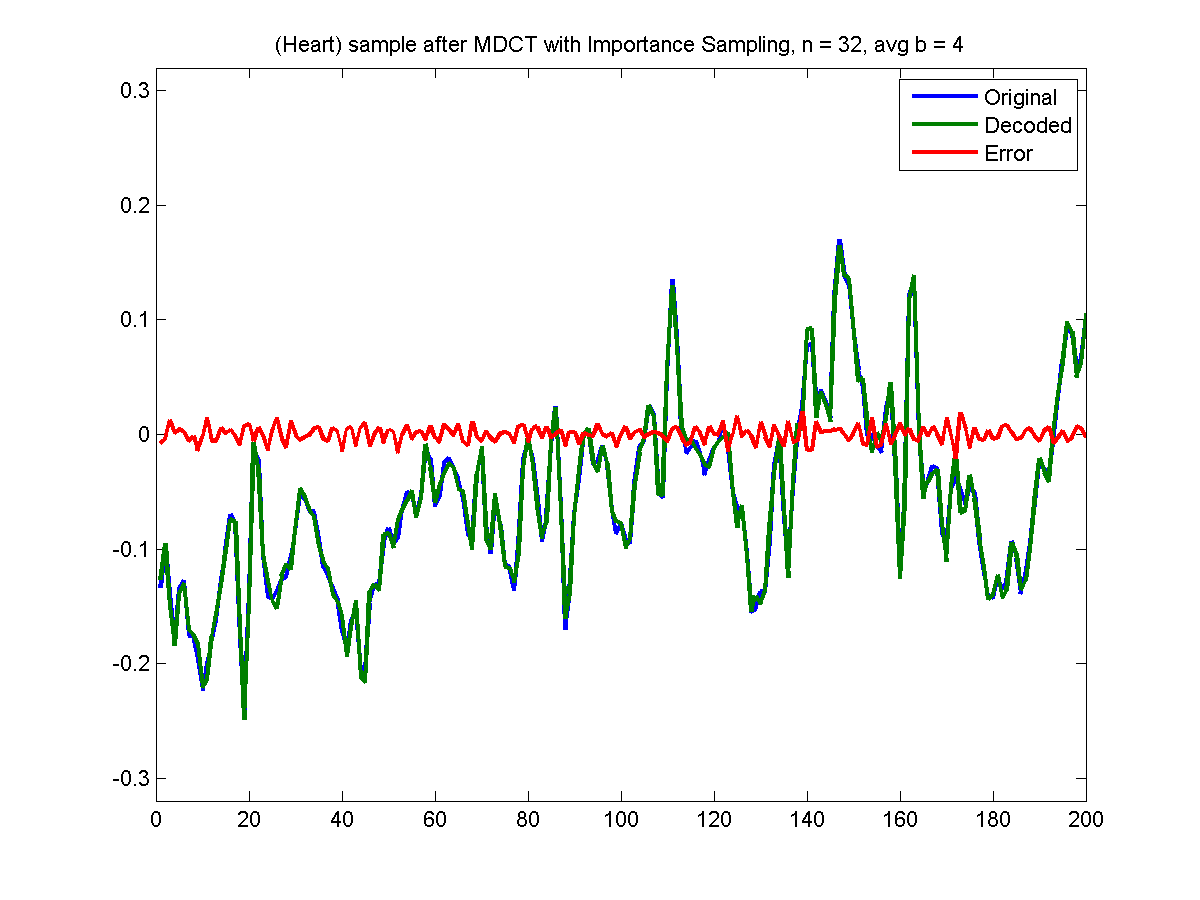
Let's try compressing the same ♥ (Heart) sample from part 4:

b = 4, RMSE = 0.0060

  Original:
Decoded:
      Error: