For this assignment, I looked at several variants of the Discrete Cosine Transform (DCT), a process by which sequences of numbers are converted into amplitudes of cosine functions at various frequences, which can be recombined in order to generate the original points. More specifically, the DCT of a set of \( n \) points, \( x \), can be found by generating the \( n \times n \) matrix below, \( C \), and multiplying to get \( y = Cx \). Because \( C \) is a real orthogonal matrix, its transpose is its inverse, meaning you can reverse the process by calculating \( x = C^T y \).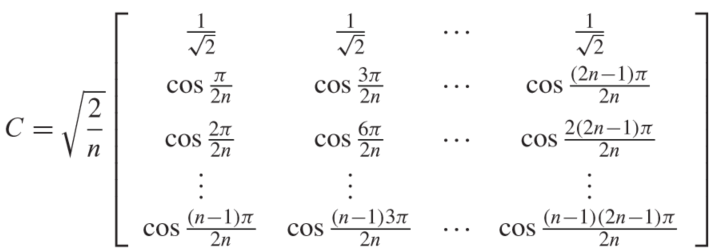

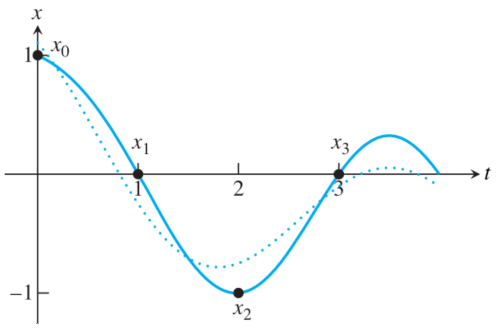
Left: the DCT transformation matrix. Right: DCT interpolation of four points, with (solid line) and without (dotted line) the fourth coefficient.

The DCT is commonly used in image and audio compression due to its resilience to information loss for gradually changing signal data: individual \( y_i \)s can be discretized to fit into an arbitrary number of bits, and higher-frequency \( y_i \)s can be dropped entirely, without significantly compromising the overall structure of the data (as shown above).

For my project, I investigated the Modified Discrete Cosine Transform (MDCT), in which an \( n \times 2n \) matrix M is used to generate "layered" transforms, in which each length-\(n\) window is decoded by overlapping two length-\(2n\) vectors, a technique which is designed to "smooth" any discontinuities between windows, preventing recurring distortion along window edges.