For this assignment, we sought to approximate solutions \(u(x,y)\) to partial differential equations of the form \[ u_{xx} + u_{yy} = f(x,y), \] also known as Poisson equations, on two-dimensional rectangular domains with various boundary conditions: Dirichlet boundary conditions, which fix the value of \(u\) on the boundary, Neumann boundary conditions, which fix the first derivative, and Robin boundary conditions, where the first derivative and value are a function of one another.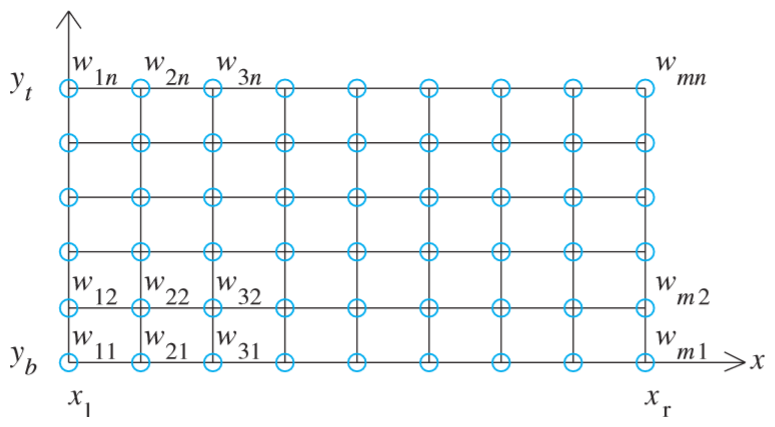

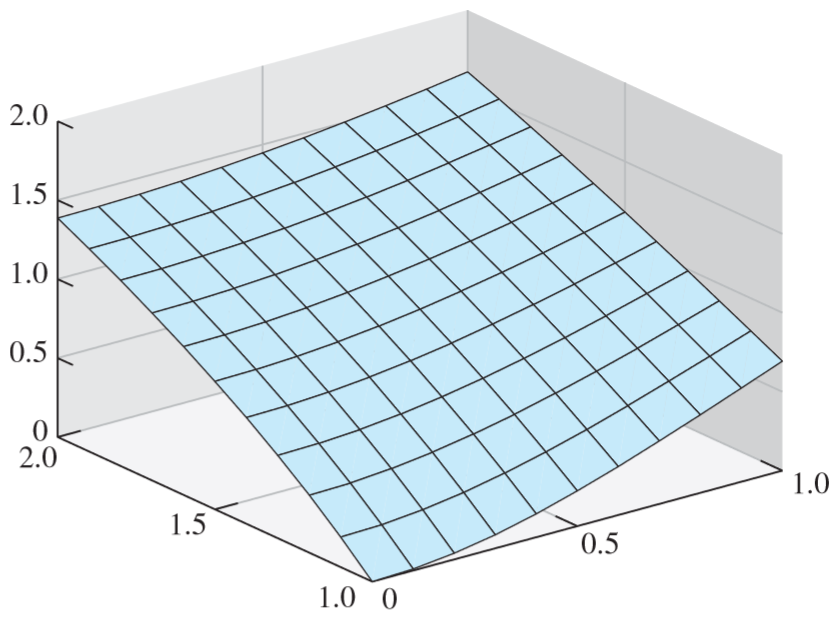
Left: rectangular x,y domain discretized into grid squares. Right: example mesh plot of calculated \(w\) values.

This is done using the Finite Difference Method, discretizing the domain into an \(M \times N\) grid, each grid square having dimensions \(h \times k\) (see above left), and then constructing a system of linear equations using the second-order finite difference equation \[ \frac{w_{i-1,j}-2w_{i,j}+w_{i+1,j}}{h^2} + \frac{w_{i,j-1}-2w_{i,j}+w_{i,j+1}}{k^2} = f(x_i, y_i) \] for all interior points, and application-specific boundary equations for all others. This system can then be solved for \(w(x,y) \approx u(x,y)\) on the grid (see above right).

In the following pages we will show two example applications of this method: using Robin boundary conditions to simulate convection and conduction of heat in a cooling fin, and solving the Laplace equation with discontinuous Dirichlet boundary conditions.