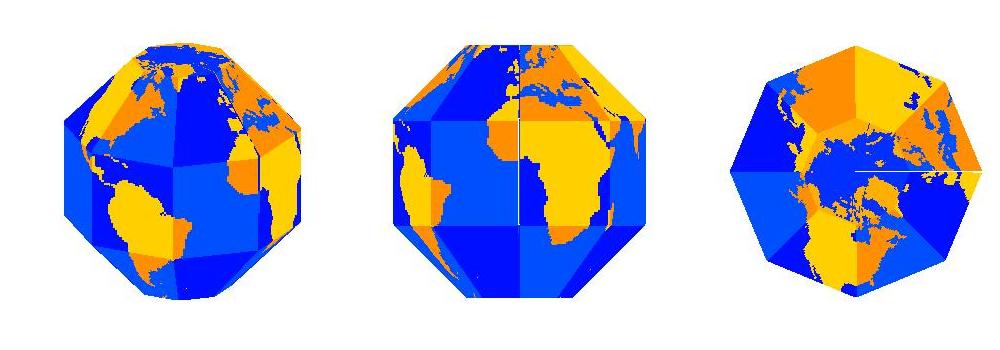
Illustration of Octaglobe Sector Globe; colors show faces of polyhedron and location of land and sea.

Illustration of Octaglobe Sector Globe; colors show
faces of polyhedron and location of land and sea.
A Sector Globe is a polyhedron used to approximate a sphere in order to represent features on the Earth or some other sphere. It can easily be constructed from a print-out using scissors and tape. Most of the faces of the polyhedron are squares or trapezoids, and the polar caps are represented by a polygon centered on each pole. Each face represents a sector of the globe bounded by latitude circles and longitude circles (except the polar faces, which are bounded by a single latitude circle). In this way, there is a simple and intuitive relationship between location on the Sector Globe and its latitude-longitude coordinates on the Earth. Each longitude circle on the Earth is represented by a regular polygon (for instance the outline of the middle figure in the illustration above). Each latitude circle is represented by a regular polygon of the same shape as for longitude (see right figure in illustration). Longitude is proportional to the distance along the longitude polygons and latitude is proportional to distance along the latitude polygons.
The illustration shows an Octaglobe, which uses octagons to represent latitude and longitude. Each tropical and midlatitude face of the Octaglobe represents a 45o X 45o sector. Octagons represent the polar caps. Since the tropical sectors straddle the equator, they reach from 22.5o S to 22.5o N. Similarly, the midlatitude sectors reach from 22.5o to 67.5o. By coincidence, the tilt of the earth is about 23.5o, so that the Tropics of Cancer and Capricorn (at about 23.5o in each hemisphere) and the Arctic and Antarctic circles (at about 66.5o) are close to the sector boundaries.
The Octaglobe is a good compromise between accuracy and convenience. There are few enough faces that it can be constructed by cutting, folding, and taping a flat image in about 20 minutes. There are enough faces that the distortions to a sphere are relatively small. The Octaglobe is obviously significantly different from a sphere, but it represents areas and distances on a sphere pretty well.
A Dodecaglobe, based on dodecagons in latitude and longitude and faces representing 30 X 30 degree sectors, gives a highly accurate approximation to a sphere. However, its greater complexity makes it take about twice as long to construct as an Octaglobe. Some other people have created cubic globes, but these introduce pretty significant distortion into the map.
Last modified: 28 June 2012