Introduction
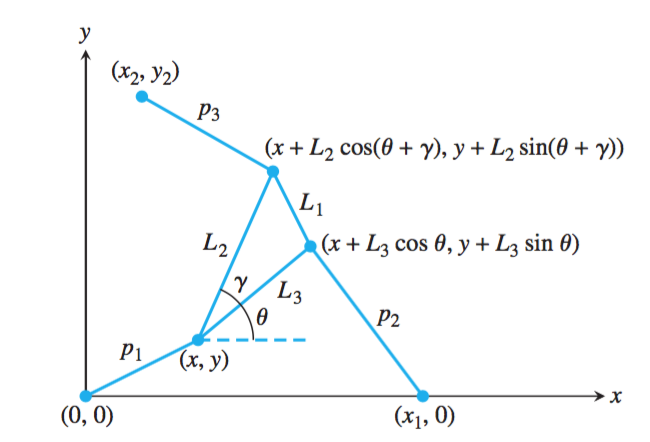
The stewart platform is a three dimensional platform with 6 degrees of freedom, or rather 6 strut lengths which control the orientations of the platform. In this project, we explore a two-dimensional analog: a triangular platform controlled by 3 struts, which are anchored to three points (\(0,0), (x_1,0)\), and (\(x_2,y_2)\)
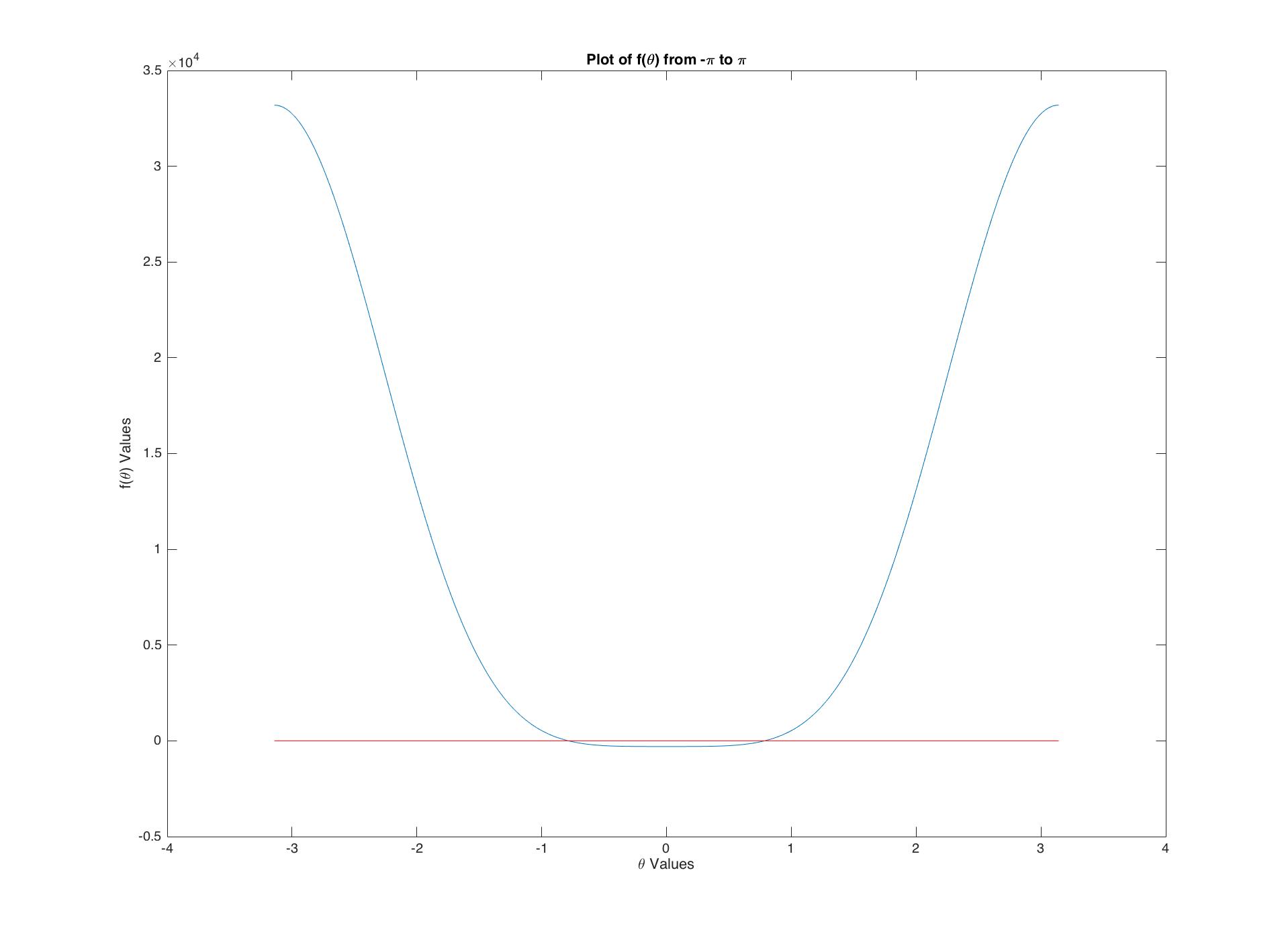
In this project, we examined the geometry of the 2D Stewart Platform in order to solve its forward kinematics, or rather the orientation of our platform given the individual strut lengths, and \(\gamma\). Our Matlab code creates a function in terms of a single variable \(\theta\), whose zeros correspond to different orientaions of the triangle.
From simple trigonometry, we obtain that $$ p_1^2 = x^2 + y^2 $$ $$p_2^2 = (x+ A_2)^2 + (y+ B_2)^2$$ $$ p_3^2 = (x+A_3)^2 + (y+B_3)^2$$
where
$$A_2 = L_3cos(\theta) - x_1 $$ $$B_2 = L_3sin(\theta)$$ $$A_3 = L_2cos(\theta + \gamma) - x_2 $$ $$B_3 = L_2sin(\theta +\gamma) - y_2$$
These equations provide a solution to the inverse kinematics problem. Given an angle \(\theta\), and position \((x,y)\), we can calculate the corresponding strut lengths for the platform. The forward kinematics problem, however, is more complex
We can solve the forward kinematics by eliminating \(x\) and \(y\).
We set $$ x = \frac{N_1}{D} = \frac{B_3(p_2^2 - p_1^2 - A_)2^2 - B_2^2) - B_2(p_3^2 - p_1^2 - A_3^2 - B_3^2)}{2(A_2B_3 - B_2A_3)}$$ $$ y = \frac{N_2}{D} = \frac{-A_3(p_2^2 - p_1^2 - A_2^2 - B_2^2) + A_2(p_3^2 - p_1^2 - A_3^2 - B_3^2)}{2(A_2B_3 - B_2A_3)}$$
Substituting back into the first equation, we get a single equation in the variable \(\theta\), $$f = N_1^2 + N_2^2 - p_1^2D^2 = 0. $$