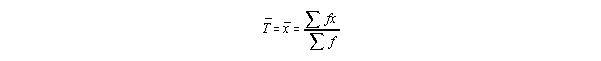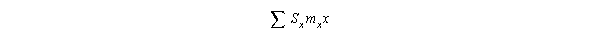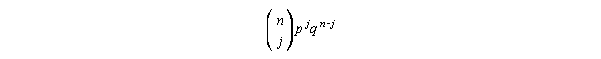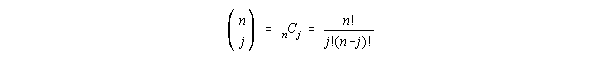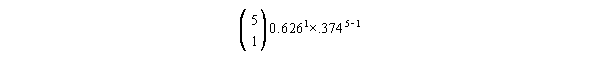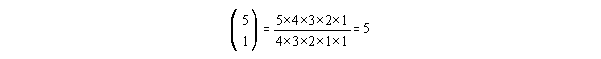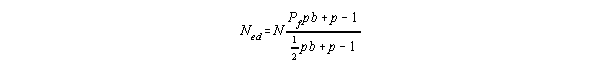More population ecology...
I. Generation length
What we're after here is some idea of how long a generation is. This is difficult
due to:
- differing time periods appropriate to different organisms (e.g., we can't
use the same time frame for fruit flies and elephants).
- we can't think in terms of individuals - we need to think in terms of
averages. (You might have brothers and sisters, but unless you're twins,
they won't be the same age, so what defines a "generation"?)
We look at the average age of mothers producing offspring during one season
(cycle) of births. This is: 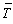 .
This is give as follows:
.
This is give as follows:
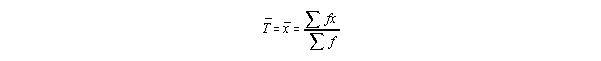
This says: Add up the ages in each category, and divide by the sample size (All
the denominator is, is "sample size". It's a short hand way of calculating the
sample mean. For example, normally we'd add up all the numbers and divide by
the sample size. Suppose we sort things instead:
Age 0 1 2 3
Number 5 6 4 7
We'd have to add five 0's, six 1's, four 2's, and seven 3's. Our formula gives us:
(0 x 5) + (1 x 6) + (2 x 4) + (3 x 7) = 0 + 6 + 8 + 21 = 33 (= numerator)
and
5 + 6 + 4 + 7 = 22 (= denominator)
so we have 33/22 = 1.5
The text then gives a way of getting this directly from life tables (see derivation
in text):
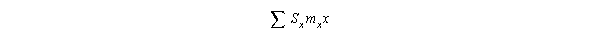
II. Stochastic effects
What we're after here is a realization that in small populations random effects are
much more important. (If, on average, half of a population of 10,000 dies before
age 10, that's not a big deal, but if we're dealing with a population of 8, then
hopefully it's obvious that we could easily wipe out all 8 before age 10).
We'll try to keep statistics to a minimum, though the text assumes quite a bit of
statistical knowledge (well, not that much, but it does assume you remember
everything from a introductory statistics class).
Skipping over the details, what we want is an idea of the probability of going
from one age bracket to the next. Using the text as an example (table 5.5), it lists
the survival from age 0 to 1 as 0.626. That means that about 63% of females
would survive to their first year.
- With a large population, the actual outcome is irrelevant (it's not real
important if we get 60% or 70% instead of 63%).
- But in this case, we have only 5 females. 63% would indicate that
roughly 3 survive to the next year.
- Obviously, though, we could get 0 survivals, or 5 survivals.
- If we toss a coin 5 times, we "expect" 2.5 heads (a little silly, but
mathematically true). But we could get 0 heads or 5 heads.
- So we want to calculate the probability of getting these other outcomes.
Let's use a slightly different approach than the book uses. We'll just jump
right in and use the binomial formula:
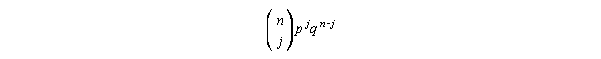
Now all we have to do is plug everything into this...
To explain, n = sample size, j = the number of survivors we're interested
in, p = survival rate, q = mortality rate. The prefix is as follows:
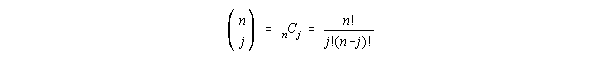
(n! = n factorial, = n x (n-1) x (n-2)...1, and by definition 0! = 1)
It's very easy to get bogged down in the details here, so we don't want to
spend too much time dissecting all this math. If you want to know more,
look up the binomial in your stats book or come see me. So let's see
where that leaves us.
- Suppose now we want to calculate the probability of only 1
female surviving to age 1. We plug everything into our equation,
and we get:
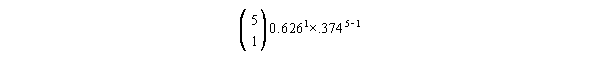
The prefix is:
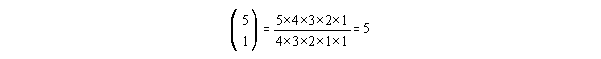
(cancel the similar terms - don't try to solve this by hitting the
factorial button).
The rest of the equation is simple to solve on a calculator, and
gives us 0.01224787, we multiply this by 5 to get 0.061239.
Important: the text made a mistake here. For whatever reason,
they're using p = .6558 instead of p = .626.
- The probability of getting 3 females surviving is 0.343.
- This is kind of low. Although this is what happened, the
probability is only about 34% (there's a 66% probability
that something else will happen)
- The probability of getting NO survivors is 0.7 % (small,
but not impossible).
- With small populations, random effects are important.
- The rest of this section is not that important (it deals with the
spread (variance) of things and a couple of other related concepts).
- But note that r is also affected by these random changes (that's a
good part of the point made in the rest of the section).
III. Metapopulations
- We'll also ignore this section for now. We may get back to it if there's time.
More on stochastic (= random) effects.
As should be obvious from the discussion to this point, small populations are more
strongly affected by random effects. If a population is small, it might die out just due to
random chance.
There are two reasons to be particularly concerned with small populations:
1) The population size can swing erratically from season to season.
2) Since there is population size is small, there is no buffer should the population
swing too low.
Given birth and death rates, as well as r and initial population size, the probability of a
population dying out within a specified interval (t) can be calculated. See formula on
page 167 if interested.
I. Effective population size
The size of a population may not be the best indicator as to rates of increase or
decrease. At small populations, interesting things can happen. For example,
- St. Matthew Island reindeer crashed after exhausting food supply. There
were just over 30 females left, and one male.
- normally, this would be cause for concern, but notice that the sex
ratio is not 50:50. There are far more females available. Thus, it
is quite conceivable that this population might have grown faster.
- Unfortunately, stupidity intervened, and a few specimens
were shot to try and gauge the condition of the herd. The
male was accidentally shot.
One can compare this "enhanced" growth with a normal population and
determine the size of this normal population that would achieve the same growth.
This is the concept of "effective population size". Without too much discussion
of the derivation (see text for details, if interested) we arrive at:
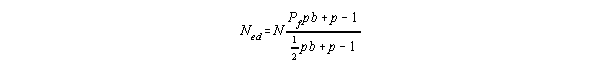
Here Ned = effective population size, N = population size, Pf = proportion of
females, p = probability of surviving the following year (averaged out over all
ages), and b = number of live births per female this year.
- This has been just slightly re-written with the N off to the side.
- This makes it a little more intuitive as to what's happening. Notice that
the fraction can be greater or less than 1. If it's greater, then Ned is larger
than N (i.e., that's good - a smaller population is growing faster), if it's
less, then Ned is less than N (bad, a smaller population is growing slower).
- if the proportion of females (Pf) = 1/2, then obviously both the numerator
and denominator will be the same, and there is no difference between N
and Ned. If Pf > 1/2, there are more females, and the fraction will be
greater than 1, and vice-versa.
- so this is a way of quantifying the reindeer example
- the text gives further details, including how to derive Ned directly from life
tables.
II. Random environmental effects
Simply, the effects of these on populations.
This has a rather different effect than that due to small population size. A
drought, for example, can hit all animals in a population equally. Often, the
proportion of animals affected remains the same regardless of population size.
- However, it seems obvious a large population might not survive a
drought as well as a smaller population (there might be more than enough
food and water for a smaller population). The text doesn't seem to go into
this.
- We shouldn't differentiate between large scale disasters and small scale
disasters. Both have an impact on our population.
One of the main interests here is persistence of a population. Given the above, it
should not be surprising that the exact effect that random environmental effects
have vary with the species. In particular, how the rate of increase interacts with
the environmental variability is important.
- We'll simply note that very few species behave exactly as predicted by
these equations.
- Most of these models predict a population growth near zero as a
population approaches K.
- K is defined as carrying capacity, but often in practice (in the field) it is
hard to quantify K. See the quote by Pimm on page 172 (basically, he
notes that most populations are only at about « K).
III. Loss of Social structure
(We're temporarily skipping over the genetic stuff - we'll do that in the next set
of notes - let's just finish the rest of chapter 6)
An important point not often considered.
Many animals may have certain social behaviors that are essential to their
survival.
Reproduction I - e.g., leks, were males strut around to compete for
females. Suppose there are only one or two males available - would
females still be attracted?
Reproduction II - colonial breeders depend on living in groups. Similarly,
animals living in groups may have a much easier time finding a mate.
Group foraging - if a species is dependant on finding a certain type of
(patchy) food, this is greatly eased by having many individuals look for
the food. The text cites passenger pigeons as an example (looking for
mast crops).
Herd behavior - safety in numbers. If numbers drop too low, this may no
longer work.
Cooperative hunting - some predators (e.g. lions) hunt in groups, and
would be considerably less effective hunting alone.
- African hunting dogs or wolves hunt in packs - often their
strategy is to "run down" their prey until it is exhausted. This
obviously requires many individuals working together.
Defense - bees and wasps are considerably more effective in swarms than
as single units. In the case of bees (and some wasps), the entire social
system is dependant on a certain minimum size to be effective.
Numerous other examples can be enumerated.
It is important to realize that loss of social structure can have devastating effects
on the population under consideration.
IV. Minimum Viable population size
A lot of the previous topics (and genetics which we'll discuss next time) boils
down to this: at what stage is a population too small to survive? What is a
"minimum viable population"?
- Fortunately, there are numerous examples where with only a few
individuals (e.g., black robin, where there was only one female left) the
population recovered. But without intervention, it would most likely have
crashed.
- The best way to think about this might be as follows:
(Simberloff): "the size below which rapid extinction is likely"
We've discussed the problems with small population sizes, so it
should be obvious that the smaller a population, the more likely it
is to become extinct simply doe these random factors.
- Its not really possible to put a number on this (except for the obvious sort
of "no males and only one female left").
- But we can think of it kind of when the factors we looked at in this
chapter (we haven't looked at the genetics yet!) become increasingly
important to the survival (or lack thereof) of the population.
V. Some comments on what's next
- Genetics - we already discussed this.
- We'll start using these concepts to try and figure out, for example, what is the
minimum size of reserves for a population to survive, and similar things. Chapter
7 deals with some of these concepts (and is also the last really mathematical
chapter).
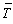 .
This is give as follows:
.
This is give as follows:
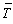 .
This is give as follows:
.
This is give as follows: