Project 4: Laplace
Team members: Brendan Gramp, Aidan Curran, Eadom Dessalene
Contents
Background
Check code by reproducing the results of Example 8.8. Warmup exercise: Computer Problem 8.3.6. Main problem: Exercise 8.3.13 plus Computer Problem 8.3.18(a).
Example 8.8
poisson_ex(0,1,1,2,5,5)
ans =
0 0.3646 0.6729 0.9400 1.1756 1.3863
0.0392 0.3916 0.6927 0.9552 1.1876 1.3962
0.1484 0.4697 0.7510 1.0003 1.2236 1.4255
0.3075 0.5878 0.8415 1.0714 1.2808 1.4725
0.4947 0.7325 0.9556 1.1631 1.3558 1.5347
0.6931 0.8920 1.0852 1.2698 1.4446 1.6094
Warmup 8.3.6
The steady-state temperature u on a heated copper plate satisfies the Poisson equation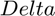 
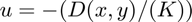where D(x,y) is the power density at (x,y) and K is the thermal conductivity. Assume that the plate is the shape of the rectangle [0, 4] x [0, 2] cm whose boundary is kept at a constant 30 degrees C, and that power is generated at the constant rate D(x,y) = 5 watts/cm3. The thermal conductivity of copper is K = 3.85 watts/cm Degrees C.
(a) Plot the temperature distribution on the plate.
a = poisson_6(0,4,0,2,20,20)
a = Columns 1 through 7 30.0000 30.0000 30.0000 30.0000 30.0000 30.0000 30.0000 30.0000 30.0406 30.0723 30.0975 30.1177 30.1337 30.1462 30.0000 30.0649 30.1187 30.1633 30.1999 30.2295 30.2529 30.0000 30.0811 30.1504 30.2091 30.2582 30.2984 30.3305 30.0000 30.0924 30.1726 30.2415 30.2997 30.3479 30.3866 30.0000 30.1004 30.1883 30.2645 30.3293 30.3834 30.4270 30.0000 30.1060 30.1994 30.2807 30.3503 30.4085 30.4557 30.0000 30.1098 30.2070 30.2918 30.3647 30.4258 30.4755 30.0000 30.1123 30.2119 30.2991 30.3741 30.4371 30.4883 30.0000 30.1137 30.2147 30.3032 30.3793 30.4434 30.4956 30.0000 30.1142 30.2156 30.3045 30.3811 30.4455 30.4979 30.0000 30.1137 30.2147 30.3032 30.3793 30.4434 30.4956 30.0000 30.1123 30.2119 30.2991 30.3741 30.4371 30.4883 30.0000 30.1098 30.2070 30.2918 30.3647 30.4258 30.4755 30.0000 30.1060 30.1994 30.2807 30.3503 30.4085 30.4557 30.0000 30.1004 30.1883 30.2645 30.3293 30.3834 30.4270 30.0000 30.0924 30.1726 30.2415 30.2997 30.3479 30.3866 30.0000 30.0811 30.1504 30.2091 30.2582 30.2984 30.3305 30.0000 30.0649 30.1187 30.1633 30.1999 30.2295 30.2529 30.0000 30.0406 30.0723 30.0975 30.1177 30.1337 30.1462 30.0000 30.0000 30.0000 30.0000 30.0000 30.0000 30.0000 Columns 8 through 14 30.0000 30.0000 30.0000 30.0000 30.0000 30.0000 30.0000 30.1556 30.1621 30.1660 30.1673 30.1660 30.1621 30.1556 30.2706 30.2830 30.2903 30.2928 30.2903 30.2830 30.2706 30.3549 30.3721 30.3824 30.3858 30.3824 30.3721 30.3549 30.4163 30.4373 30.4498 30.4539 30.4498 30.4373 30.4163 30.4606 30.4844 30.4986 30.5033 30.4986 30.4844 30.4606 30.4921 30.5179 30.5334 30.5385 30.5334 30.5179 30.4921 30.5138 30.5411 30.5575 30.5629 30.5575 30.5411 30.5138 30.5280 30.5562 30.5731 30.5788 30.5731 30.5562 30.5280 30.5360 30.5648 30.5820 30.5877 30.5820 30.5648 30.5360 30.5386 30.5675 30.5848 30.5906 30.5848 30.5675 30.5386 30.5360 30.5648 30.5820 30.5877 30.5820 30.5648 30.5360 30.5280 30.5562 30.5731 30.5788 30.5731 30.5562 30.5280 30.5138 30.5411 30.5575 30.5629 30.5575 30.5411 30.5138 30.4921 30.5179 30.5334 30.5385 30.5334 30.5179 30.4921 30.4606 30.4844 30.4986 30.5033 30.4986 30.4844 30.4606 30.4163 30.4373 30.4498 30.4539 30.4498 30.4373 30.4163 30.3549 30.3721 30.3824 30.3858 30.3824 30.3721 30.3549 30.2706 30.2830 30.2903 30.2928 30.2903 30.2830 30.2706 30.1556 30.1621 30.1660 30.1673 30.1660 30.1621 30.1556 30.0000 30.0000 30.0000 30.0000 30.0000 30.0000 30.0000 Columns 15 through 21 30.0000 30.0000 30.0000 30.0000 30.0000 30.0000 30.0000 30.1462 30.1337 30.1177 30.0975 30.0723 30.0406 30.0000 30.2529 30.2295 30.1999 30.1633 30.1187 30.0649 30.0000 30.3305 30.2984 30.2582 30.2091 30.1504 30.0811 30.0000 30.3866 30.3479 30.2997 30.2415 30.1726 30.0924 30.0000 30.4270 30.3834 30.3293 30.2645 30.1883 30.1004 30.0000 30.4557 30.4085 30.3503 30.2807 30.1994 30.1060 30.0000 30.4755 30.4258 30.3647 30.2918 30.2070 30.1098 30.0000 30.4883 30.4371 30.3741 30.2991 30.2119 30.1123 30.0000 30.4956 30.4434 30.3793 30.3032 30.2147 30.1137 30.0000 30.4979 30.4455 30.3811 30.3045 30.2156 30.1142 30.0000 30.4956 30.4434 30.3793 30.3032 30.2147 30.1137 30.0000 30.4883 30.4371 30.3741 30.2991 30.2119 30.1123 30.0000 30.4755 30.4258 30.3647 30.2918 30.2070 30.1098 30.0000 30.4557 30.4085 30.3503 30.2807 30.1994 30.1060 30.0000 30.4270 30.3834 30.3293 30.2645 30.1883 30.1004 30.0000 30.3866 30.3479 30.2997 30.2415 30.1726 30.0924 30.0000 30.3305 30.2984 30.2582 30.2091 30.1504 30.0811 30.0000 30.2529 30.2295 30.1999 30.1633 30.1187 30.0649 30.0000 30.1462 30.1337 30.1177 30.0975 30.0723 30.0406 30.0000 30.0000 30.0000 30.0000 30.0000 30.0000 30.0000 30.0000
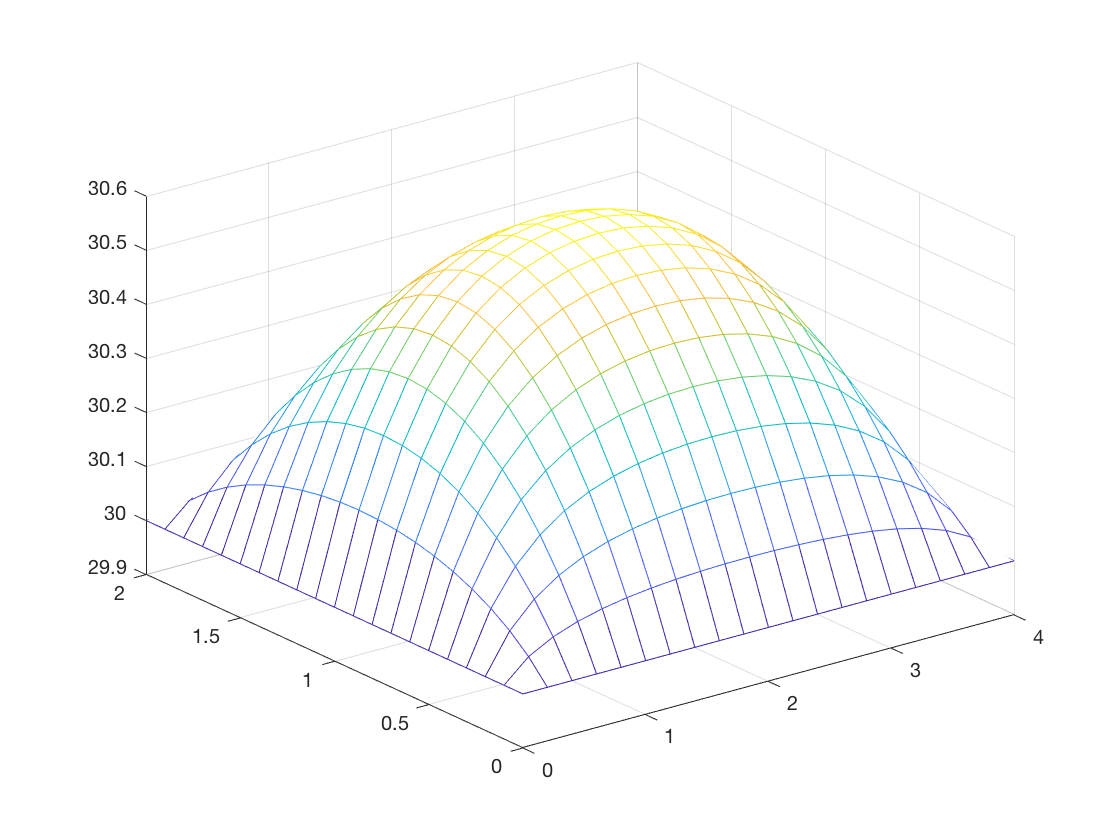
(b) Find the temperature, at the center point (x,y) = (2,1).
The code estimates the temperature value at (2,1) to be
a(11,11)
ans = 30.5906
Exercise 8.3.13
Question
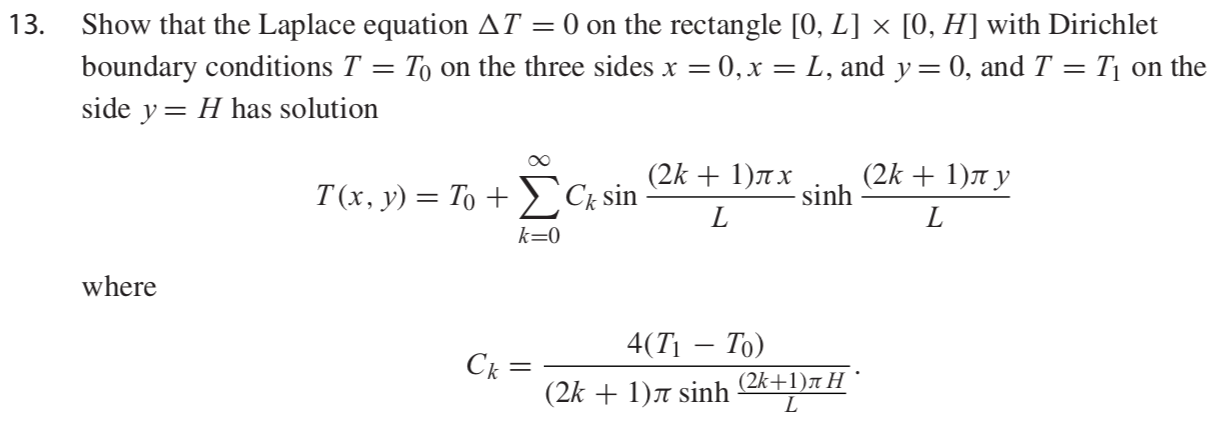
Work
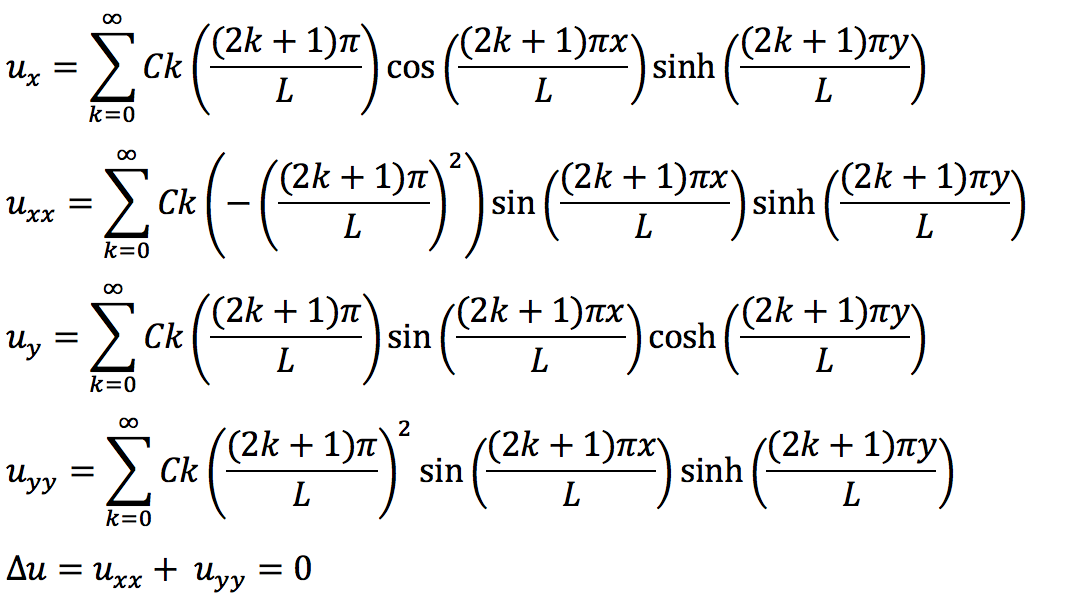
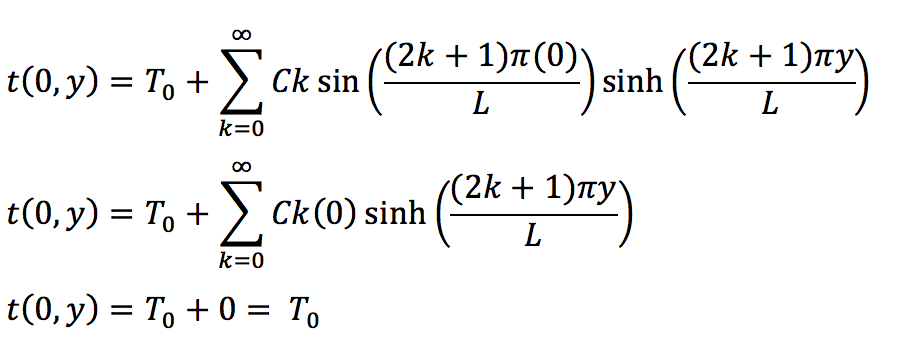
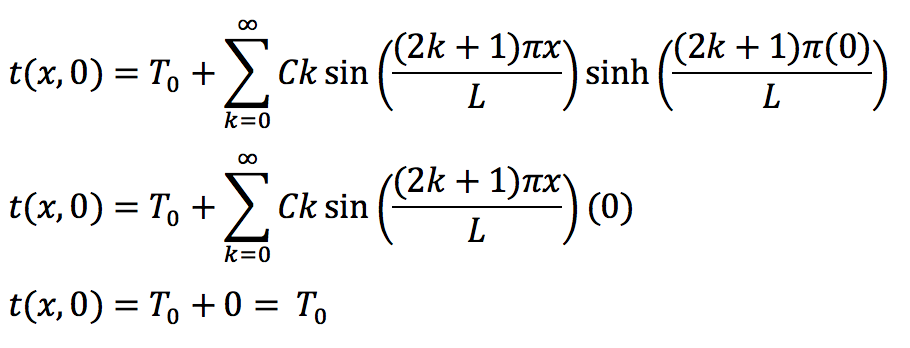
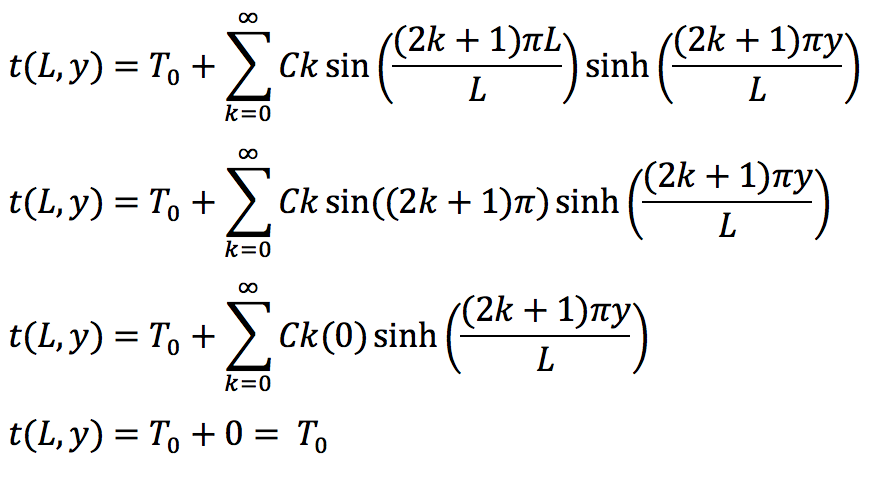
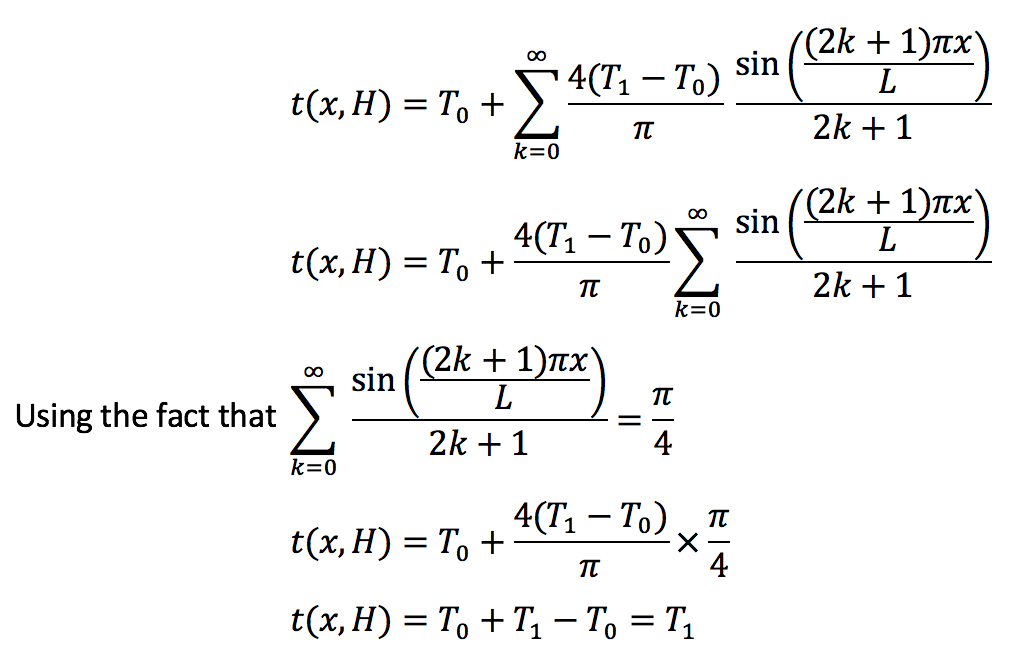
Computer Problem 8.3.18 (a)
Solve the Laplace equation with Dirichlet boundary conditions from Exercise 13 on [0, 1] × [0, 1] with T0 = 0 and T1 = 10 using (a) a finite difference approximation Make log-log plots of the error at particular locations in the rectangle as a function of step sizes h = k = 2^-p for p as large as possible. Explain any simplifications you are making to evaluate the correct solution at those locations.
f=@(x,y) 0;
g1=@(x) 0;
g2=@(x) 10;
g3=@(y) 0;
g4=@(y) 0;Code used: K Error Code, Log to List Code, Dirichlet Code
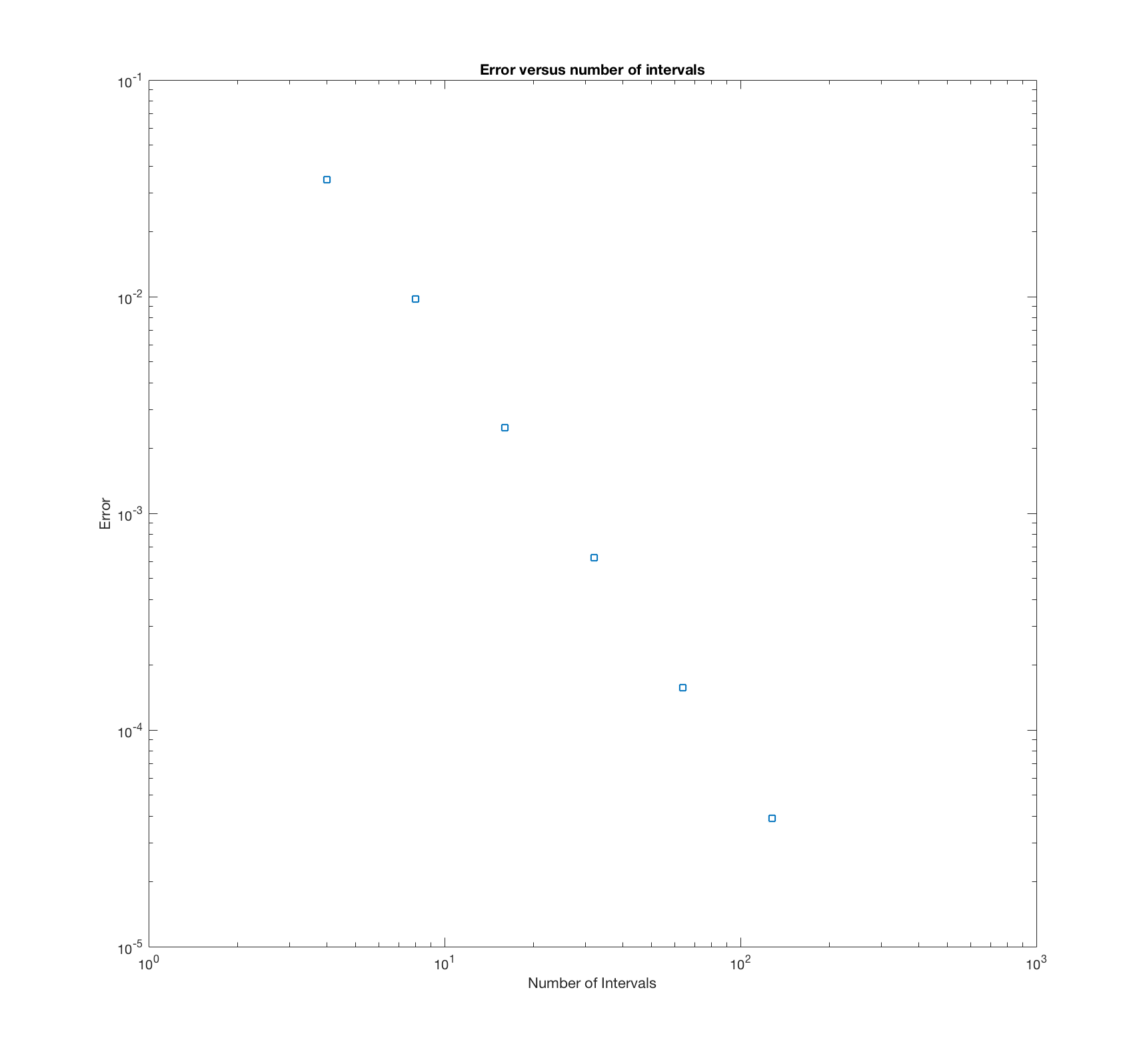
kError(1/4,1/4)
init =
4
t =
0 0 0 0 0 0
t =
4 0 0 0 0 0
t =
4 8 0 0 0 0
t =
4 8 16 0 0 0
t =
4 8 16 32 0 0
t =
4 8 16 32 64 0
t =
4 8 16 32 64 128
error =
0.0346
error =
0.0346
x =
0.0346 0 0 0 0 0
error =
0.0098
error =
0.0098
x =
0.0346 0.0098 0 0 0 0
error =
0.0025
error =
0.0025
x =
0.0346 0.0098 0.0025 0 0 0
error =
6.2621e-04
error =
6.2621e-04
x =
0.0346 0.0098 0.0025 0.0006 0 0
error =
1.5672e-04
error =
1.5672e-04
x =
0.0346 0.0098 0.0025 0.0006 0.0002 0
error =
3.9191e-05
error =
3.9191e-05
x =
0.0346 0.0098 0.0025 0.0006 0.0002 0.0000
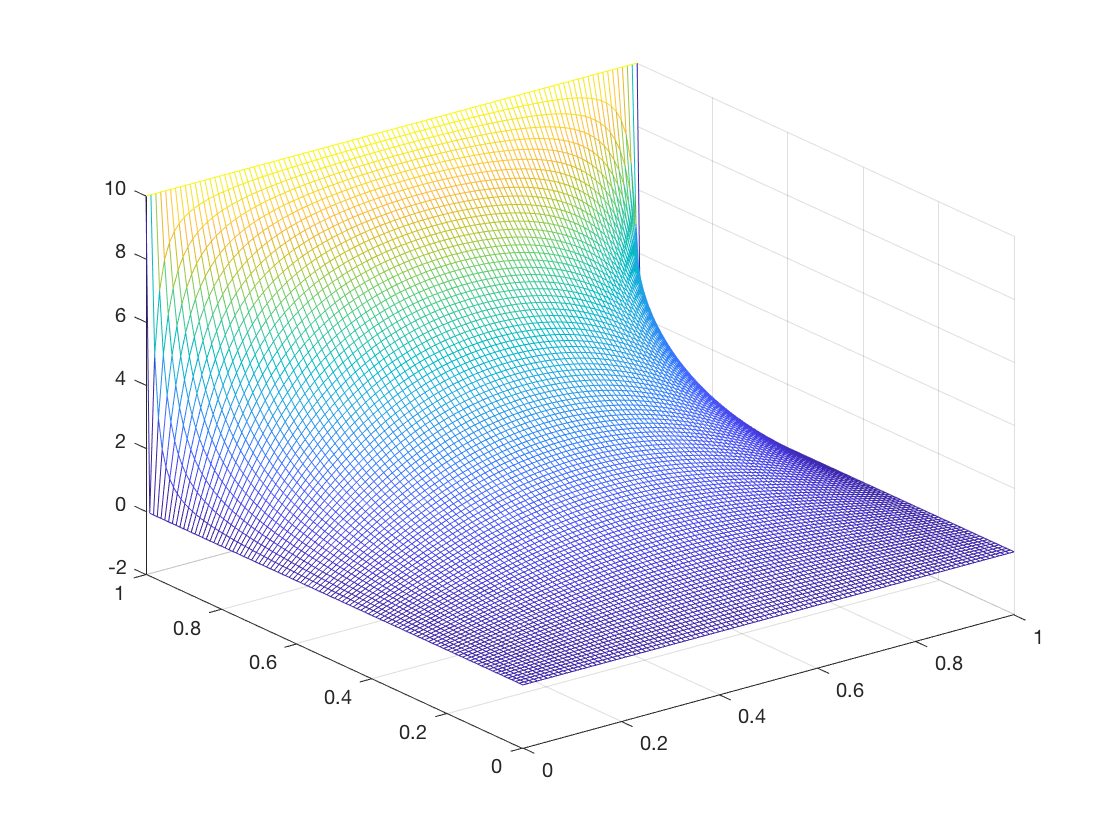
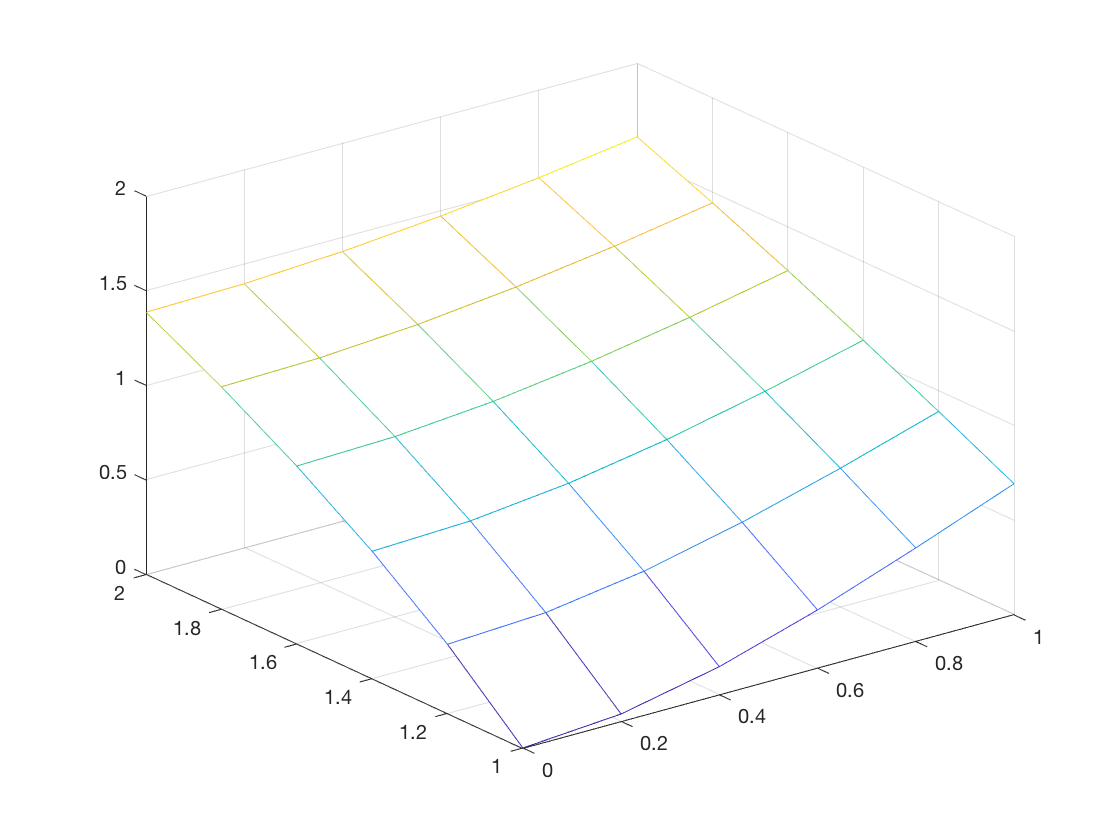
kError(1/4,1/2)
init =
4
t =
0 0 0 0 0 0
t =
4 0 0 0 0 0
t =
4 8 0 0 0 0
t =
4 8 16 0 0 0
t =
4 8 16 32 0 0
t =
4 8 16 32 64 0
t =
4 8 16 32 64 128
error =
0.0547
error =
0.0547
x =
0.0547 0 0 0 0 0
error =
0.0180
error =
0.0180
x =
0.0547 0.0180 0 0 0 0
error =
0.0049
error =
0.0049
x =
0.0547 0.0180 0.0049 0 0 0
error =
0.0012
error =
0.0012
x =
0.0547 0.0180 0.0049 0.0012 0 0
error =
3.1301e-04
error =
3.1301e-04
x =
0.0547 0.0180 0.0049 0.0012 0.0003 0
error =
7.8354e-05
error =
7.8354e-05
x =
0.0547 0.0180 0.0049 0.0012 0.0003 0.0001
